Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Hà Nam có đáp án

1.Rút gọn biểu thức \(A = 2\sqrt 3  - 3\sqrt {27}  + 7\sqrt {7 + 4\sqrt 3 } .\)

\(A = 2\sqrt 3  - 9\sqrt 3  + 7\sqrt {{{\left( {2 + \sqrt 3 } \right)}^2}} \)

\(A = 2\sqrt 3  - 9\sqrt 3  + 7\left( {2 + \sqrt 3 } \right)\)

\(A = 14\)

2.  Cho biểu thức \(P = \frac{1}{{2\sqrt x  - 4}} - \frac{1}{{2\sqrt x  + 4}} + \frac{{\sqrt x }}{{x - 4}}\) (với \(x \ge 0,\,x \ne 4\) ).

a) Rút gọn biểu thức \(P.\)

\(P = \frac{8}{{4x - 16}} + \frac{{\sqrt x }}{{x - 4}}\)

\(P = \frac{{\sqrt x  + 2}}{{x - 4}} = \frac{1}{{\sqrt x  - 2}}\)

b) Tìm tất cả các số nguyên \(x\) để \(P\) đạt giá trị nguyên.

\(P\) đạt giá trị nguyên \( \Leftrightarrow \sqrt x  - 2 =  \pm 1\)

\(\sqrt x  - 2 = 1 \Leftrightarrow \sqrt x  = 3 \Leftrightarrow x = 9\)(thỏa mãn điều kiện \(x \ge 0,\,x \ne 4\)).

\(\sqrt x  - 2 =  - 1 \Leftrightarrow \sqrt x  = 1 \Leftrightarrow x = 1\)(thỏa mãn điều kiện \(x \ge 0,\,x \ne 4\)).

1.  Giải phương trình \({x^2} + 2x - 15 = 0.\)

\(\Delta ' = 1 + 15 = 16 > 0\) .

Phương trình có hai nghiệm phân biệt

\({x_1} =  - 1 + \sqrt {16}  = 3\) .

\({x_2} =  - 1 - \sqrt {16}  =  - 5\).

2.  Giải hệ phương trình \(\left\{ \begin{array}{l}x\left( {4 - 2y} \right) = 7 + y - 2xy\\2x - 14 = 2\left( {y - 3} \right)\end{array} \right..\)

\(\left\{ \begin{array}{l}x\left( {4 - 2y} \right) = 7 + y - 2xy\\2x - 14 = 2\left( {y - 3} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - y = 7\\2x - 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - y = 7\\x - y = 4\end{array} \right.\).

\( \Leftrightarrow \left\{ \begin{array}{l}3x = 3\\x - y = 4\end{array} \right.\).

\( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 3\end{array} \right.\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1; - 3} \right)\).

1.\((d) \bot \left( \Delta  \right) \Leftrightarrow 2.\left( {a - 3} \right) =  - 1\)

\( \Leftrightarrow a = \frac{5}{2}\).

2.Phương trình hoành độ giao điểm của đường thẳng \((d)\)và \((P)\,\)

\({x^2} = 2x + {m^2} - 4m + 9 \Leftrightarrow {x^2} - 2x - {m^2} + 4m - 9 = 0\,\left( 1 \right)\)

\(\Delta ' = {m^2} - 4m + 10 = {\left( {m - 2} \right)^2} + 6 > 0\,\forall m\)

Vậy đường thẳng \((d)\)luôn cắt \((P)\,\)tại hai điểm phân biệt \(A,\,B\) với mọi \(m\)

\(a.c =  - {m^2} + 4m - 9 =  - {\left( {m - 2} \right)^2} - 5 < 0\,\forall m \Rightarrow \) Phương trình \(\left( 1 \right)\) luôn có hai nghiệm trái dấu \({x_1} < 0 < {x_2}\)

\(\left\{ \begin{array}{l}{x_1} - 2023 < 0\\{x_2} + 2023 > 0\end{array} \right. \Rightarrow \left| {{x_1} - 2023} \right| - \left| {{x_2} + 2023} \right| =  - \left( {{x_1} + {x_2}} \right)\)

\[\begin{array}{l}\left| {{x_1} - 2023} \right| - \left| {{x_2} + 2023} \right| = {y_1} + {y_2} - 48 \Leftrightarrow  - \left( {{x_1} + {x_2}} \right) = x_1^2 + x_2^2 - 48\\ \Leftrightarrow  - \left( {{x_1} + {x_2}} \right) = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} - 48 \Leftrightarrow  - 2 = {2^2} - 2\left( { - {m^2} + 4m - 9} \right) - 48\\ \Leftrightarrow {m^2} - 4m - 12 = 0 \Rightarrow \left[ \begin{array}{l}m = 6\\m =  - 2\end{array} \right..\end{array}\]

1.\(DC \bot AD \Rightarrow \widehat {ADC} = 90^\circ \) .

\(AE \bot EC \Rightarrow \widehat {AEC} = 90^\circ \).

\(\widehat {ADC} + \widehat {AEC} = 180^\circ \).

\( \Rightarrow \) Tứ giác \(AECD\) nội tiếp đường tròn..

2.Tứ giác \(AECD\) nội tiếp \( \Rightarrow \widehat {CDE} = \widehat {CAE}.\).

\(\widehat {CDB} + \widehat {CFB} = 180^\circ  \Rightarrow \)Tứ giác \(CDBF\) nội tiếp \( \Rightarrow \widehat {CFD} = \widehat {CBD}.\).

Mà \(\widehat {CBD} = \widehat {CAE}\) ( Cùng chắn cung \(AC\) ).

\( \Rightarrow \widehat {CDE} = \widehat {CFD}.\).

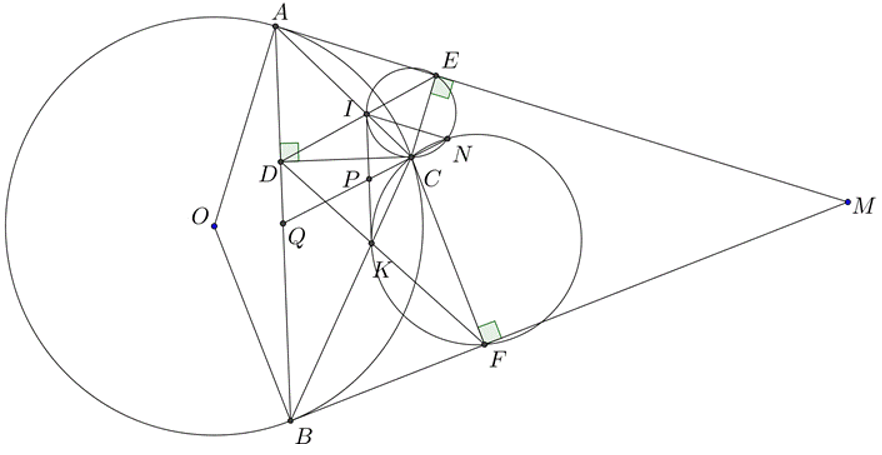
3.Tứ giác \(CDBF\) nội tiếp \( \Rightarrow \widehat {CFD} = \widehat {CBD}.\)

\(\widehat {CDE} = \widehat {CFD}\)(Chứng minh trên)

\( \Rightarrow \) \(\widehat {CDE} = \widehat {CBD}\) hay \(\widehat {CDI} = \widehat {CBA}\,\left( 1 \right)\)

Tứ giác \(CDBF\) nội tiếp \(\widehat {CDF} = \widehat {CBF}\)

Mà \(\widehat {CBF} = \widehat {CAB}\) (Cùng chắn cung \(BC\))

 \( \Rightarrow \widehat {CDK} = \widehat {CAB}\,\left( 2 \right)\).

Từ \(\left( 1 \right),\,\left( 2 \right) \Rightarrow \widehat {ICK} + \widehat {IDK} = \widehat {ICK} + \widehat {IDC} + \widehat {CDK}\)=\(\widehat {ACB} + \widehat {CBA} + \widehat {CAB} = {180^0}\)

\( \Rightarrow \) Tứ giác \(CIDK\) nội tiếp.

Suy ra \(\widehat {CIK} = \widehat {CDK}\)

Mà  \(\widehat {CDK} = \widehat {CAB}\,\)(Chứng minh trên)

\( \Rightarrow \widehat {CIK} = \widehat {CAB}\).

\( \Rightarrow IK\) //\(AB\)

Mà \(CD \bot AB \Rightarrow CD \bot IK.\).

4.Gọi \(NC\) cắt \(IK,\,AB\) lần lượt tại \(P,\,Q\)

\(\widehat {CIK} = \widehat {CAB}\) (Chứng minh trên).

Tứ giác \(AECD\) nội tiếp đường tròn \( \Rightarrow \widehat {CAD} = \widehat {CED}\) hay \(\widehat {CAB} = \widehat {CEI}\)

\( \Rightarrow \widehat {CEI} = \widehat {CIK}\)

\( \Rightarrow IK\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(CIE\)

Chứng minh tương tự: \(IK\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(CKF\) .

Xét hai tam giác \(PIC,\,PNI\) có

\(\widehat {IPN}\) chung, \(\widehat {PIC} = \widehat {PNI}\) (cùng chắn cung \(IC\))

 .

\( \Rightarrow \frac{{PI}}{{PN}} = \frac{{PC}}{{PI}} \Rightarrow P{I^2} = PC.PN\)

Chứng minh tương tự: \(P{K^2} = PC.PN\)

Vậy \(PI = PK\) .

\(IK\) // \(AB\) \( \Rightarrow \frac{{IP}}{{AQ}} = \frac{{CP}}{{CQ}} = \frac{{PK}}{{QB}}\)

Mà \(PI = PK \Rightarrow AQ = QB\)

Hay \(Q\) là trung điểm của \(AB\) .

Ta có:

\[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  = \sqrt {2022a + \frac{{{{\left( {b + c} \right)}^2}}}{2} - 2bc}  \le \sqrt {2022a + \frac{{{{\left( {b + c} \right)}^2}}}{2}} \]  (vì bc ≥ 0)

Þ \[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  \le \sqrt {2022a + \frac{{{{\left( {1011 - a} \right)}^2}}}{2}} \]

Þ \[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  \le \sqrt {\frac{{{{\left( {1011 + a} \right)}^2}}}{2}} \]

Þ \[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  \le \frac{{1011 + a}}{{\sqrt 2 }}\]  dấu = xảy ra  Û \[\left\{ \begin{array}{l}bc = 0\\a + b + c = 1011\end{array} \right.\]

Tương tự:      \[\sqrt {2022b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  \le \frac{{1011 + b}}{{\sqrt 2 }}\]

                     \[\sqrt {2022c + \frac{{{{\left( {c - b} \right)}^2}}}{2}}  \le \frac{{1011 + c}}{{\sqrt 2 }}\]       

\[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {2022b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {2022c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le \frac{{3.1011 + a + b + c}}{{\sqrt 2 }}\]

Þ\[\sqrt {2022a + \frac{{{{\left( {b - c} \right)}^2}}}{2}}  + \sqrt {2022b + \frac{{{{\left( {c - a} \right)}^2}}}{2}}  + \sqrt {2022c + \frac{{{{\left( {a - b} \right)}^2}}}{2}}  \le \frac{{4.1011}}{{\sqrt 2 }} = 2022\sqrt 2 \]

Dấu = xảy ra Û \[\left\{ \begin{array}{l}a + b + c = 1011\\ab = bc = ca = 0\end{array} \right.\]

(Khi trong ba số \(a,\,b,\,c\) có một số bằng 1011 và hai số bằng 0).