Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 35

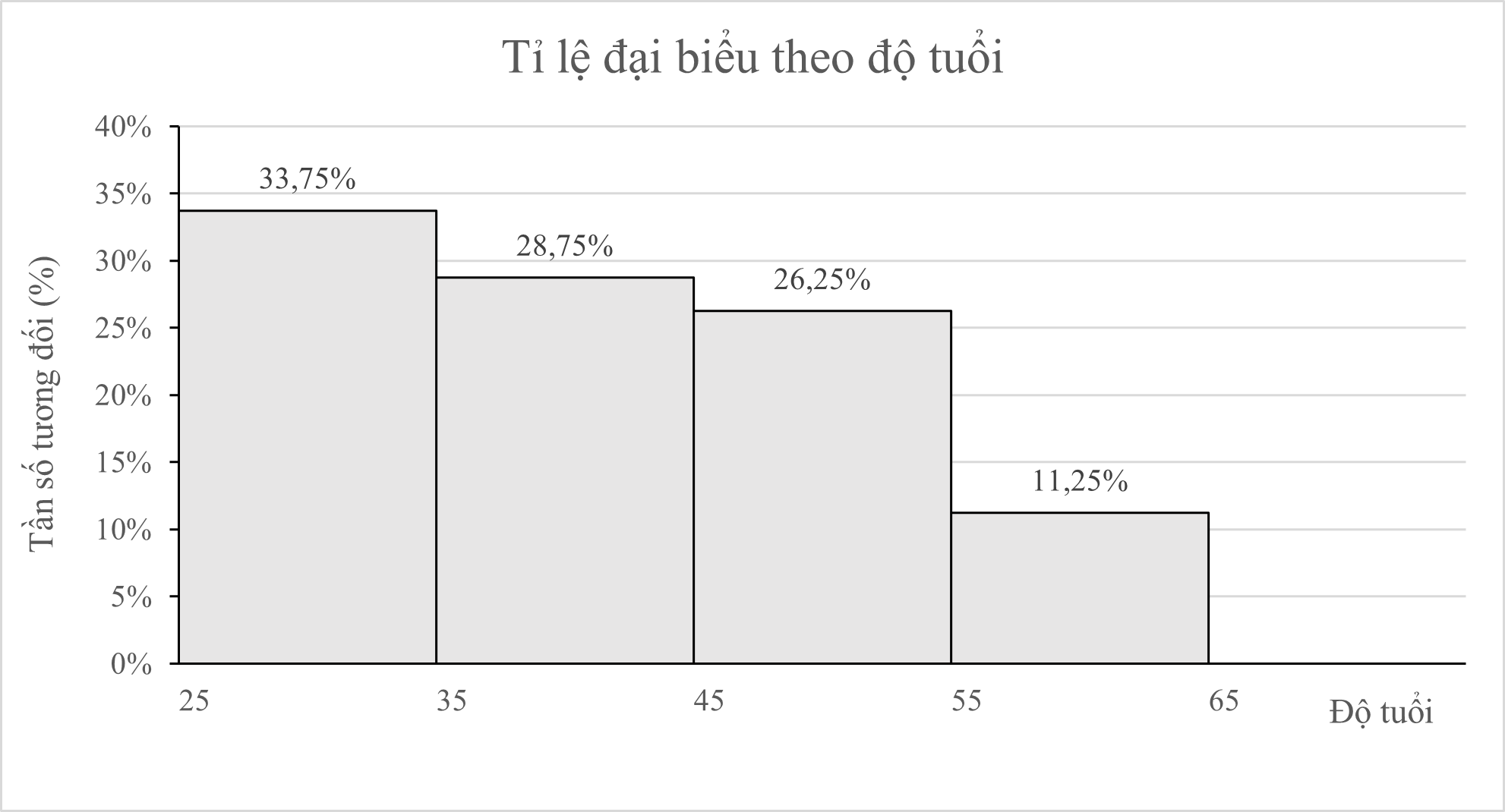
a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.

Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)

Vậy tổng số đại biểu tham dự hội nghị là 160 người.

b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:

\[33,75\%  + 28,75\%  = 62,5\%  > 50\% .\]

Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.

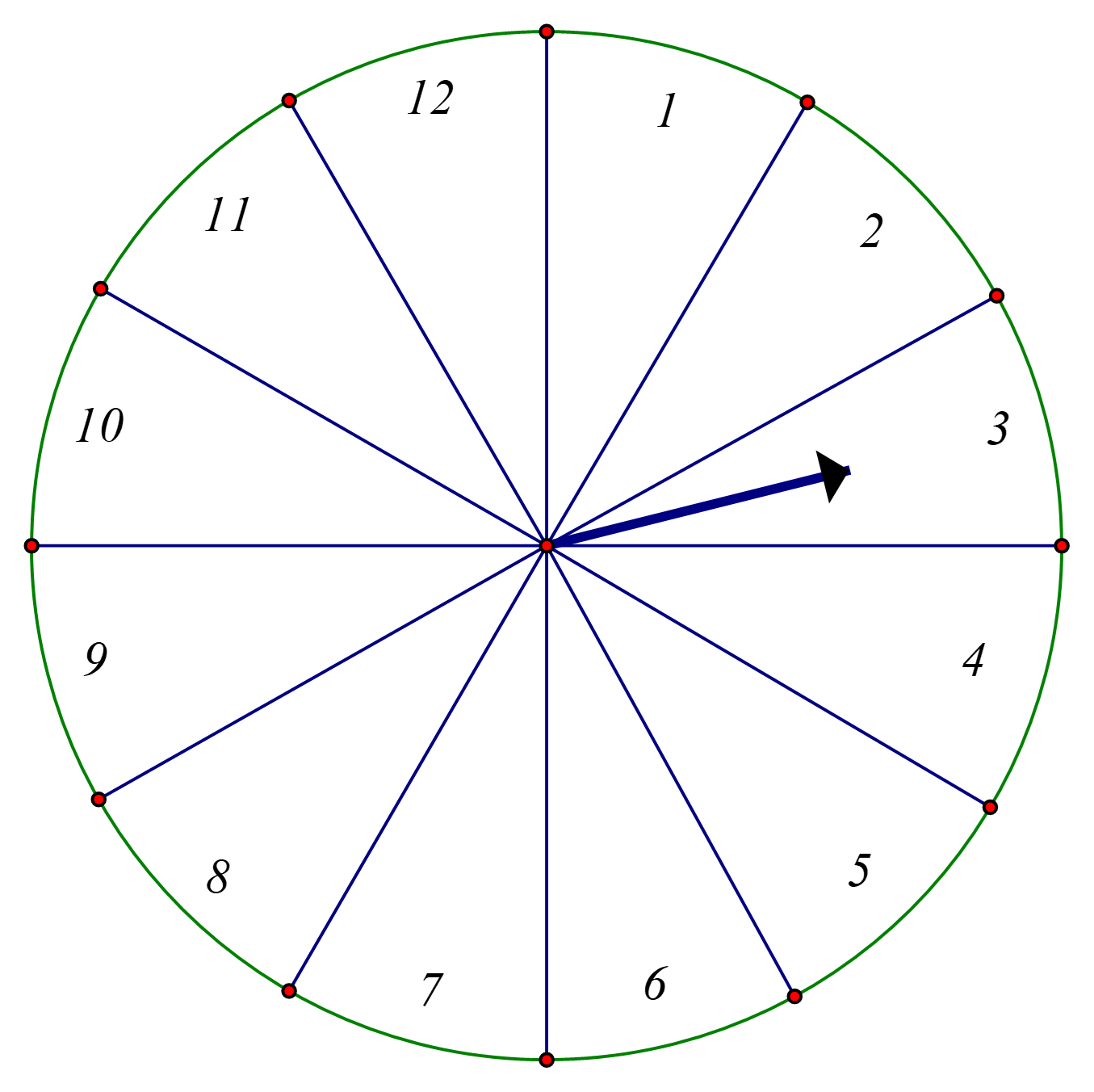
Có \[12\] kết quả có thể xảy ra khi quay ngẫu nhiên tấm bìa một lần.

\[A = \left\{ {1;\,\,2;\,\,3;\,\,...\,\,;\,\,12} \right\}\]

Có \[5\] kết quả thuận lợi cho biến cố B là: \[2;\,\,3;\,\,5;\,\,7;\,\,11 & \].

Vậy xác suất của biến \[P\] cố là: \[\frac{5}{{12}}\].

a) Thay \[x = 4\] (thỏa mãn điều kiện) vào biểu thức \[A\] ta có: \(A = \frac{{\sqrt 4  + 1}}{{\sqrt 4  + 3}} = \frac{3}{5}\)  

        Vậy giá trị của biểu thức \(A\) tại \(x = 4\) là: \(\frac{3}{5}\)

                        b)  Ta có: \(B = \frac{{2\sqrt x }}{{\sqrt x  + 1}} - \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}} + \frac{{2\sqrt x  + 4}}{{x - 1}}\)

\[ = \frac{{2\sqrt x }}{{\sqrt x  + 1}} - \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}} + \frac{{2\sqrt x  + 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{2\sqrt x \left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} - \frac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \frac{{2\sqrt x  + 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{2\sqrt x \left( {\sqrt x  - 1} \right) - \left( {\sqrt x  + 2} \right)\left( {\sqrt x  + 1} \right) + 2\sqrt x  + 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{2x - 2\sqrt x  - x - 2\sqrt x  - \sqrt x  - 2 + 2\sqrt x  + 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{x - 3\sqrt x  + 2}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\]

\[ = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}}\]

                        Vậy \[B = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}}\] với \(x \ge 0;x \ne 1\).

        c) Ta có: \(A.B \le \frac{1}{2}\)

                         \(\frac{{\sqrt x  + 1}}{{\sqrt x  + 3}} \cdot \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}} \le \frac{1}{2}\)

                                        \(\frac{{\sqrt x  - 2}}{{\sqrt x  + 3}} \le \frac{1}{2}\)

                                 \(\frac{{\sqrt x  - 2}}{{\sqrt x  + 3}} - \frac{1}{2} \le 0\)

                     \(\frac{{2\sqrt x  - 4 - \sqrt x  - 3}}{{2\left( {\sqrt x  + 3} \right)}} \le 0\)

                                 \(\frac{{\sqrt x  - 7}}{{2\left( {\sqrt x  + 3} \right)}} \le 0\)

                                 \(\sqrt x  - 7 \le 0\)  (Vì \(2\left( {\sqrt x  + 3} \right) > 0\))

\(\sqrt x  \le 7\)

\(x \le 49\)

                 Kết hợp điều kiện ta có: \(0 \le x \le 49;\,\,\,x \ne 1\).

                 Vậy \(0 \le x \le 49;\,\,\,x \ne 1\) thì \(A.B \le \frac{1}{2}\).

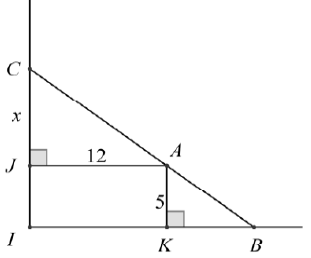
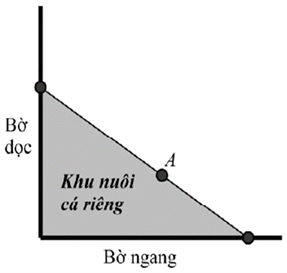
Đặt tên các điểm như hình vẽ. Đặt \(CJ = x,(x > 0).\)

Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên: \(\frac{{CJ}}{{AK}} = \frac{{JA}}{{KB}}\) hay \(\frac{x}{5} = \frac{{12}}{{KB}}\)

Suy ra \(KB = \frac{{60}}{x}.\)

Diện tích của khu nuôi cá là:\(S(x) = \frac{1}{2}\left( {x + 5} \right).\left( {\frac{{60}}{x} + 12} \right)\)

                        \(S(x) = \frac{1}{2}\left( {60 + 12x + \frac{{300}}{x} + 60} \right)\)

                            \(S(x) = 6x + \frac{{150}}{x} + 60\)

Áp dụng bất đẳng thức Cachy ta có: \(6x + \frac{{150}}{x} \ge 2\sqrt {6x.\frac{{150}}{x}}  = 60\)

                        Dấu bằng xảy ra khi: \(6x = \frac{{150}}{x}\)

\({x^2} = 25\)

\(x = 5\) (vì \(x > 0\))

                        Vậy \(S(x) = 6x + \frac{{150}}{x} + 60 \ge 60 + 60 = 120\).

                        Suy ra diện tích nhỏ nhất có thể giăng là \(120({m^2})\), đạt được khi \(x = 5\,m\).

Gọi giá tiền của bàn là và quạt điện theo giá niêm yết lần lượt là: \(x;\,y\) (đơn vị: nghìn đồng; điều kiện \(0 < x;\,y < 850\)).

Do tổng số tiền mua bàn là và quạt điện theo giá niêm yết là \[850\] nghìn đồng nên ta có phương trình:  \(x + y = 850\)   (1).

Bàn là giảm giá 20% nên số tiền cần trả cho bàn là là: \(x - \frac{{20}}{{100}}x = \frac{4}{5}x\) (nghìn đồng).

Quạt điện giảm giá 10% nên số tiền trả cho quạt điện là: \(y - \frac{{10}}{{100}}y = \frac{9}{{10}}y\) (nghìn đồng).

Tổng số tiền phải trả theo giá khuyến mại là \[740\] nghìn nên ta có phương trình:

\(\frac{4}{5}x + \frac{9}{{10}}y = 740\)     (2)

        Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y = 850\,\,\,\,\,\,\,\,\,\,}\\{\frac{4}{5}x + \frac{9}{{10}}y = 740}\end{array}} \right.\)

        Giải hệ ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 250}\\{y = 500}\end{array}} \right.\) (thỏa mãn điều kiện)

        Vậy giá tiền của bàn là là \[250\] nghìn đồng, của quạt điện là \[600\] nghìn đồng.