Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Quảng Ninh có đáp án
38 người thi tuần này 4.6 85 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) \(2\sqrt 9 - \sqrt {16} = 2 \cdot \sqrt {{3^2}} - \sqrt {{4^2}} = 2.3 - 4 = 6 - 4 = 2\)
b) Thay \({\rm{x}} = 1,{\rm{y}} = 2\) vào hàm số \(y = a{x^2}\) ta có:
\(2 = a{.1^2} \Leftrightarrow a = 2\).
Vậy \(a = 2\).
c) \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 7}\\{x - 2y = - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x + y = 7}\\{x = 2y - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2\left( {2y - 4} \right) + y = 7}\\{x = 2y - 4}\end{array}} \right.} \right.} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4y - 8 + y = 7}\\{x = 2y - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5y = 15}\\{x = 2y - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = 3}\\{x = 2y - 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 2}\\{y = 3}\end{array}} \right.} \right.} \right.} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {2;3} \right)\).
d) Với \(x \ge 0,x \ne 1,x \ne 9\) ta có:
\(P = \left( {\frac{1}{{\sqrt x - 3}} + \frac{2}{{\sqrt x + 3}}} \right):\frac{{\sqrt x - 1}}{{\sqrt x - 3}}\)
\(P = \frac{{\sqrt x + 3 + 2\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}:\frac{{\sqrt x - 1}}{{\sqrt x - 3}}\)
\(P = \frac{{\sqrt x + 3 + 2\sqrt x - 6}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} \cdot \frac{{\sqrt x - 3}}{{\sqrt x - 1}}\)
\(P = \frac{{3\sqrt x - 3}}{{\sqrt x + 3}} \cdot \frac{1}{{\sqrt x - 1}}\)
\(\; = \frac{{3\left( {\sqrt x - 1} \right)}}{{\sqrt x + 3}} \cdot \frac{1}{{\sqrt x - 1}}\)
\(P = \frac{3}{{\sqrt x + 3}}\)
Vậy với \(x \ge 0,x \ne 1,x \ne 9\) thì \(P = \frac{3}{{\sqrt x+ 3}}\).Lời giải
a) Khi \(m = 3\) phương trình trở thành: \({x^2} - 8x - 9 = 0\),
ta có: \({\rm{\Delta '}} = {( - 4)^2} - 1 \cdot \left( { - 9} \right) = 25 > 0\)
Suy ra phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{4 + \sqrt {25} }}{1} = 9;{x_2} = \frac{{4 - \sqrt {25} }}{1} = - 1\)
Vậy với \(m = 3\) phương trình có hai nghiệm phân biệt \({x_1} = 9;{x_2} = - 1\)
b) \(ac = 1.\left( { - 9} \right) < 0\) nên phương trình luôn có hai nghiệm phân biệt.
Phương trình có nghiệm \(x = 2\) nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{l}{2^2} - 2\left( {m + 1} \right)2 - 9 = 0 \Leftrightarrow 4 - 4m - 4 - 9 = 0\\ \Leftrightarrow - 4m - 9 = 0\\ \Leftrightarrow m = - \frac{9}{4}\end{array}\)
Vậy để phương trình có nghiệm \(x = 2\) thì \(m = - \frac{9}{4}\).
c) Xét phương trình \({x^2} - 2\left( {m + 1} \right)x - 9 = 0\) có \(a \cdot c = - 9 < 0\) nên phương trình luôn có 2 nghiệm trái dấu \({x_1},{x_2}\)
Áp dụng hệ thức viet ta có \({x_1} + {x_2} = 2\left( {m + 1} \right)\)
Mà \({x_1} < {x_2} \Rightarrow {x_1} < 0 < {x_2}\)
\(\left| {{x_1}} \right| - \left| {{x_2}} \right| = - 6\)
\( - {x_1} - {x_2} = - 6\)
\( \Leftrightarrow \)\( - \left( {{x_1} + {x_2}} \right) = - 6\)
\( \Leftrightarrow m + 1 = 3\)
\( \Leftrightarrow {x_1} + {x_2} = 6\)
Lời giải
Gọi vận tốc của xe thứ hai là \(x({\rm{\;km}}/{\rm{h}},x > 0)\).
Vì vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là \(10{\rm{\;km}}/{\rm{h}}\) nên vận tốc của xe thứ nhất là \(x + 10\) \(\left( {{\rm{km}}/{\rm{h}}} \right)\)
Thời gian xe thứ nhất đi từ \({\rm{A}}\) đến \({\rm{B}}\) là: \(\frac{{280}}{{x + 10}}\) (giờ)
Thời gian xe thứ hai đi từ \({\rm{A}}\) đến \({\rm{B}}\) là: \(\frac{{280}}{x}\) (giờ)
Vi xe thứ nhất đến \({\rm{B}}\) sớm hơn xe thứ hai 30 phút \( = \frac{1}{2}\) giờ nên ta có:
\(\frac{{280}}{x} - \frac{{280}}{{x + 10}} = \frac{1}{2}\)
\( \Leftrightarrow \frac{{560\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}} - \frac{{560x}}{{2x\left( {x + 10} \right)}} = \frac{{x\left( {x + 10} \right)}}{{2x\left( {x + 10} \right)}}\)
\( \Leftrightarrow 560\left( {x + 10} \right) - 560x = x\left( {x + 10} \right)\)
\( \Leftrightarrow 560x + 5600 - 560x = {x^2} + 10x\)
\( \Leftrightarrow {x^2} + 10x - 5600 = 0\)
\( \Leftrightarrow {x^2} - 70x + 80x - 5600 = 0\)
\[ \Leftrightarrow x\left( {x - 70} \right) + 80\left( {x - 70} \right) = 0\]
\( \Leftrightarrow \left( {x + 80} \right)\left( {x - 70} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 80 = 0}\\{x - 70 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 80{\rm{\;\;}}\left( {KTM} \right)}\\{x = 70{\rm{(TM)}}}\end{array}} \right)} \right.{\rm{\;}}\)
Vậy vận tốc xe thứ nhất là \(80{\rm{\;km}}/{\rm{h}}\), vận tốc xe thứ hai là \(70{\rm{\;km}}/{\rm{h}}\).Lời giải
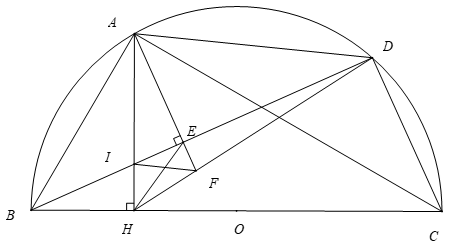
a) Do \[AH \bot BC\left( {gt} \right);AE \bot BD\left( {gt} \right) \Rightarrow \widehat {AHB} = \widehat {AEB} = 90^\circ \]
Mà \({\rm{E}},{\rm{H}}\) là hai đỉnh kề nhau, cùng nhìn \({\rm{AD}}\) dưới 2 góc bằng nhau nên \({\rm{A}},{\rm{E}},{\rm{H}},{\rm{B}}\) cùng thuộc một đường tròn.
Hay tứ giác \(ABHE\) nội tiếp (đpcm)
b) Ta có \(\widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BIH\) và \(\Delta BCD\) có:
\(\widehat {CBD}\) chung;
\[\widehat {BHI} = \widehat {BDC} = 90^\circ \]
\( \Rightarrow BI \cdot BD = BH \cdot BC\) (đpcm)
c) Do \(ABHE\) nội tiếp (cmt) nên \(\widehat {AHE} = \widehat {ABE}\) (hai góc nội tiếp cùng chắn cung \({\rm{AE}}\) )
Mà \(\widehat {ABE} = \widehat {ACD}\) (hai góc nội tiếp cùng chắn cung \({\rm{AD}}\) )
\( \Rightarrow \widehat {AHE} = \widehat {ACD}\).
Do \(ABHE\) nội tiếp (cmt) nên \(\widehat {HAE = }\widehat {HBE} = \widehat {CBD}\) (hai góc nội tiếp cùng chắn cung HE)
Lại có tứ giác \({\rm{ABCD}}\) nội tiếp \(\left( O \right) \Rightarrow \widehat {CBD} = \widehat {CAD}\) (hai góc nội tiếp cùng chắn cung \({\rm{CD}}\))
\( \Rightarrow \widehat {HAE} = \widehat {CAD}\)
Xét tam giác \({\rm{AHE}}\) và tam giác \({\rm{ACD}}\) có:
\[\widehat {AHE} = \widehat {ACD}\left( {{\rm{cmt}}} \right)\]
\[\widehat {HAE} = \widehat {CAD}\left( {{\rm{cmt}}} \right)\]
\[ \Rightarrow \Delta AEH \sim \Delta \Delta ADC\left( {g \cdot g} \right)\] \[\begin{array}{*{20}{r}}{}&{}\\{}&{}\\{}&\;\end{array}\]
d) Hai đường thẳng \(AE\) và \(DH\) cắt nhau tại \(F\). Chứng minh \(IF{\rm{//}}AD\).
Lời giải
Gọi cạnh hình lập phương bằng \(x\left( {{\rm{dm}}} \right)\). ĐK:
Gọi chiều cao bằng chiều rộng là ĐK: .
Chiều dài hình hộp chữ nhật bằng .
Hình lập phương có 12 cạnh có độ dài bằng .
Hình hộp chữ nhật có 8 cạnh có độ dài bằng và 4 cạnh có độ dài .
Người thợ cắt vừa đủ một cây sắt dài nên ta có:
\({\rm{x}} > 0\)
Thể tích khối lập phương là \({V_1} = {x^3}\).
Thể tích khối hộp chữ nhật là \({V_2} = y \cdot y \cdot 6y = 6{y^3}\).
Tổng thể tích hai hình là: \(V = {V_1} + {V_2} = {x^3} + 6{y^3} = {\left( {\frac{{25 - 8y}}{3}} \right)^3} + 6{y^3}\).
\(12x + 8y + 4.6y = 100 \Leftrightarrow 12x + 32y = 100 \Leftrightarrow 3x + 8y = 25 \Leftrightarrow x = \frac{{25 - 8y}}{3}\)
Ta có: \({x^3} + {3^3} + {3^3} \ge 3\sqrt[3]{{{x^3} \cdot {3^3} \cdot {3^3}}} = 27x\)
\(6\left( {{y^3} + {2^3} + {2^3}} \right) \ge 6 \cdot 3 \cdot \sqrt[3]{{{y^3} \cdot {2^3} \cdot {2^3}}} = 72y\)
Cộng vế theo vế hai bất đẳng thức ta được:
\({x^3} + 6{y^3} + 150 \ge 27x + 72y\)
\( \Leftrightarrow V + 150 \ge 9\left( {3x + 8y} \right)\)
\( \Leftrightarrow V + 150 \ge 9.25\)
\( \Leftrightarrow V + 150 \ge 225\)
\( \Leftrightarrow V \ge 75\)
Dấu "=" xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 2}\end{array}} \right.\).
Vậy tổng thể tích của hai hình thu được nhỏ nhất bằng \(75{\rm{d}}{{\rm{m}}^3}\) khi độ dài cạnh hình lập phương bằng \(3{\rm{dm}}\), độ dài chiều rộng và chiều cao hình hộp chữ nhật bằng \(2{\rm{dm}}\), chiều dài hình hộp chữ nhật bằng \(12{\rm{dm}}\).