Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Hòa Bình có đáp án
51 người thi tuần này 4.6 99 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1.\(\sqrt {x - 2} \) có nghĩa khi \(x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
2.\(\sqrt {36} + \sqrt 9 = 6 + 3 = 9\)
3a. Tìm được \(x = 2\)
b)Tìm đúng 2 nghiệm \({x_1} = 1;\,{x_2} = - 3\)
4a)Xác định được 2 điểm thuộc đồ thị.
Vẽ đúng đồ thị:
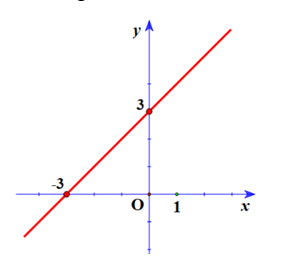
b)\[(d'):\,\,y = 2x + m - 1\] cắt đường thẳng \((d)\) tại một điểm trên trục tung
\( \Leftrightarrow m - 1 = 3 \Leftrightarrow m = 4\).
Lời giải
1)Tìm được nghiệm (x;y) = (1;1).
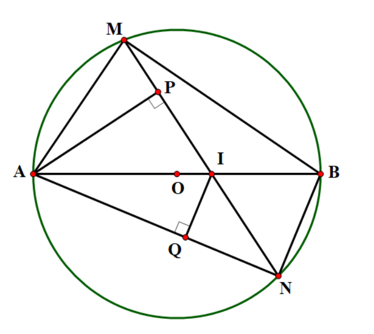
2)\(A{H^2} = HB.HC = 4.9 = 36 \Rightarrow AH = 6\,\,\,(cm)\)
Lời giải
1)\({\Delta ^'} = 16 - (m - 1) = 17 - m\)
Phương trình đã cho có hai nghiệm khi và chỉ khi \({\Delta ^'} \ge 0 \Leftrightarrow m \le 17\)
Áp dụng hệ thức Viet, ta có: \({x_1} + {x_2} = 8;{\rm{ }}{x_1}{x_2} = m - 1\)
\[P = {({x_1}{x_2})^2} - {x_1}^2 - {x_2}^2 + 2088 = {({x_1}{x_2})^2} - {({x_1} + {x_2})^2} + 2{x_1}{x_2} + 2088\]
\[ = {(m - 1)^2} - {8^2} + 2(m - 1) + 2088 = {m^2} + 2023 \ge 2023\].
Dấu "=" xảy ra khi và chỉ khi \(m = 0\,\,(TM)\)
2)Gọi số chiếc xe ban đầu của đội xe là \[x\] (\(x \in {N^*}\))
½ Số tấn xi măng mỗi xe phải chở theo dự định là: \(\frac{{120}}{x}\) (tấn).
Lập được phương trình: \(\frac{{120}}{x} = \frac{{125}}{{x + 5}} + 1\)
Giải phương trình tìm được \({x_1} = 20\,\,(TM);{\rm{ }}{x_2} = - 30\,\,(KTM)\)
KL: …
Lời giải
1.\(\begin{array}{l}2{x^2} + 3xy + {y^2} + 5x + 3y = 11\\ \Leftrightarrow (x + y + 2)(2x + y + 1) = 13\end{array}\)
Vì x, y nguyên nên (x;y) = (13; –14); (–12; 23); (–11; 8); (13; –28)
2.\(4{a^2} - 2ab + {b^2} = 4a + 2b \Leftrightarrow {a^2} - a.\frac{b}{2} + {\left( {\frac{b}{2}} \right)^2} = a + \frac{b}{2}\)
Đặt \(m = \frac{b}{2}\), ta có \({a^2} - am + {m^2} = a + m{\rm{ }}\left( 1 \right)\) và \(P = 253\left( {2a + b} \right) = 506\left( {a + \frac{b}{2}} \right) = 506\left( {a + m} \right)\)
\[\left( 1 \right) \Leftrightarrow {\left( {a + m} \right)^2} - 3{\rm{am}} = a + m \Leftrightarrow {\left( {a + m} \right)^2} = \left( {a + m} \right) + 3{\rm{am}}\].
Chứng minh được \({\left( {a + m} \right)^2} \ge 4{\rm{am}} \Leftrightarrow am \le \frac{{{{\left( {a + m} \right)}^2}}}{4}\).
Suy ra \({\left( {a + m} \right)^2} = \left( {a + m} \right) + 3{\rm{am}} \le \left( {a + m} \right) + \frac{3}{4}{\left( {a + m} \right)^2} \Leftrightarrow \frac{1}{4}{\left( {a + m} \right)^2} \le a + m\)
\[ \Leftrightarrow \left( {a + m} \right)\left[ {\left( {a + m} \right) - 4} \right] \le 0 \Leftrightarrow 0 \le a + m \le 4\].
Do đó \(0 \le P \le 4.506 \Leftrightarrow 0 \le P \le 2024\).
Vậy \(\,\max P = 2024 \Leftrightarrow a = m = 2 \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.\).