Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 33
56 người thi tuần này 4.6 147 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
a)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,4;8,6} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{5.100}}{{100}}\% = 5\% ;.\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,6;8,8} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{12.100}}{{100}}\% = 12\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,8;9,0} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{25.100}}{{100}}\% = 25\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,0;9,2} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{44.100}}{{100}}\% = 44\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,2;9,4} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{14.100}}{{100}}\% = 14\% ;\)
Vì vậy, bảng tần ghép nhóm của mẫu số liệu đã cho được nêu trong bảng dưới đây.
|
Chiều cao (\[m\]) |
\(\left[ {8,4;8,6} \right)\) |
\(\left[ {8,6;8,8} \right)\) |
\(\left[ {8,8;9,0} \right)\) |
|
\(\left[ {9,0;9,2} \right)\) |
\(\left[ {9,2;9,4} \right)\) |
Tổng |
|
Tần số tương đối (\(\% \)) |
\(5\) |
\(12\) |
\(25\) |
|
\(44\) |
\(14\) |
\(100\) |
b) Biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng
thống kê thu được ở câu a
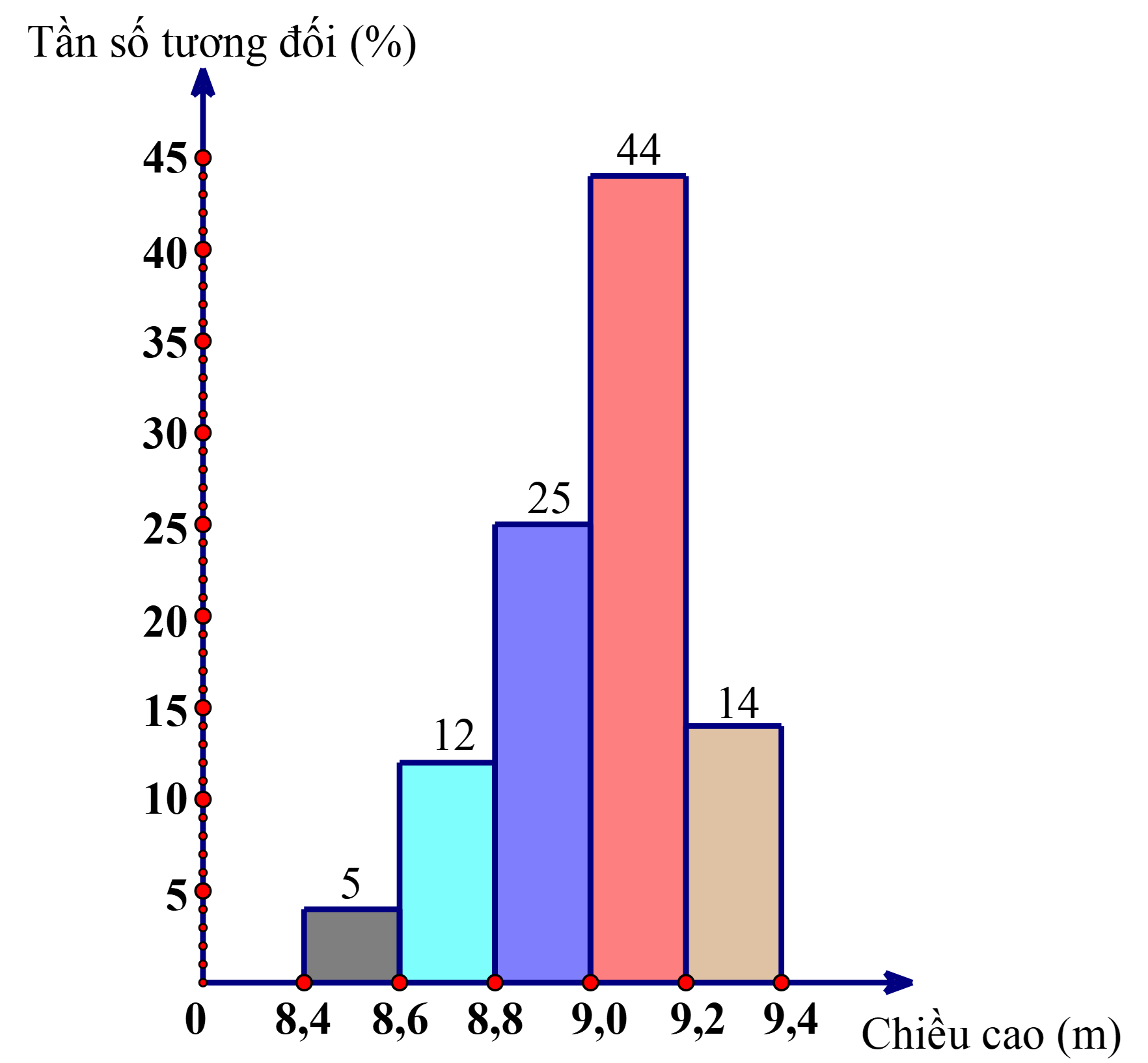
Lời giải
- Có \(20\) kết quả có thể xảy ra của phép thử “Số xuất hiện trên thẻ được lấy ra” là: \(1;\;2;\;3;\;...\;;19;\;20.\)
a) Những kết quả thuận lợi của biến cố A: “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là \(2\)” là: \(2;\;12.\) Có \(2\) kết quả thuận lợi
Vậy xác suất của biến cố A là: \(\frac{2}{{20}} = \frac{1}{{10}}\)
b) Những kết quả thuận lợi của biến cố B: “Số xuất hiện trên thẻ được rút ra là số nguyên tố” là: \(2;\;3;5;7;11;13;17;19.\) Có \(8\) kết quả thuận lợi
Vậy xác suất của biến cố B là: \(\frac{8}{{20}} = \frac{2}{5}\)
b) Những kết quả thuận lợi của biến cố C: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng \[4\]” là: \(14.\) Có \(1\) kết quả thuận lợi
Vậy xác suất của biến cố C là: \(\frac{1}{{20}}\)
Lời giải
ĐK: \(x \ge 0;x \ne 9\)
1) Với \(x = 49\)(TMĐK) nên \(\sqrt x = 7\) Thay vào \(A\) ta được:
\(A = \frac{{49 + 7}}{{7 - 3}}\)
\(A = 14\)
2)
\(B = \frac{{\sqrt x }}{{\sqrt x - 3}} + \frac{{6\sqrt x }}{{9 - x}} - \frac{3}{{\sqrt x + 3}}\)
\(B = \frac{{\sqrt x }}{{\sqrt x - 3}} - \frac{{6\sqrt x }}{{x - 9}} - \frac{3}{{\sqrt x + 3}}\)
\(B = \frac{{\sqrt x }}{{\sqrt x - 3}} - \frac{{6\sqrt x }}{{(\sqrt x - 3)(\sqrt x + 3)}} - \frac{3}{{\sqrt x + 3}}\)
\(B = \frac{{\sqrt x (\sqrt x + 3) - 6\sqrt x - 3(\sqrt x - 3)}}{{(\sqrt x - 3)(\sqrt x + 3)}}\)
\(B = \frac{{x + 3\sqrt x - 6\sqrt x - 3\sqrt x + 9}}{{(\sqrt x - 3)(\sqrt x + 3)}}\)
\(B = \frac{{x - 6\sqrt x + 9}}{{(\sqrt x - 3)(\sqrt x + 3)}}\)
\(B = \frac{{{{(\sqrt x - 3)}^2}}}{{(\sqrt x - 3)(\sqrt x + 3)}}\)
\(B = \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\)
3) Ta có \(M = A.B = \frac{{x + 7}}{{\sqrt x - 3}}.\frac{{\sqrt x - 3}}{{\sqrt x + 3}}\)
\(M = \frac{{x + 7}}{{\sqrt x + 3}}\)
\(M = \frac{{x - 9 + 16}}{{\sqrt x + 3}}\)
\(M = \sqrt x - 3 + \frac{{16}}{{\sqrt x + 3}}\)
\(M = \sqrt x + 3 + \frac{{16}}{{\sqrt x + 3}} - 6\)
Với a,b \( \ge 0\) ta có \({\left( {\sqrt a - \sqrt b } \right)^2} \ge 0\) nên \(a + b \ge 2\sqrt {ab} \). Dấu bằng xảy ra khi a = b
Áp dụng bất đẳng thức trên ta có \(x \ge 0\)nên \(\sqrt x + 3 > 0,\frac{{16}}{{\sqrt x + 3}} > 0\)
Do đó \(\sqrt x + 3 + \frac{{16}}{{\sqrt x + 3}} \ge 2\sqrt {(\sqrt x + 3).\frac{{16}}{{\sqrt x + 3}}} = 8\)
\(\sqrt x + 3 + \frac{{16}}{{\sqrt x + 3}} - 6 \ge 8 - 6 = 2\)
Nên M\( \ge 2\) Suy ra Min M= 2 khi
\(\sqrt x + 3 = \frac{{16}}{{\sqrt x + 3}}\)
\({(\sqrt x + 3)^2} = 16\)
\(\sqrt x + 3 = 4\)
\(\sqrt x = 1\)
Lời giải
Gọi chiều rộng của hình chữ nhật đáy bể là \(x\)(m) (\(x > 0\))
Suy ra chiều dài của hình chữ nhật là \(4x\)(m).
Gọi chiều cao của bể là \(y\) (m, \(y > 0\)).
Thể tích của bể là \[V = 4x.x.y = 400\] suy ra \[{x^2}.y = 100\] suy ra\[y = \frac{{100}}{{{x^2}}}\].
Diện tích xây dựng của bể là \[S = 4{x^2} + 2\left( {x + 4x} \right)y\]\[ = 4{x^2} + 10xy\]\[ = 4{x^2} + 10.\frac{{100}}{{{x^2}}}.x\]\[ = 4{x^2} + \frac{{1000}}{x}\]
Áp dụng bất đẳng thức AM – GM cho 2 số không âm (với hai số không âm \(x,y\) ta có \({\left( {\sqrt x - \sqrt y } \right)^2} \ge 0\)nên \(x + y - 2\sqrt {xy} \ge 0\) suy ra \(x + y \ge 2\sqrt {xy} \), dấu bằng xảy ra khi \[x = y\]):
Ta có \[S = 4{x^2} + \frac{{1000}}{x}\]\[ = \left( {4{x^2} + 100} \right) + \frac{{1000}}{x} - 100\]\[ \ge 2\sqrt {4{x^2}.100} + \frac{{1000}}{x} - 100\]\[ = 40x + \frac{{1000}}{x} - 100\].
Và \[S \ge 40x + \frac{{1000}}{x} - 100\]\[ \ge 2\sqrt {40x.\frac{{1000}}{x}} - 100\]\[ = 400 - 100 = 300\].
Khi đó \({S_{\min }} = 300\).
Dấu “\( = \)” xảy ra khi \[\left\{ {\begin{array}{*{20}{c}}{4{x^2} = 100}\\{40x = \frac{{1000}}{x}}\end{array}} \right.\] suy ra \[x = 5\]
Vậy chi phí thấp nhất thuê nhân công là \[300.500\,000 = 150\,000\,000\] đồng \( = 150\)triệu đồng
Đoạn văn 2
Lời giải
Gọi số áo tổ một may được trong một ngày là \[x\] (áo), (\(x \in {\mathbb{N}^*};\;x > 10\)).
Gọi số áo tổ hai may được trong một ngày là \[y\] (áo), (\(y \in {\mathbb{N}^*}\)).
Vì tổ thứ nhất may trong \[3\] ngày, tổ thứ hai may trong \[5\] ngày thì cả hai tổ may được \[1310\] chiếc áo nên ta có phương trình : \(3x + 5y = 1310\) (1).
Vì trong mỗi ngày tổ thứ nhất may được nhiều hơn tổ thứ hai \[10\] chiếc áo nên ta có phương trình: \(x - y = 10\) hay \(x = y + 10\).
Thay \(x = y + 10\) vào phương trình (1) ta được:
\(3\left( {y + 10} \right) + 5y = 1310\)
\(3y + 30 + 5y = 1310\)
\(8y = 1280\)
\(y = 160\) (tm).
Suy ra \(x = 160 + 10 = 170\) (tm).
Mỗi ngày tổ một may được \(170\) áo, tổ hai may được \(160\) áo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.