(1,5 điểm)
Kết quả đo chiều cao của \[100\] cây keo \[3\] năm tuổi tại một nông trường được cho ở bảng sau:
Chiều cao (\[m\])
\(\left[ {8,4;8,6} \right)\)
\(\left[ {8,6;8,8} \right)\)
\(\left[ {8,8;9,0} \right)\)
\(\left[ {9,0;9,2} \right)\)
\(\left[ {9,2;9,4} \right)\)
Tổng
Số cây
\(5\)
\(12\)
\(25\)
\(44\)
\(14\)
\[100\]
a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê thu được ở câu a.
Kết quả đo chiều cao của \[100\] cây keo \[3\] năm tuổi tại một nông trường được cho ở bảng sau:
|
Chiều cao (\[m\]) |
\(\left[ {8,4;8,6} \right)\) |
\(\left[ {8,6;8,8} \right)\) |
\(\left[ {8,8;9,0} \right)\) |
\(\left[ {9,0;9,2} \right)\) |
\(\left[ {9,2;9,4} \right)\) |
Tổng |
|
Số cây |
\(5\) |
\(12\) |
\(25\) |
\(44\) |
\(14\) |
\[100\] |
a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê thu được ở câu a.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 33 !!
Quảng cáo
Trả lời:
a)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,4;8,6} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{5.100}}{{100}}\% = 5\% ;.\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,6;8,8} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{12.100}}{{100}}\% = 12\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,8;9,0} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{25.100}}{{100}}\% = 25\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,0;9,2} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{44.100}}{{100}}\% = 44\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,2;9,4} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{14.100}}{{100}}\% = 14\% ;\)
Vì vậy, bảng tần ghép nhóm của mẫu số liệu đã cho được nêu trong bảng dưới đây.
|
Chiều cao (\[m\]) |
\(\left[ {8,4;8,6} \right)\) |
\(\left[ {8,6;8,8} \right)\) |
\(\left[ {8,8;9,0} \right)\) |
|
\(\left[ {9,0;9,2} \right)\) |
\(\left[ {9,2;9,4} \right)\) |
Tổng |
|
Tần số tương đối (\(\% \)) |
\(5\) |
\(12\) |
\(25\) |
|
\(44\) |
\(14\) |
\(100\) |
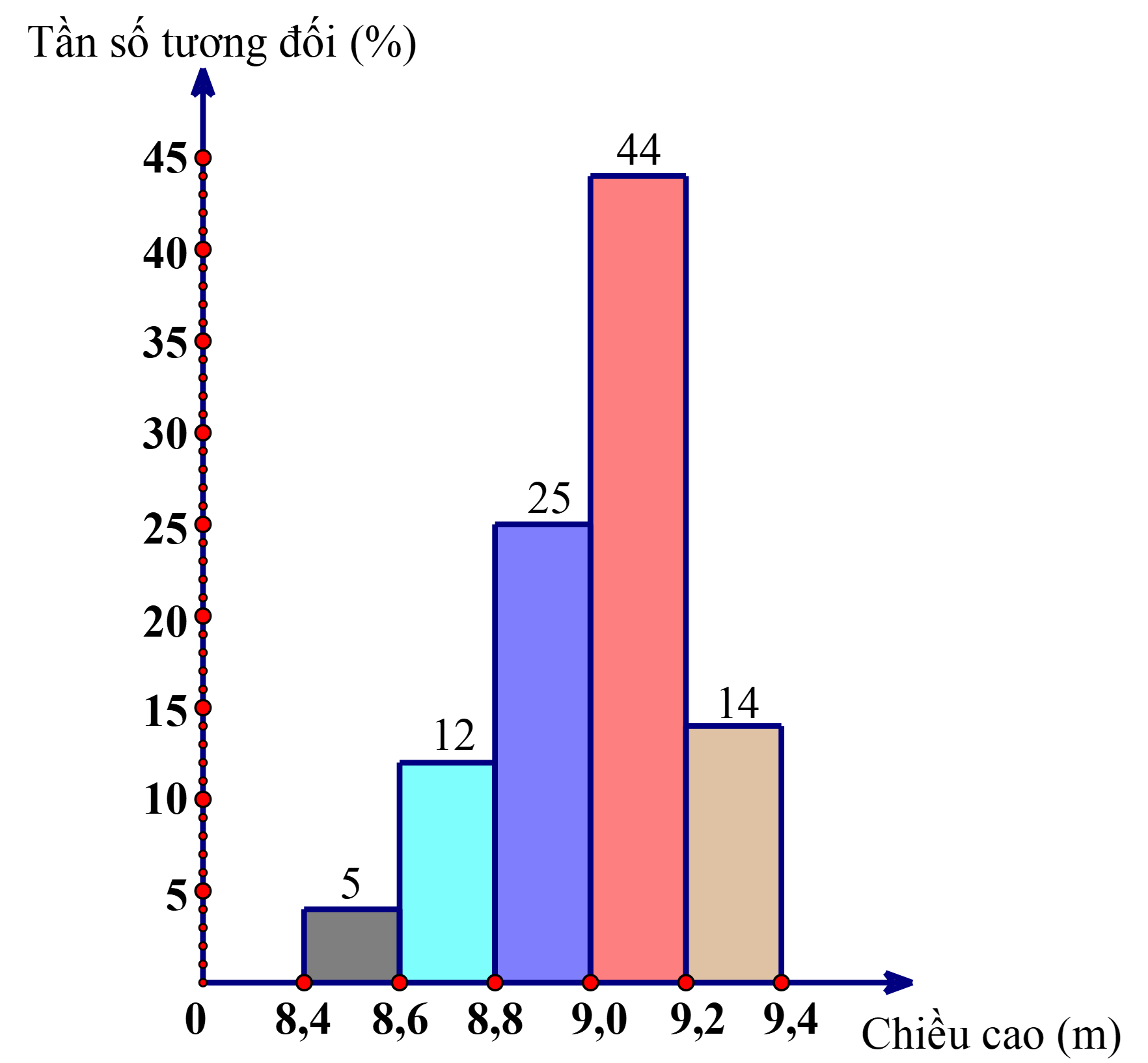
b) Biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng
thống kê thu được ở câu a
Câu hỏi cùng đoạn
Câu 2:
Một hộp có \[20\] thể cùng loại, mỗi thẻ được ghi một trong các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }} \ldots {\rm{ }};{\rm{ }}20\], hai thẻ khác nhau thì ghi số khác nhau .Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) Biến cố A: “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là \[2\]”.
b) Biến cố B: “Số xuất hiện trên thẻ được rút ra là số nguyên tố”.
c) Biến cố C: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng \[4\]”.
Một hộp có \[20\] thể cùng loại, mỗi thẻ được ghi một trong các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }} \ldots {\rm{ }};{\rm{ }}20\], hai thẻ khác nhau thì ghi số khác nhau .Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) Biến cố A: “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là \[2\]”.
b) Biến cố B: “Số xuất hiện trên thẻ được rút ra là số nguyên tố”.
c) Biến cố C: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng \[4\]”.
- Có \(20\) kết quả có thể xảy ra của phép thử “Số xuất hiện trên thẻ được lấy ra” là: \(1;\;2;\;3;\;...\;;19;\;20.\)
a) Những kết quả thuận lợi của biến cố A: “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là \(2\)” là: \(2;\;12.\) Có \(2\) kết quả thuận lợi
Vậy xác suất của biến cố A là: \(\frac{2}{{20}} = \frac{1}{{10}}\)
b) Những kết quả thuận lợi của biến cố B: “Số xuất hiện trên thẻ được rút ra là số nguyên tố” là: \(2;\;3;5;7;11;13;17;19.\) Có \(8\) kết quả thuận lợi
Vậy xác suất của biến cố B là: \(\frac{8}{{20}} = \frac{2}{5}\)
b) Những kết quả thuận lợi của biến cố C: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng \[4\]” là: \(14.\) Có \(1\) kết quả thuận lợi
Vậy xác suất của biến cố C là: \(\frac{1}{{20}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chiều rộng của hình chữ nhật đáy bể là \(x\)(m) (\(x > 0\))
Suy ra chiều dài của hình chữ nhật là \(4x\)(m).
Gọi chiều cao của bể là \(y\) (m, \(y > 0\)).
Thể tích của bể là \[V = 4x.x.y = 400\] suy ra \[{x^2}.y = 100\] suy ra\[y = \frac{{100}}{{{x^2}}}\].
Diện tích xây dựng của bể là \[S = 4{x^2} + 2\left( {x + 4x} \right)y\]\[ = 4{x^2} + 10xy\]\[ = 4{x^2} + 10.\frac{{100}}{{{x^2}}}.x\]\[ = 4{x^2} + \frac{{1000}}{x}\]
Áp dụng bất đẳng thức AM – GM cho 2 số không âm (với hai số không âm \(x,y\) ta có \({\left( {\sqrt x - \sqrt y } \right)^2} \ge 0\)nên \(x + y - 2\sqrt {xy} \ge 0\) suy ra \(x + y \ge 2\sqrt {xy} \), dấu bằng xảy ra khi \[x = y\]):
Ta có \[S = 4{x^2} + \frac{{1000}}{x}\]\[ = \left( {4{x^2} + 100} \right) + \frac{{1000}}{x} - 100\]\[ \ge 2\sqrt {4{x^2}.100} + \frac{{1000}}{x} - 100\]\[ = 40x + \frac{{1000}}{x} - 100\].
Và \[S \ge 40x + \frac{{1000}}{x} - 100\]\[ \ge 2\sqrt {40x.\frac{{1000}}{x}} - 100\]\[ = 400 - 100 = 300\].
Khi đó \({S_{\min }} = 300\).
Dấu “\( = \)” xảy ra khi \[\left\{ {\begin{array}{*{20}{c}}{4{x^2} = 100}\\{40x = \frac{{1000}}{x}}\end{array}} \right.\] suy ra \[x = 5\]
Vậy chi phí thấp nhất thuê nhân công là \[300.500\,000 = 150\,000\,000\] đồng \( = 150\)triệu đồng
Lời giải
a) Chiều cao của hộp hình trụ: \(3.6,2 = 18,6{\rm{ }}\left( {cm} \right)\)
Bán kính của hình tròn đáy hình trụ: \(6,2:2 = 3,1{\rm{ }}\left( {cm} \right)\)
Thể tích của hộp hình trụ là: \(V = \pi {R^2}h \approx {3,14.3,1^2}.18,6\)\( \approx 561,3{\rm{ }}\left( {c{m^3}} \right)\)
b) Thể tích của 3 quả bóng tenis là: \(V = 3.\frac{4}{3}\pi {R^3}\)\( \approx 3.\frac{4}{3}{.3,14.3,1^3}\)\( \approx 93,5{\rm{ }}\left( {c{m^3}} \right)\)
Thể tích phần không gian còn trống bên trong là: \(561,3 - 93,5 = 467,8{\rm{ }}\left( {c{m^3}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.