Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Bình Thuận có đáp án
48 người thi tuần này 4.6 108 lượt thi 7 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) \({x^2} + 2x - 3 = 0\)
Ta có: \(\Delta = {2^2} - 4.1.\left( { - 3} \right) = 16 > 0\) \( \Rightarrow \sqrt \Delta = \sqrt {16} = 4\)
Do đó phương trình có hai nghiệm phân biệt
\({x_1} = \frac{{ - 2 - 4}}{{2.1}} = - 3\)
\({x_2} = \frac{{ - 2 + 4}}{{2.1}} = 1\)
Vậy tập nghiệm phương trình \(S = \left\{ { - 3;{\rm{ 1}}} \right\}\)
Cách khác:
\({x^2} + 2x - 3 = 0\)
Có \(a + b + c = 1 + 2 + \left( { - 3} \right) = 0\)
Nên \({x_1} = 1\)
\({x_2} = \frac{c}{a} = \frac{{ - 3}}{1} = - 3\)
Vậy tập nghiệm phương trình \(S = \left\{ { - 3;{\rm{ 1}}} \right\}\)
b) \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array}} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}4y = 8\\x + y = 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x + 2 = 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\)
Vậy tập nghiệm hệ phương trình \(S = \left\{ {\left( {1;{\rm{ }}2} \right)} \right\}\)
Lời giải
a) \(A = \left( {\sqrt {27} - \sqrt {12} + \sqrt {48} } \right)\sqrt 3 \)
\[A = \left( {\sqrt {9.3} - \sqrt {4.3} + \sqrt {16.3} } \right)\sqrt 3 \]
\[A = \left( {3\sqrt 3 - 2\sqrt 3 + 4\sqrt 3 } \right)\sqrt 3 \]
\[A = 5\sqrt 3 .\sqrt 3 \]
\(A = 15\)
b) \(B = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\) với \(0 < x\) và \(x \ne 1\).
\(B = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{{\sqrt x + 1}}{{3\sqrt x }}\)
\(B = \left( {\frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right).\frac{{3\sqrt x }}{{\sqrt x + 1}}\)
\(B = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{3\sqrt x }}{{\sqrt x + 1}}\)
\(B = 3\)
Lời giải
a) Vẽ đồ thị \((P)\)trên mặt phẳng tọa độ \[Oxy\].
Bảng giá trị:
Đồ thị hàm số \(y = {x^2}\) là một Parabol \((P)\) đi qua các điểm \(\left( { - 2;{\rm{ 4}}} \right)\), \(\left( { - 1;{\rm{ 1}}} \right)\); \(\left( {0;{\rm{ 0}}} \right)\); \(\left( {1;{\rm{ 1}}} \right)\), \(\left( {2;{\rm{ 4}}} \right)\)
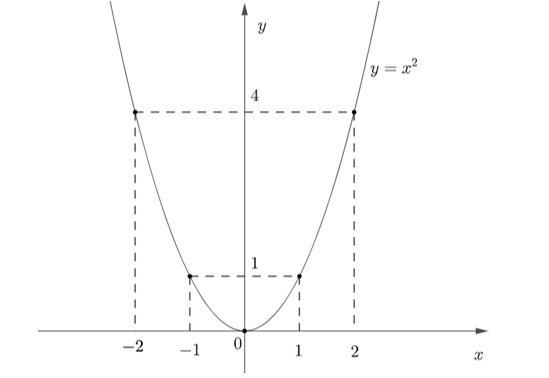
b) Tìm giá trị nguyên của tham số \(m\) để đường thẳng \((d):y = 2mx - {m^2} + 1\) cắt \((P)\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\) thỏa mãn \({x_1} < 2024 < {x_2}\).
Hoành độ giao điểm của \((d)\) và \((P)\) là nghiệm phương trình:
\({x^2} = 2mx - {m^2} + 1\)
\( \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\) \(\left( 1 \right)\)
Đường thẳng \((d)\) cắt \((P)\) tại 2 điểm phân biệt khi và chỉ khi phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt
\( \Leftrightarrow \Delta ' > 0\)
\( \Leftrightarrow {\left( { - m} \right)^2} - 1.\left( {{m^2} - 1} \right) > 0\)
\( \Leftrightarrow {m^2} - {m^2} + 1 > 0\)
\( \Leftrightarrow 1 > 0\) (Hiển nhiên)
Phương trình \(\left( 1 \right)\) luôn có 2 nghiệm phân biệt \({x_1},{x_2}\) hay đường thẳng \((d)\) luôn cắt \((P)\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\) với mọi giá trị \(m\).
\({x_1} = \frac{{m - \sqrt 1 }}{1} = m - 1\)
\({x_1} = \frac{{m + \sqrt 1 }}{1} = m + 1\)
Ta có: \({x_1} < 2024 < {x_2}\)
\( \Leftrightarrow m - 1 < 2024 < m + 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}m - 1 < 2024\\m + 1 > 2024\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 2025\\m > 2023\end{array} \right.\)
\( \Leftrightarrow m = 2024\) (Vì cần tìm \(m\) có giá trị nguyên)
Vậy \(m = 2024\) thì \((d)\) cắt \((P)\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1},{x_2}\) thỏa mãn \({x_1} < 2024 < {x_2}\).
Lời giải
Gọi số xe nhỏ (chiếc) công ty đã thuê là \(x\), \(\left( {x \in \mathbb{N},{\rm{ }}x > 2} \right)\).
Do đó số xe lớn (chiếc) công ty dự định thuê là \(x - 2\).
Số xe lớn và nhỏ đều chở vừa hết 210 người nên:
Số người trên xe nhỏ là: \(\frac{{210}}{x}\) (người)
Số người trên xe lớn là: \(\frac{{210}}{{x - 2}}\) (người)
Theo đề mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người, nên ta có phương trình:
\(\frac{{210}}{{x - 2}} - \frac{{210}}{x} = 12\)
\( \Leftrightarrow 210x - 210\left( {x - 2} \right) = 12x\left( {x - 2} \right)\)
\( \Leftrightarrow 210x - 210x + 420 = 12{x^2} - 24x\)
\( \Leftrightarrow 12{x^2} - 24x - 420 = 0\)
\( \Leftrightarrow 12\left( {x - 7} \right)\left( {x + 5} \right) = 0\)
\[ \Leftrightarrow \left[ \begin{array}{l}x - 7 = 0\\x + 5 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 7{\rm{ }}}&{\left( {{\rm{Nha\"a n}}} \right)}\\{x = - 5}&{\left( {{\rm{Loa\"i i}}} \right)}\end{array}} \right.\]
Vậy công ty đã thuê 7 chiếc xe nhỏ.
Lời giải
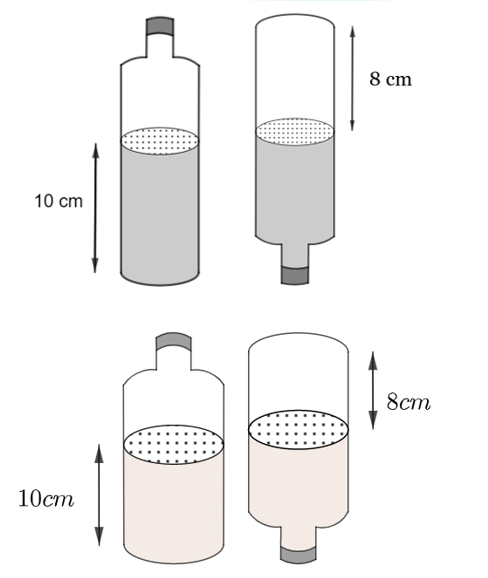
Gọi \(R\) (cm) là bán kính đáy chai. \[\left( {R > 0} \right)\]
Thể tích nước trong chai (hình trụ có chiều cao 10 cm) là:
\[{V_1} = \pi {R^2}.{h_1} = 10\pi {R^2}\] \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích không chứa nước trong chai khi lật ngược chai (hình trụ có chiều cao 8 cm) là:
\[{V_2} = \pi {R^2}.{h_2} = 8\pi {R^2}\] \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích của chai (\[450\pi \] \({\rm{c}}{{\rm{m}}^3}\)) là tổng thể tích của nước và phần không chứa nước trong chai khi lật ngược chai lại, nên ta có:\[{V_1} + {V_2} = 450\pi \]
\( \Leftrightarrow 10\pi {R^2} + 8\pi {R^2} = 450\pi \)
\( \Leftrightarrow 18\pi {R^2} = 450\pi \)
\( \Leftrightarrow {R^2} = 25\)
\( \Rightarrow R = 5\) (Do \[R > 0\])
Vậy bán kính của đáy chai là 5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.