Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao 10 cm, khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao 8 cm (như hình vẽ bên. Biết thể tích của chai là \(450\pi \)\({\rm{c}}{{\rm{m}}^{\rm{3}}}\). Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).
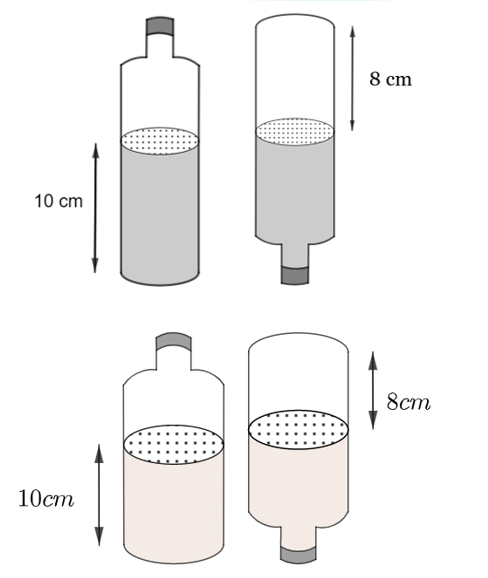
Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao 10 cm, khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao 8 cm (như hình vẽ bên. Biết thể tích của chai là \(450\pi \)\({\rm{c}}{{\rm{m}}^{\rm{3}}}\). Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).

Quảng cáo
Trả lời:
Gọi \(R\) (cm) là bán kính đáy chai. \[\left( {R > 0} \right)\]
Thể tích nước trong chai (hình trụ có chiều cao 10 cm) là:
\[{V_1} = \pi {R^2}.{h_1} = 10\pi {R^2}\] \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích không chứa nước trong chai khi lật ngược chai (hình trụ có chiều cao 8 cm) là:
\[{V_2} = \pi {R^2}.{h_2} = 8\pi {R^2}\] \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích của chai (\[450\pi \] \({\rm{c}}{{\rm{m}}^3}\)) là tổng thể tích của nước và phần không chứa nước trong chai khi lật ngược chai lại, nên ta có:\[{V_1} + {V_2} = 450\pi \]
\( \Leftrightarrow 10\pi {R^2} + 8\pi {R^2} = 450\pi \)
\( \Leftrightarrow 18\pi {R^2} = 450\pi \)
\( \Leftrightarrow {R^2} = 25\)
\( \Rightarrow R = 5\) (Do \[R > 0\])
Vậy bán kính của đáy chai là 5 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
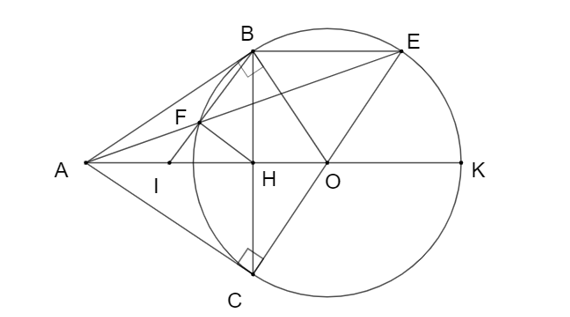
a) Xét tứ giác \(ABOC\) có:
\(\widehat {ABO} = \widehat {ACO} = 90^\circ \) (\(AB\), \(AC\) lần lượt là tiếp tuyến tại \(B\), \(C\) của \(\left( O \right)\))
\( \Rightarrow \widehat {ABO} + \widehat {ACO} = 180^\circ \)
Vậy tứ giác \(ABOC\) nội tiếp (Hai góc đối bù nhau)
b) Xét \(\Delta ABF\) và \(\Delta AEB\) có:
\(\widehat {BAF}\) là góc chung
\(\widehat {ABF} = \widehat {AEB}\)
Do đó \(\Delta ABF \sim \Delta AEB\) (g – g)
\[ \Rightarrow \frac{{AB}}{{AF}} = \frac{{AE}}{{AB}}\] (tính chất hai tam giác đồng dạng)
\( \Rightarrow A{B^2} = AE.AF\)
c) Xét \(\left( O \right)\) có \(AB\), \(AC\) lần lượt là tiếp tuyến tại \(B\), \(C\) của \(\left( O \right)\), \(OA \cap BC = H\)
\( \Rightarrow OA \bot BC\) tại \(H\)
Xét \(\Delta ABO\) vuông tại \(B\), đường cao \(BH\), ta có:
\(A{B^2} = AH.AO\)
Do đó \(AE.AF = AH.AO\) \(\left( { = A{B^2}} \right)\)
\( \Rightarrow \frac{{AE}}{{AH}} = \frac{{AO}}{{AF}}\)
Xét \(\Delta AEO\) và \(\Delta AHF\), ta có:
\(\widehat {HAF}\) là góc chung
\(\frac{{AE}}{{AH}} = \frac{{AO}}{{AF}}\)
Do đó \(\Delta AEO \sim \Delta AHF\) (c – g – c)
\( \Rightarrow \widehat {AEO} = \widehat {AHF}\) (Hai góc tương ứng)
Mà \(\widehat {AHF} + \widehat {FHO} = 180^\circ \) (hai góc kề bù)
nên \(\widehat {AEO} + \widehat {FHO} = 180^\circ \) hay \(\widehat {FEO} + \widehat {FHO} = 180^\circ \)
Suy ra tứ giác \(OHFE\) nội tiếp (Hai góc đối bù nhau)
\( \Rightarrow \widehat {HFE} + \widehat {HOE} = 180^\circ \) (Tính chất tứ giác nội tiếp)
Kéo dài \(AO\) cắt \(\left( O \right)\) tại \(K\) (\(O\) nằm giữa \(A\) và \(K\)ta có:\(\widehat {KOE} + \widehat {HOE} = 180^\circ \)
\( \Rightarrow \widehat {KOE} = \widehat {HFE}\) (Cùng bù \(\widehat {HOE}\))
Xét \(\left( O \right)\), ta có:
\(\widehat {EBC} = 90^\circ \) (Góc nội tiếp chắn nửa đường tròn)
\[ \Rightarrow EB \bot BC\]
Mặt khác, ta có:\( \Rightarrow OA \bot BC\) tại \(H\) (cmt)\( \Rightarrow AK \bot BC\)
Do đó: \(EB{\rm{ // }}AK\) (cùng vuông góc với \(BC\)) \( \Rightarrow \widehat {KOE} = \widehat {OEB}\) (Hai góc so le trong)
\( \Rightarrow \widehat {KOE} = \widehat {CEB}\)
Suy ra\(\widehat {HFE} = \widehat {CEB}{\rm{ }}\left( { = \widehat {KOE}} \right)\)
Xét \(\left( O \right)\), ta có: \(\widehat {BFE} = \widehat {BCE}\)
Trong \(\Delta EBC\) vuông tại \(B\), ta có: \(\widehat {BEC} + \widehat {BCE} = 90^\circ \)
Ta có:
\(\widehat {BFH} = \widehat {BFE} + \w\(HF\)idehat {HFE} = \widehat {BCE} + \widehat {BEC} = 90^\circ \)\( \Rightarrow HF \bot BI\) tại \(F\)
Xét \(\Delta BHI\) vuông tại \(H\), đường cao , ta có:
\(I{H^2} = IF.IB\) \(\left( 1 \right)\)
Xét \[\Delta IAF\] và \[\Delta IBA\], ta có:
\(\widehat {AIF}\) là góc chung
\(\widehat {IBA} = \widehat {IAF}\) (\(\widehat {IBA} = \widehat {BEF}\) cùng chắn cung \(BF\) của \(\left( O \right)\), \(\widehat {BEF} = \widehat {IAF}\)là hai góc so le trong của \(EB{\rm{ // }}AK\))
Vậy \[\Delta IAF \sim \Delta IBA\] (g – g)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{IF}}{{IA}}\)
\( \Rightarrow I{A^2} = IF.IB\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow I{H^2} = I{A^2}\)
\( \Rightarrow IH = IA\) hay \(I\) là trung điểm \(AH\)
Lời giải
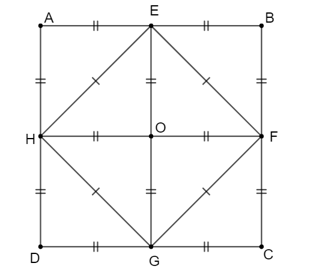
Nhận xét:
Xét hình vuông \(ABCD\), gọi \(E,{\rm{ }}F,{\rm{ }}G,{\rm{ }}H\) lần lượt là trung điểm \(AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA\).
Khi đó hình vuông \[EFGH\] có các đỉnh là trung điểm của các cạnh hình vuông \(ABCD\)
Dễ dàng nhận thấy\(\Delta AEH = \Delta BEH = \Delta CGF = \Delta DGH = \Delta OEH = \Delta OEF = \Delta OGF = \Delta OHG\) (c – c – c) (hoặc trường hợp hai cạnh góc vuông)
Do đó \({S_{ABCD}} = 8.{S_{\Delta OHG}}\), \({S_{EFGH}} = 4.{S_{\Delta OHG}}\)
\( \Rightarrow {S_{ABCD}} = 2{S_{EFGH}}\)
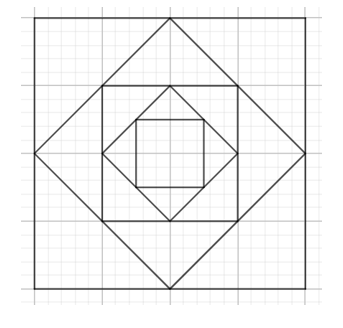
Quay lại bài toán, gọi \({S_1};{\rm{ }}{S_2};{\rm{ }}{S_3};{\rm{ }}{S_4};{\rm{ }}{S_5};{\rm{ }}{S_6};{\rm{ }}{S_7}\) lần lượt là điện tích của các hình vuông \(1;{\rm{ 2}};{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7\)
Theo nhận xét, ta có: Diện tích hình vuông bất kì bằng hai lần diện tích hình vuông có các đỉnh là trung điểm của các cạnh hình vuông đã cho.
Do đó ta có:
\({S_5} = 2{S_6} = 2.2{S_7} = 4{S_7} = 4.32 = 128\) \(\left( {c{m^2}} \right)\)
Vậy diện tích hình vuông thứ 5 là 128 \(c{m^2}\)
Cách khác:
Nhận xét:
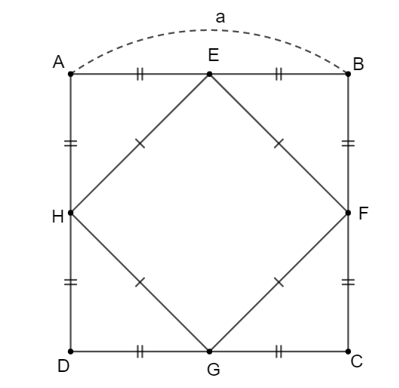
Xét hình vuông \(ABCD\) có cạnh là \(a\). Gọi \(E,{\rm{ }}F,{\rm{ }}G,{\rm{ }}H\) lần lượt là trung điểm \(AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA\).
Khi đó hình vuông \[EFGH\] có các đỉnh là trung điểm của các cạnh hình vuông \(ABCD\).
\(EF = \sqrt {B{E^2} + B{F^2}} = \sqrt {{{\left( {\frac{{BA}}{2}} \right)}^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{{a^2}}}{4}} = \frac{{\sqrt 2 a}}{2}\)
Khi đó \(\frac{{{S_{ABCD}}}}{{{S_{EFGH}}}} = \frac{{A{B^2}}}{{E{F^2}}} = \frac{{{a^2}}}{{\frac{{{a^2}}}{2}}} = 2\)
\( \Rightarrow {S_{ABCD}} = 2{S_{EFGH}}\).
Quay lại bài toán, gọi \({S_1};{\rm{ }}{S_2};{\rm{ }}{S_3};{\rm{ }}{S_4};{\rm{ }}{S_5};{\rm{ }}{S_6};{\rm{ }}{S_7}\) lần lượt là điện tích của các hình vuông \(1;{\rm{ 2}};{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7\)
Theo nhận xét, ta có: Diện tích hình vuông bất kì bằng hai lần diện tích hình vuông có các đỉnh là trung điểm của các cạnh hình vuông đã cho.
Do đó ta có:
\({S_5} = 2{S_6} = 2.2{S_7} = 4{S_7} = 4.32 = 128\) \(\left( {c{m^2}} \right)\)
Vậy diện tích hình vuông thứ 5 là 128 \(c{m^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.