Giải phương trình và hệ phương trình sau:

a)  \({x^2} + 2x - 3 = 0\)                                       

b)  \(\left\{ {\begin{array}{*{20}{c}}{ - x + 3y = 5}\\{x + y = 3}\end{array}} \right.\)

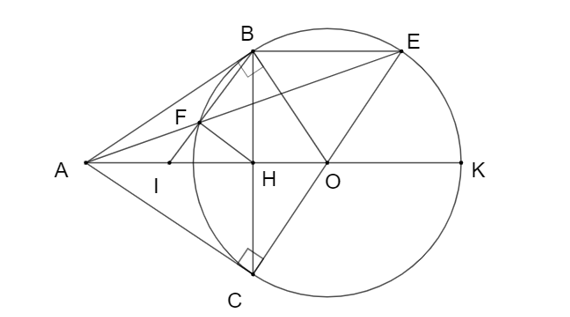
a) Xét tứ giác \(ABOC\) có:

\(\widehat {ABO} = \widehat {ACO} = 90^\circ \) (\(AB\), \(AC\) lần lượt là tiếp tuyến tại \(B\), \(C\) của \(\left( O \right)\))

\( \Rightarrow \widehat {ABO} + \widehat {ACO} = 180^\circ \)

Vậy tứ giác \(ABOC\) nội tiếp (Hai góc đối bù nhau)

b) Xét \(\Delta ABF\) và \(\Delta AEB\) có:

\(\widehat {BAF}\) là góc chung

\(\widehat {ABF} = \widehat {AEB}\)

Do đó \(\Delta ABF \sim \Delta AEB\) (g – g)

\[ \Rightarrow \frac{{AB}}{{AF}} = \frac{{AE}}{{AB}}\] (tính chất hai tam giác đồng dạng)

\( \Rightarrow A{B^2} = AE.AF\)

c) Xét \(\left( O \right)\) có \(AB\), \(AC\) lần lượt là tiếp tuyến tại \(B\), \(C\) của \(\left( O \right)\), \(OA \cap BC = H\)

\( \Rightarrow OA \bot BC\) tại \(H\)

Xét \(\Delta ABO\) vuông tại \(B\), đường cao \(BH\), ta có:

\(A{B^2} = AH.AO\)

Do đó \(AE.AF = AH.AO\) \(\left( { = A{B^2}} \right)\)

\( \Rightarrow \frac{{AE}}{{AH}} = \frac{{AO}}{{AF}}\)

Xét \(\Delta AEO\) và \(\Delta AHF\), ta có:

\(\widehat {HAF}\) là góc chung

\(\frac{{AE}}{{AH}} = \frac{{AO}}{{AF}}\)

Do đó \(\Delta AEO \sim \Delta AHF\) (c – g – c)

\( \Rightarrow \widehat {AEO} = \widehat {AHF}\) (Hai góc tương ứng)

Mà \(\widehat {AHF} + \widehat {FHO} = 180^\circ \) (hai góc kề bù)

nên \(\widehat {AEO} + \widehat {FHO} = 180^\circ \) hay \(\widehat {FEO} + \widehat {FHO} = 180^\circ \)

Suy ra tứ giác \(OHFE\) nội tiếp (Hai góc đối bù nhau)

\( \Rightarrow \widehat {HFE} + \widehat {HOE} = 180^\circ \) (Tính chất tứ giác nội tiếp)

Kéo dài \(AO\) cắt \(\left( O \right)\) tại \(K\) (\(O\) nằm giữa \(A\) và \(K\)ta có:\(\widehat {KOE} + \widehat {HOE} = 180^\circ \)              

\( \Rightarrow \widehat {KOE} = \widehat {HFE}\) (Cùng bù \(\widehat {HOE}\))

Xét \(\left( O \right)\), ta có:

\(\widehat {EBC} = 90^\circ \) (Góc nội tiếp chắn nửa đường tròn)

       \[ \Rightarrow EB \bot BC\]

Mặt khác, ta có:\( \Rightarrow OA \bot BC\) tại \(H\) (cmt)\( \Rightarrow AK \bot BC\)

Do đó: \(EB{\rm{ // }}AK\) (cùng vuông góc với \(BC\)) \( \Rightarrow \widehat {KOE} = \widehat {OEB}\) (Hai góc so le trong)

\( \Rightarrow \widehat {KOE} = \widehat {CEB}\)

Suy ra\(\widehat {HFE} = \widehat {CEB}{\rm{ }}\left( { = \widehat {KOE}} \right)\)

Xét \(\left( O \right)\), ta có: \(\widehat {BFE} = \widehat {BCE}\)

Trong \(\Delta EBC\) vuông tại \(B\), ta có: \(\widehat {BEC} + \widehat {BCE} = 90^\circ \)

Ta có:

\(\widehat {BFH} = \widehat {BFE} + \w\(HF\)idehat {HFE} = \widehat {BCE} + \widehat {BEC} = 90^\circ \)\( \Rightarrow HF \bot BI\) tại \(F\)

Xét \(\Delta BHI\) vuông tại \(H\), đường cao , ta có:

\(I{H^2} = IF.IB\) \(\left( 1 \right)\)

Xét \[\Delta IAF\] và \[\Delta IBA\], ta có:

\(\widehat {AIF}\) là góc chung

\(\widehat {IBA} = \widehat {IAF}\) (\(\widehat {IBA} = \widehat {BEF}\) cùng chắn cung \(BF\) của \(\left( O \right)\), \(\widehat {BEF} = \widehat {IAF}\)là hai góc so le trong của \(EB{\rm{ // }}AK\))

Vậy \[\Delta IAF \sim \Delta IBA\] (g – g)

\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{IF}}{{IA}}\)

\( \Rightarrow I{A^2} = IF.IB\) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow I{H^2} = I{A^2}\)

\( \Rightarrow IH = IA\) hay \(I\) là trung điểm \(AH\)

Nhận xét:

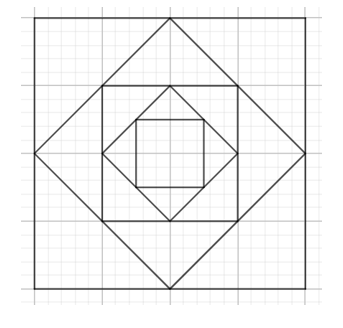
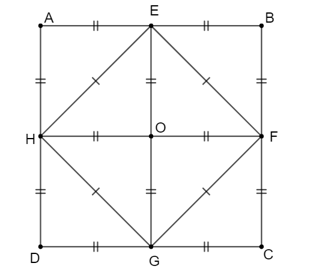
Xét hình vuông \(ABCD\), gọi \(E,{\rm{ }}F,{\rm{ }}G,{\rm{ }}H\) lần lượt là trung điểm \(AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA\).

Khi đó hình vuông \[EFGH\] có các đỉnh là trung điểm của các cạnh hình vuông \(ABCD\)

Dễ dàng nhận thấy\(\Delta AEH = \Delta BEH = \Delta CGF = \Delta DGH = \Delta OEH = \Delta OEF = \Delta OGF = \Delta OHG\) (c – c – c) (hoặc trường hợp hai cạnh góc vuông)

Do đó \({S_{ABCD}} = 8.{S_{\Delta OHG}}\), \({S_{EFGH}} = 4.{S_{\Delta OHG}}\)

\( \Rightarrow {S_{ABCD}} = 2{S_{EFGH}}\)

Quay lại bài toán, gọi \({S_1};{\rm{ }}{S_2};{\rm{ }}{S_3};{\rm{ }}{S_4};{\rm{ }}{S_5};{\rm{ }}{S_6};{\rm{ }}{S_7}\) lần lượt là điện tích của các hình vuông \(1;{\rm{ 2}};{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7\)

Theo nhận xét, ta có: Diện tích hình vuông bất kì bằng hai lần diện tích hình vuông có các đỉnh là trung điểm của các cạnh hình vuông đã cho.

Do đó ta có:

\({S_5} = 2{S_6} = 2.2{S_7} = 4{S_7} = 4.32 = 128\) \(\left( {c{m^2}} \right)\)

Vậy diện tích hình vuông thứ 5 là 128 \(c{m^2}\)

Cách khác:

Nhận xét:

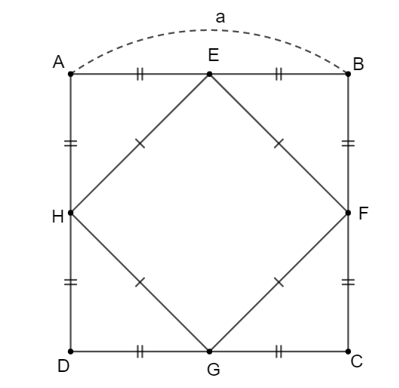
Xét hình vuông \(ABCD\) có cạnh là \(a\). Gọi \(E,{\rm{ }}F,{\rm{ }}G,{\rm{ }}H\) lần lượt là trung điểm \(AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA\).

Khi đó hình vuông \[EFGH\] có các đỉnh là trung điểm của các cạnh hình vuông \(ABCD\).

\(EF = \sqrt {B{E^2} + B{F^2}}  = \sqrt {{{\left( {\frac{{BA}}{2}} \right)}^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}}  = \sqrt {\frac{{{a^2}}}{4} + \frac{{{a^2}}}{4}}  = \frac{{\sqrt 2 a}}{2}\)

Khi đó \(\frac{{{S_{ABCD}}}}{{{S_{EFGH}}}} = \frac{{A{B^2}}}{{E{F^2}}} = \frac{{{a^2}}}{{\frac{{{a^2}}}{2}}} = 2\)

\( \Rightarrow {S_{ABCD}} = 2{S_{EFGH}}\).

Quay lại bài toán, gọi \({S_1};{\rm{ }}{S_2};{\rm{ }}{S_3};{\rm{ }}{S_4};{\rm{ }}{S_5};{\rm{ }}{S_6};{\rm{ }}{S_7}\) lần lượt là điện tích của các hình vuông \(1;{\rm{ 2}};{\rm{ }}3;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7\)

Theo nhận xét, ta có: Diện tích hình vuông bất kì bằng hai lần diện tích hình vuông có các đỉnh là trung điểm của các cạnh hình vuông đã cho.

Do đó ta có:

\({S_5} = 2{S_6} = 2.2{S_7} = 4{S_7} = 4.32 = 128\) \(\left( {c{m^2}} \right)\)

Vậy diện tích hình vuông thứ 5 là 128 \(c{m^2}\)