Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hải Phòng
420 người thi tuần này 4.6 737 lượt thi 34 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề thi thử TS vào 10 (Tháng 1) năm học 2025 - 2026_Môn Toán_THCS Cầu Giấy_Quận Cầu Giấy
3.8 K lượt thi
13 câu hỏi
123 bài tập Nón trụ cầu và hình khối có lời giải
4 K lượt thi
123 câu hỏi
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
2.2 K lượt thi
24 câu hỏi
52 bài tập Hệ thức lượng trong tam giác có lời giải
1.9 K lượt thi
52 câu hỏi
63 bài tập Tỉ số lượng giác và ứng dụng có lời giải
1.7 K lượt thi
63 câu hỏi
41 bài tập Bất đẳng thức và bất phương trình bậc nhất 1 ẩn có lời giải
1.7 K lượt thi
41 câu hỏi
35 bài tập Đa giác đều. Phép quay có lời giải
1.4 K lượt thi
35 câu hỏi
Đề thi thử TS vào 10 (Tháng 4) năm học 2025 - 2026_Môn Toán_THPT Chu Văn An_Tỉnh Thái Nguyên
1.8 K lượt thi
13 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. 9.
B. \[ - 9.\]
C. \( \pm 9.\)
D. \[6\,\,561.\]
Lời giải
Đáp án đúng là: A
Căn bậc hai số học của 81 là 9 vì \({9^2} = 81.\)
Câu 2
A. Điểm \(C'\left( {2\,;\, - 4} \right)\) và \(C' \notin \left( P \right)\).
B. Điểm \(C'\left( { - 2\,;\,4} \right)\) và \(C' \in \left( P \right)\).
C. Điểm \(C'\left( { - 2\,;\,4} \right)\) và \(C' \notin \left( P \right)\).
D. Điểm \(C'\left( {4\,;\, - 2} \right)\) và \(C' \in \left( P \right)\).
Lời giải
Đáp án đúng là: B
Đồ thị hàm số \(y = a{x^2},\) với \(a \ne 0\) đối xứng qua trục \(Oy\) nên điểm \(C'\) đối xứng với điểm \(C\) qua trục tung \[Oy\] thì \(C' \in \left( P \right)\) và \({x_{C'}} = - {x_C};\,\,{y_{C'}} = {y_C}\) nên \(C'\left( { - 2\,;\,4} \right)\).
Câu 3
A. \({x^2}\sqrt 2 + 3x - 2 = 0\).
B. \(2{x^2} + 3\sqrt x - 2 = 0\).
C. \({x^2} \cdot \sqrt 2 + \frac{3}{x} - 2 = 0\).
D. \({x^2} \cdot \sqrt 2 + 3x - \frac{2}{{{x^2}}} = 0\).
Lời giải
Đáp án đúng là: A
Phương trình bậc hai một ẩn có dạng \(a{x^2} + bx + c = 0\) với \(a \ne 0.\)
Do đó phương trình bậc hai một ẩn trong các phương án ở trên là \({x^2}\sqrt 2 + 3x - 2 = 0\).
Câu 4
A. \( - 2025a + 1 < - 2025b + 2\).
B. \(2025a + 1 > 2025b + 2\).
C. \( - 2025a < - 2025b - 2\).
D. \(2025a + 1 < 2025b + 2\).
Lời giải
Đáp án đúng là: D
Vì \(a < b\) nên \(2025a < 2025b\), suy ra \(2025a + 1 < 2025b + 1 < 2025b + 2\).
Vậy ta chọn phương án D.
Câu 5
A. \(\left( {\frac{3}{2}\,;\,3} \right)\).
B. \(\left( {3\,;\,\frac{3}{2}} \right)\).
C. \(\left( {3\,;\,\frac{2}{3}} \right)\).
D. \(\left( {\frac{2}{3}\,;\,3} \right)\).
Lời giải
Đáp án đúng là: B
Sử dụng máy tính cầm tay, ta lần lượt bấm các phím
Trên màn hình hiện lên kết quả \(x = 3;\) ấn tiếp phím màn hình hiện kết quả \(y = \frac{3}{2}.\)
Vậy nghiệm của hệ phương trình đã cho là \(\left( {3;\,\,\frac{3}{2}} \right).\) Ta chọn phương án B.
Câu 6
A. Đường tròn có vô số tâm đối xứng và chỉ có một trục đối xứng.
B. Đường tròn chỉ có một tâm đối xứng và có vô số trục đối xứng.
C. Đường tròn chỉ có một tâm đối xứng và một trục đối xứng.
D. Đường tròn có vô số tâm đối xứng và vô số trục đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
![Phép quay thuận chiều tâm \(O\) biến điểm \(M\) thành điểm \(Q\) thì các điểm \[N,\,\,P,\,\,Q\] tương ứng thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/17-1741707775.png)
A. \[P,{\rm{ }}N,\,\,M\].
B. \[M,{\rm{ }}N,{\rm{ }}P\].
C. \[M,{\rm{ }}N,{\rm{ }}P\].
D. \[P,{\rm{ }}M,{\rm{ }}N\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Độ dài cạnh \[AC\] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/18-1741707855.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ \).
B. \(BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ \).
C. \(BM = 4\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 30^\circ \).
D. \(BM = 8\;{\rm{cm}};{\rm{ }}\widehat {AMO} = 60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
![Số tiền mà doanh nghiệp cần chi để sản xuất \[1\,\,000\] thùng tôn là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/21-1741708029.png)
A. \[323\,\,238\,\,000.\]
B. \[223\,\,238\,\,000.\]
C. \[123\,\,238\,\,000.\]
D. Đáp án khác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right);\,\,\left( {N,\,N} \right)\].
B. \(\left( {S,S} \right);\,\,\left( {N,N} \right)\).
C. \(\left( {S,N} \right);\,\,\left( {N,S} \right)\).
D. \(\left( {S,\,S} \right);\,\,\left( {S,\,N} \right);\,\,\left( {N,\,S} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(20\% \).
B. \(10\% \).
C. \(8\% \).
D. \(6\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
PHẦN II. Câu hỏi trắc nghiệm đúng sai.
Một trường trung học cơ sở mua 500 quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai \(\left( {x,y \in \mathbb{N}*} \right)\) để làm phần thưởng cho học sinh. Giá bán của mỗi quyển vở loại thứ nhất, loại thứ hai lần lượt là \[8\,\,000\] đồng và \[9\,\,000\] đồng. Biết tổng số tiền nhà trường đã dùng để mua 500 quyển vở đó là \[4\,\,200\,\,000\] đồng. Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; các học sinh khác không được thưởng và số học sinh này chiếm \(40\% \) tổng số học sinh cả trường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Một chiếc áo có giá niêm yết là \[120\,\,000\] đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá \(x\% \) so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá \(x\% \) so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
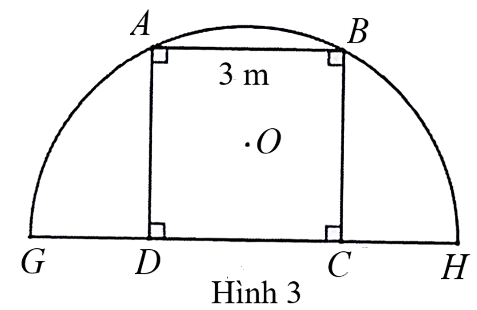
Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính \[FA\] (như hình 3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Một hộp chứa 15 quả cầu màu xanh được đánh số từ 1 đến 15 và 5 quả cầu màu đỏ được đánh số từ 16 đến 20. Lấy ngẫu nhiên một quả cầu trong hộp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo