Câu hỏi:
12/03/2025 198
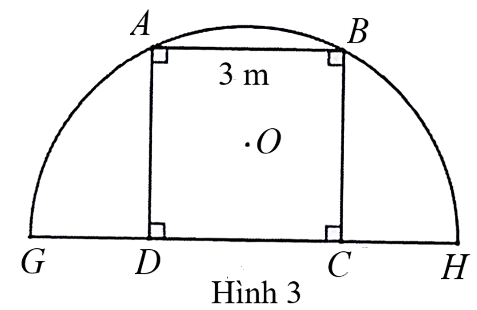
Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính \[FA\] (như hình 3).
a) Độ dài đoạn thẳng \[OA\] là \(1,5\sqrt 2 \;\,{\rm{m}}\).
Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính \[FA\] (như hình 3).
Quảng cáo
Trả lời:
Giải bởi Vietjack
![a) Độ dài đoạn thẳng \[OA\] là \(1,5\sqrt 2 \;\,{\rm{m}}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/23-1741709121.png)
Sai
Ta có \[ABCD\] là hình vuông nên \(\widehat {ABC} = \widehat {ADC} = 90^\circ \) và \(BC = CD = AD = AB = 3{\rm{\;m}}\).
Xét \(\Delta ABC\) vuông tại \(B\), theo định lí Pythagore, ta có:
\(A{C^2} = A{B^2} + A{C^2} = {3^2} + {3^2} = 18.\)
Suy ra \(AC = \sqrt {18} = 3\sqrt 2 {\rm{\;(m)}}{\rm{.}}\)
Do đó \(AO = \frac{1}{2}AC = \frac{1}{2} \cdot 3\sqrt 2 = 1,5\sqrt 2 {\rm{\;(m)}}{\rm{.}}\)Câu hỏi cùng đoạn
Câu 2:
b) Độ dài đoạn thẳng .
Lời giải của GV VietJack
Đúng
Ta có \(F\) là trung điểm của \(CD\) nên \(FD = FC = \frac{1}{2}DC = \frac{1}{2} \cdot 3 = 1,5{\rm{\;(m)}}{\rm{.}}\)
Xét \(\Delta ADF\) vuông tại \(D\), theo định lí Pythagore, ta có:
\(F{A^2} = A{D^2} + D{F^2} = {3^2} + 1,{5^2} = 11,25\).
Suy ra \(FA = \sqrt {11,25} = 1,5\sqrt 5 {\rm{\;(m)}}{\rm{.}}\)
Do đó \(HG = 2FA = 2 \cdot 1,5\sqrt 5 = 3\sqrt 5 {\rm{\;(m)}}{\rm{.}}\)
Câu 3:
c) Độ dài cung \[GAH\] là \(3\sqrt 5 \pi \,\,{\rm{m}}\).
Lời giải của GV VietJack
Đúng
Độ dài cung \[GAH\] là \(\pi \cdot FA = \pi \cdot 1,5\sqrt 5 = 1,5\sqrt 5 \pi {\rm{\;(m)}}{\rm{.}}\)
Câu 4:
d) Người ta muốn sơn toàn bộ nửa hình tròn (không sơn phần cổng \[ABCD).\] Giá tiền sơn \(30\,\,000\) đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\) Biết \(\pi = 3,14\) kết quả làm tròn đến nghìn đồng. Số tiền sơn là \[1\,\,059\] (nghìn đồng).
Lời giải của GV VietJack
Sai
Diện tích cần sơn là \(\frac{1}{2}\pi \cdot F{A^2} - {S_{ABCD}} = \frac{1}{2} \cdot 3,14 \cdot {\left( {1,5\sqrt 5 } \right)^2} - {3^2} = 8,6625{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Số tiền sơn là \(8,6625 \cdot 30\,\,000 \approx 260\,\,000\) (đồng).
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xác suất lấy được quả cầu màu xanh là \(\frac{{15}}{{20}} = 0,75\).
Xác suất lấy được quả cầu màu đỏ là \(\frac{5}{{20}} = 0,25\).
Ta thấy \(0,75 \ne 0,25\) nên khẳng định a) là sai.
Lời giải
Đúng
Giá của chiếc áo sau lần giảm giá thứ nhất là \(120\,\,000 - 120\,\,000 \cdot x\% = 120\,\,000 - 1\,\,200x\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa