Đề thi thử TS vào 10 (Tháng 4) năm học 2025 - 2026_Môn Toán_THPT Chu Văn An_Tỉnh Thái Nguyên
62 người thi tuần này 4.6 1.7 K lượt thi 13 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL THCS Văn Quán - HN_năm học 2025-2026_Tháng 12 có đáp án
148 lượt thi
6 câu hỏi
Đề KSCL THCS Phú Diễn - HN_năm học 2025-2026_Tháng 12 có đáp án
94 lượt thi
5 câu hỏi
Đề KSCL THCS Lê Lợi - HN_năm học 2025-2026_Tháng 12 có đáp án
110 lượt thi
8 câu hỏi
Đề KSCL THCS Thịnh Quang - HN_năm học 2025-2026_Tháng 9 có đáp án
130 lượt thi
6 câu hỏi
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
146 lượt thi
30 câu hỏi
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
126 lượt thi
10 câu hỏi
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
118 lượt thi
11 câu hỏi
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
132 lượt thi
13 câu hỏi
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
1) Giải phương trình: \(3{x^2} - 7x + 2 = 0\)
Phương trình có \(\Delta = {\left( { - 7} \right)^2} - 4 \cdot 3 \cdot 2 = 25 > 0\) và \(\sqrt \Delta = \sqrt {25} = 5.\)
Do đó, phương trình đã cho có hai nghiệm phân biệt là:
\({x_1} = \frac{{7 + 5}}{{2 \cdot 3}} = 2;\,\,{x_1} = \frac{{7 - 5}}{{2 \cdot 3}} = \frac{1}{3}.\)
2) Xét hệ phương trình \(\left\{ \begin{array}{l}x - 3y = 5\,\,\,\,\,\,\,\,\,\left( 1 \right)\\3x + 2y = 4\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\)
Từ phương trình (1) của hệ ta có \(x = 3y + 5\,\,\,(3),\) thế vào phương trình (2) của hệ, ta được:
\[3\left( {3y + 5} \right) + 2y = 4\] hay \(11y = - 11,\) suy ra \(y = - 1.\)
Thay \(y = - 1\) vào phương trình (3), ta được:
\(x = 3 \cdot \left( { - 1} \right) + 5 = 2.\)
Vậy hệ phương trình đã cho có nghiệm là \(\left( {2;\,\, - 1} \right).\)
Đoạn văn 1
Câu 2-3. (1,0 điểm) Cho biểu thức với \(x \ge 0,\,\,x \ne 1.\)
Lời giải
a) Với \(x \ge 0,x \ne 1,\) ta có:
\(P = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{x - 1}}\)
\( = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{3}{{\sqrt x + 1}} - \frac{{6\sqrt x - 4}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{3\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{6\sqrt x - 4}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x + \sqrt x + 3\sqrt x - 3 - 6\sqrt x + 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)
\( = \frac{{x - 2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}.\)
Vậy khi \(x \ge 0,\,\,x \ne 1\) thì \(P = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}.\)
Lời giải
b) Với điều kiện \(x \ge 0,\,\,x \ne 1\) ta có:
\(P = \frac{1}{3}\) khi \(\frac{{\sqrt x - 1}}{{\sqrt x + 1}} = \frac{1}{3}\) hay \(3\left( {\sqrt x - 1} \right) = \sqrt x + 1\) nên \(2\sqrt x = 4,\) suy ra \(x = 4.\)
Giá trị \(x = 4\) thỏa mãn điều kiện \(x \ge 0,\,\,x \ne 1.\)
Vậy \(P = \frac{1}{3}\) khi \(x = 4.\)
Đoạn văn 2
Câu 4-5. (1,0 điểm) Một cây cầu treo có trụ tháp đôi cao 75 m so với mặt của cây cầu và cách nhau 400 m. Các dây cáp có dạng đồ thị của hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) như hình bên và được treo trên đỉnh tháp.
Lời giải
a) Vì đồ thị hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) đi qua điểm \(B\left( {200;\,\,75} \right)\) nên thay \(x = 200;y = 75\) vào công thức \(y = a{x^2}\,\,\left( {a \ne 0} \right),\) ta được:
\(75 = a \cdot {200^2}\) suy ra \(a = \frac{3}{{1\,\,600}}.\)
Lời giải
b) Với \(a = \frac{3}{{1\,\,600}},\) ta có hàm số là \(y = \frac{3}{{1\,\,600}}{x^2}.\)
Điểm \(H\) thuộc đồ thị hàm số trên và có hoành độ 100 nên thay \(x = 100\) vào công thức hàm số \(y = \frac{3}{{1600}}{x^2},\) ta được:
\(y = \frac{3}{{1\,\,600}} \cdot {100^2} = 18,75.\)
Vậy chiều \[CH\] của dây cáp là \(18,75\) m.
Đoạn văn 3
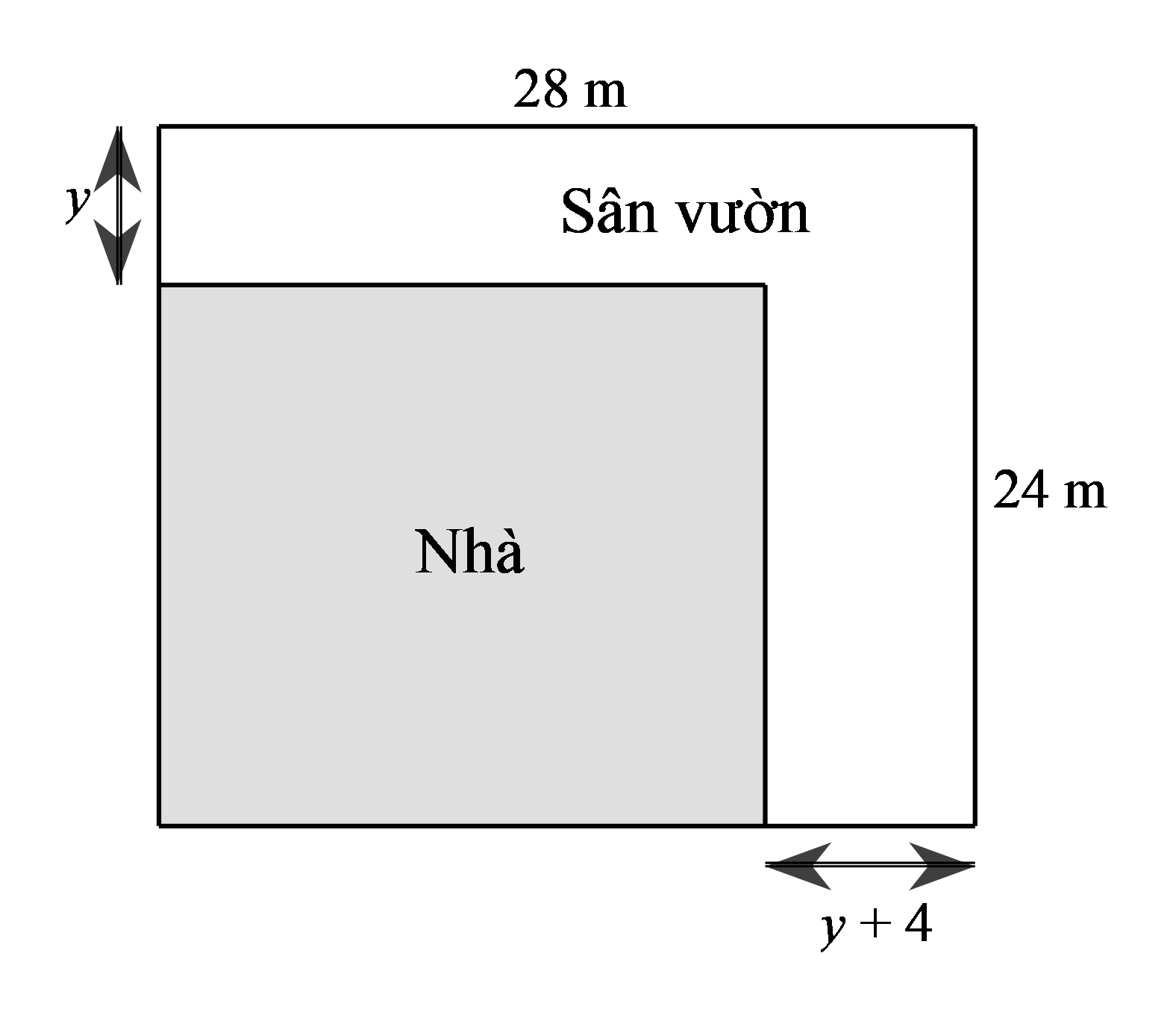
Câu 6-7. (1,0 điểm) Bác Nam có một mảnh đất hình chữ nhật với chiều dài 28 m và chiều rộng 24 m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn (như hình vẽ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Câu 8-9 . (1,5 điểm) Thống kê điểm kiểm tra giữa học kì II môn Toán của 40 học sinh lớp 9A được kết quả như sau:
|
Điểm |
5 |
6 |
7 |
8 |
9 |
|
Số học sinh |
4 |
8 |
10 |
12 |
6 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Câu 10-11. (2,0 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Câu 12-13. (1,5 điểm) Cho tam giác \(ABC\) \(\left( {AB < AC} \right)\) có \(AH\) là đường cao. Đường tròn tâm \(O\) đường kính \[BH\] cắt \(AB\) tại \(D\) và đường tròn tâm \(O'\) đường kính \(HC\) cắt \(AC\) tại \(E.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập