Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 13
53 người thi tuần này 4.6 112 lượt thi 9 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
Bảng tần số ghép nhóm
|
Chiều cao (cm) |
[155; 158) |
[158; 161) |
[161; 164) |
[164;167) |
|
Số HS |
5 |
12 |
15 |
8 |
· Tần số tương đối của nhóm [161; 164) là
. 100% = 37,5%Lời giải
|
2) Kí hiệu các quả bóng đỏ trắng xanh là Đ1, Đ2, X1, X2, T1, T2 Không gian mẫu: Ω = { Đ1Đ2, X1X2, T1T2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2, X1T1, X1T2, X2T1, X2T2} |
|
Có 9 kết quả thuận lợi cho biến cố A là : Đ1Đ2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2 |
|
P(A) = |
Lời giải
|
1) Bảng tần số ghép nhóm
|
||||||||||
|
1) Thay \[x = 16\](tmđk) vào biểu thức \[A = \frac{{3\sqrt x - 2}}{{1 - \sqrt x }}\]ta được \[A = \frac{{3\sqrt {16} - 2}}{{1 - \sqrt {16} }} = \frac{{3.4 - 2}}{{1 - 4}} = \frac{{12 - 2}}{{ - 3}} = - \frac{{10}}{3}\] Vậy khi \[x = 16\]thì \[A = - \frac{{10}}{3}\] |
||||||||||
|
2) Với x ≥ 0 , x ≠ 1 . Ta có: \[P = A + B = \frac{{3\sqrt x - 2}}{{1 - \sqrt x }} + \frac{{15\sqrt x - 11}}{{x + 2\sqrt x - 3}} - \frac{{2\sqrt x + 3}}{{\sqrt x + 3}}\] \[P = \frac{{\left( { - 3\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} + \frac{{15\sqrt x - 11}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} - \frac{{\left( {2\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\] \[P = \frac{{ - 3x - 7\sqrt x + 6 + 15\sqrt x - 11 - 2x - \sqrt x + 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\]\[ = \frac{{ - 5x + 7\sqrt x - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} = \frac{{ - \left( {\sqrt x - 1} \right)\left( {5\sqrt x - 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\] \[P = \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}}\] . Vậy với \[x \ge 0;\,x\, \ne \,1\] thì \[P = \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}}\]
|
||||||||||
|
Có 9 kết quả thuận lợi cho biến cố A là : Đ1Đ2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2 |
||||||||||
|
3) Với \[x \ge 0;\,x\, \ne \,1\] ta có: \[m = P\left( {\sqrt x + 3} \right) = \frac{{ - 5\sqrt x + 2}}{{\sqrt x + 3}}.\left( {\sqrt x + 3} \right) = - 5\sqrt x + 2\] Với \[x \ge 0 \Rightarrow - 5\sqrt x \le 0 \Rightarrow - 5\sqrt x + 2 \le 2 \Rightarrow m \le 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\] Mặt khác \[x\, \ne \,1\, \Rightarrow \,\sqrt x \, \ne 1\, \Rightarrow - 5\sqrt x \ne - 5 \Rightarrow - 5\sqrt x + 2 \ne - 3 \Rightarrow m \ne - 3\,\,\left( 2 \right)\] Từ (1) và (2) \[ \Rightarrow m \le 2;\,m \ne \, - 3\] Vậy với \[m \le 2;\,m\, \ne \, - 3\] thì có x thỏa mãn \[P\left( {\sqrt x + 3} \right) = m\] |
Lời giải
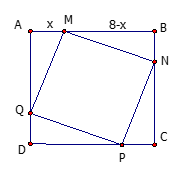
Gọi cái sân đó là hình vuông ABCD, phần nát gạch màu trang trí là hình vuông MNPQ
Chứng minh
Gọi AM = x thì MB = 8-x
Diện tích hình vuông MNPQ có diện tích nhỏ nhất khi tổng diện tích 4 tam giác vuông ở 4 góc hình vuông ABCD là lớn nhất. Gọi S là tổng diện tích 4 tam giác đó, ta có:
S = 2. AM. AQ
Mà AM + AQ = AM + MB = 8 (m)
(AM – MB)2
AM2 + MB2
(AM + MB)2
= 32
Hay S
Dấu “=” xảy ra khi AM = MB =
Khi đó M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vậy khi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA thì hình vuông MNPQ có diện tích nhỏ nhất.Đoạn văn 2
Lời giải
|
Đổi 30 phút = 1/2 giờ Gọi vận tốc riêng của ca nô là x(km/h) (x > 3) Vận tốc xuôi dòng là x + 3 (km/h) Vận tốc ngược dòng là x - 3 (km/h) |
|
Thời gian xuôi dòng là Thời gian ngược dòng là Thời gian cả đi và về và nghỉ là: 10 giờ 36 phút - 6 giờ 30 phút = 4 giờ 06 phút = |
|
Ta có phương trình: = . Giải phương trình ra x1 = 27; x2 = |
|
Đối chiếu điều kiện và trả lời Vận tốc riêng của ca nô là 27 km/h |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.