(4,0 điểm)
Một bồn nước inox có dạng một hình trụ với chiều cao 1,75 m và bán kính đáy là 5 dm. Trong bồn đang chứa đầy nước, người ta tháo nước ở trong bồn ra cho đến khi mực nước trong bồn còn cao 1m. Hỏi số nước đã tháo ra ngoài là bao nhiêu lít? (Bỏ qua bề dày của bồn nước).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 13 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Đổi 1,75m = 17,5 dm Số nước đã tháo ra ngoài thể tích của hình trụ có bán kính ddáy là 5 dm và có chiều cao là: 17,5dm – 10dm = 7,5dm |
|
Thể tích phần nước tháo ra là 2.5.π .7,5 235,5 dm3 = 235,5 l Vậy thể tích nước đã tháo ra ngoài xấp xỉ 235,5 lít |
Câu hỏi cùng đoạn
Câu 2:
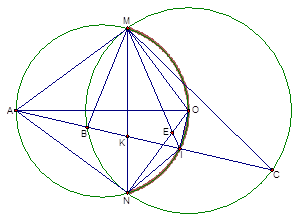
Cho đường tròn (O) cố định. Từ một điểm A cố định ở bên ngoài đường tròn (O), kẻ các tiếp tuyến AM và AN với đường tròn ( M;N là các tiếp điểm). Đường thẳng đi qua A cắt đường tròn (O) tại hai điểm B và C (B nằm giữa A và C). Gọi I là trung điểm của dây BC.
a) . Chứng minh rằng: AMON là tứ giác nội tiếp.
b). Gọi K là giao điểm của MN và BC. Chứng minh rằng: AK.AI = AB.AC
c). Xác định vị trí của cát tuyến ABC để \(IM = 2IN\).
Cho đường tròn (O) cố định. Từ một điểm A cố định ở bên ngoài đường tròn (O), kẻ các tiếp tuyến AM và AN với đường tròn ( M;N là các tiếp điểm). Đường thẳng đi qua A cắt đường tròn (O) tại hai điểm B và C (B nằm giữa A và C). Gọi I là trung điểm của dây BC.
a) . Chứng minh rằng: AMON là tứ giác nội tiếp.
b). Gọi K là giao điểm của MN và BC. Chứng minh rằng: AK.AI = AB.AC
c). Xác định vị trí của cát tuyến ABC để \(IM = 2IN\).
Giải bởi Vietjack
|
a) Tứ giác AMON nội tiếp Vì AM là tiếp tuyến nên AM MO Do đó vuông tại M nên nội tiếp trong đường tròn đường kính AO Chứng minh tương tự ta được nội tiếp trong đường tròn đường kính AO Do đó 4 điểm A, O, M, N cùng nằm trên đường tròn đường kính AO Vậy tứ giác AMON nội tiếp |
|
b) Chứng minh I thuộc đường tròn đường kính AO Chứng minh Chứng minh Từ (1) và (2) suy ra AK.AI = AB.AC
|
|
c) Chứng minh Chứng minh (vì NA=MA) Do đó \(IM = 2IN \Leftrightarrow \frac{{IN}}{{IM}} = \frac{1}{2} \Leftrightarrow \frac{{\frac{{KN.MA}}{{KA}}}}{{\frac{{KM.MA}}{{KA}}}} = \frac{1}{2} \Leftrightarrow \frac{{KN}}{{KM}} = \frac{1}{2}\) Vậy IM=2.IN khi cát tuyến ABC cắt MN tại K với \(\frac{{KN}}{{KM}} = \frac{1}{2}\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Đổi 30 phút = 1/2 giờ Gọi vận tốc riêng của ca nô là x(km/h) (x > 3) Vận tốc xuôi dòng là x + 3 (km/h) Vận tốc ngược dòng là x - 3 (km/h) |
|
Thời gian xuôi dòng là Thời gian ngược dòng là Thời gian cả đi và về và nghỉ là: 10 giờ 36 phút - 6 giờ 30 phút = 4 giờ 06 phút = |
|
Ta có phương trình: = . Giải phương trình ra x1 = 27; x2 = |
|
Đối chiếu điều kiện và trả lời Vận tốc riêng của ca nô là 27 km/h |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bảng tần số ghép nhóm
|
Chiều cao (cm) |
[155; 158) |
[158; 161) |
[161; 164) |
[164;167) |
|
Số HS |
5 |
12 |
15 |
8 |
· Tần số tương đối của nhóm [161; 164) là
. 100% = 37,5%Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập