khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Ôn vào 10
  3. Toán

Câu hỏi:

29/12/2025 2,468 Lưu

(0,5 điểm) Một cái sân hình vuông ABCD có cạnh là 8 m. Người ta muốn lát gạch màu khác để trang trí lên mảnh sân hình vuông MNPQ nội tiếp trong sân hình vuông ABCD. Tìm vị trí của M, N, P, Q để hình vuông MNPQ có diện tích nhỏ nhất

Xem lời giải

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 13 !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

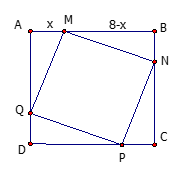
Media VietJack

Gọi cái sân đó là hình vuông ABCD, phần nát gạch màu trang trí là hình vuông MNPQ

Chứng minh

Gọi AM = x thì MB = 8-x

Diện tích hình vuông MNPQ có diện tích nhỏ nhất khi tổng diện tích 4 tam giác vuông ở 4 góc hình vuông ABCD là lớn nhất. Gọi S là tổng diện tích 4 tam giác đó, ta có:

S = 2. AM. AQ

Mà AM + AQ = AM + MB = 8 (m)

(AM – MB)2

AM2 + MB2

(AM + MB)2

= 32

Hay S

Dấu “=” xảy ra khi AM = MB =

Khi đó M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

Vậy khi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA thì hình vuông MNPQ có diện tích nhỏ nhất.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một bồn nước inox có dạng một hình trụ với chiều cao 1,75 m và bán kính đáy là 5 dm. Trong bồn đang chứa đầy nước, người ta tháo nước ở trong bồn ra cho đến khi mực nước trong bồn còn cao 1m. Hỏi số nước đã tháo ra ngoài là bao nhiêu lít? (Bỏ qua bề dày của bồn nước).

Lời giải

Đổi 1,75m = 17,5 dm

Số nước đã tháo ra ngoài thể tích của hình trụ có bán kính ddáy là 5 dm và có chiều cao là:

17,5dm – 10dm = 7,5dm

Thể tích phần nước tháo ra là

2.5.π .7,5  235,5 dm3 = 235,5 l

Vậy thể tích nước đã tháo ra ngoài xấp xỉ 235,5 lít

Câu 2

Lúc 6 giờ 30 phút sáng, một ca nô xuôi dòng sông từ A đến B dài 48km. Khi đến B, ca nô nghỉ 30 phút sau đó ngược dòng từ B về A lúc 10 giờ 36 phút cùng ngày. Tìm vận tốc riêng của ca nô biết vận tốc dòng nước là 3km/h.

Lời giải

Đổi 30 phút = 1/2 giờ

Gọi vận tốc riêng của ca nô là x(km/h) (x > 3)

Vận tốc xuôi dòng là x + 3 (km/h)

Vận tốc ngược dòng là x - 3 (km/h)

Thời gian xuôi dòng là

Thời gian ngược dòng là

Thời gian cả đi và về và nghỉ là: 10 giờ 36 phút - 6 giờ 30 phút = 4 giờ 06 phút =

Ta có phương trình:

= .

Giải phương trình ra x1 = 27; x2 =

Đối chiếu điều kiện và trả lời Vận tốc riêng của ca nô là 27 km/h

Câu 3

Đo chiều cao (đơn vị là cm) của học sinh lớp 9A cho kết quả như sau;

156             157      164      166      166      165       157      154      155      158      160      163       163

161             162      159      159      160      160       160      159      158      160      160      158       163

162             162      162      161      162      161       163      161      163      161      164      166       165

165

Hãy lập bảng tần số ghép nhóm với các nhóm [155; 158), [158; 161), [161; 164), [164;167).

Tính tần số tương đối của nhóm [161; 164)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

(1,5 điểm) Cho hai biểu thức \(A = \frac{{3\sqrt x  - 2}}{{1 - \sqrt x }}\) và \(B = \frac{{15\sqrt x  - 11}}{{x + 2\sqrt x  - 3}} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 3}}{\rm{ }}\) với  \(x \ge 0,x \ne 1\)

1) . Tính giá trị của biểu thức \(A\) khi \(x = 16\)

2) . Đặt \(P = A + B\). Rút gọn biểu thức \(P\)

3) . Tìm \(m\) để có x thỏa mãn \(P(\sqrt x  + 3) = m\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong túi có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả màu trắng, 2 quả màu xanh. Không nhìn vào túi mà lấy ra 2 quả bóng. Tính xác suất của biến cố A lấy được ít nhất một quả bóng màu đỏ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hai người thợ quét sơn một ngôi nhà. Nếu họ cùng làm thì trong 6 ngày xong việc. Nếu người thợ thứ nhất làm một mình trong 5 ngày rồi nghỉ, người thứ hai làm tiếp 4 ngày thì cả hai làm được  công việc. Hỏi nếu làm riêng thì mỗi người thợ phải làm trong bao nhiêu ngày để xong việc.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập