Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 44

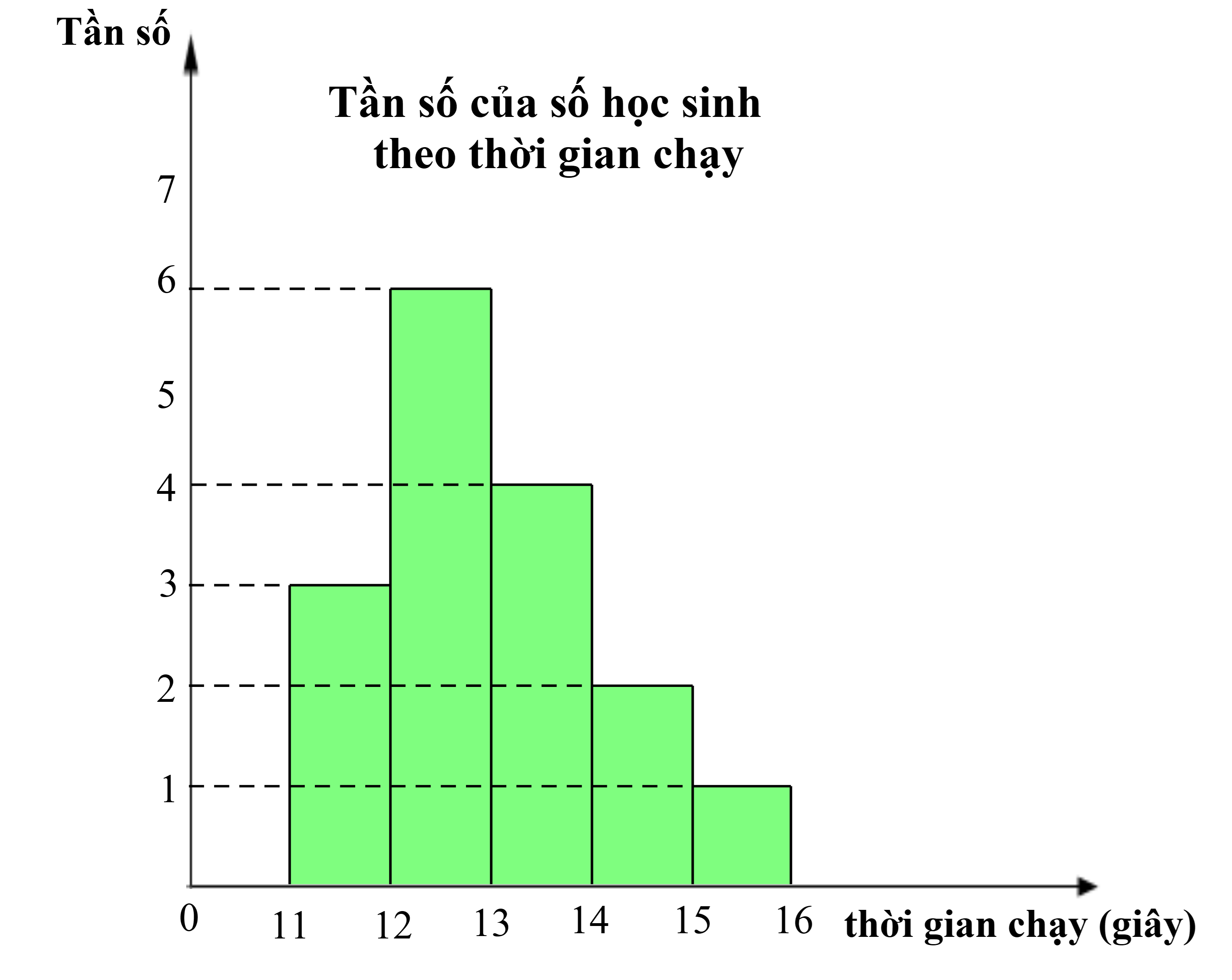
Có \[9\] học sinh chạy \[100\,{\rm{m}}\] hết ít hơn \[13\] giây.

Tần số tương đối ghép nhóm của nhóm \(\left[ {13;14} \right)\) là: \(\frac{4}{{3 + 6 + 4 + 2 + 1}} \cdot 100\%  = 25\% \)

Do \(n\) tấm thẻ cùng loại nên các thẻ có cùng khả năng đươc chọn. Có \(n\) kết quả có thể xảy ra.

Có \(9\) kết quả thuận lợi cho biến cố “Lấy được tấm thẻ ghi số có một chữ số”.

Vậy xác suất của biến cố “Lấy được tấm thẻ ghi số có một chữ số” là \(\frac{9}{n}\).

Ta có: \(\frac{9}{n} = 0,25\). Suy ra \(n = 36\).

Vậy bạn Long có \(36\) tấm thẻ.

1) Tính giá trị của biểu thúc \(A\) khi \(x = 16\).

Thay \(x = 16\) (tmđk) vào \(A\) ta có: \(A = \frac{{16}}{{\sqrt {16}  - 3}} = \frac{{16}}{{4 - 3}} = 16\)

Vậy với \(x = 16\) thì \(A = 16\).

2) Chứng minh \(B = \frac{{2\sqrt x  - 1}}{{\sqrt x  - 3}}\).

ĐKXĐ: \(x > 0,x \ne 9\)

\(\begin{array}{l}B = \frac{{2x - 3}}{{x - 3\sqrt x }} - \frac{1}{{\sqrt x }}\\B = \frac{{2x - 3}}{{\sqrt x \left( {\sqrt x  - 3} \right)}} - \frac{{\sqrt x  - 3}}{{\sqrt x \left( {\sqrt x  - 3} \right)}}\\B = \frac{{2x - \sqrt x }}{{\sqrt x \left( {\sqrt x  - 3} \right)}}\\B = \frac{{\sqrt x \left( {2\sqrt x  - 1} \right)}}{{\sqrt x \left( {\sqrt x  - 3} \right)}} = \frac{{2\sqrt x  - 1}}{{\sqrt x  - 3}}\end{array}\)

Vậy với \(x > 0,x \ne 9\) thì \(B = \frac{{2\sqrt x  - 1}}{{\sqrt x  - 3}}\).

3) Tìm tất cả giá trị của \(x\) để \(A - B < 0\).

\(A - B < 0\)

\(\frac{x}{{\sqrt x  - 3}} - \frac{{2\sqrt x  - 1}}{{\sqrt x  - 3}} < 0\)

\(\frac{{x - 2\sqrt x  + 1}}{{\sqrt x  - 3}} < 0\)

\(\frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\sqrt x  - 3}} < 0\)

Ta có: \({\left( {\sqrt x  - 1} \right)^2} \ge 0\)

Do đó:  \(\left\{ {\begin{array}{*{20}{l}}{\sqrt x  - 3 < 0}\\{\sqrt x  - 1 \ne 0}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{\sqrt x  < 3}\\{\sqrt x  \ne 1}\end{array}} \right.\)

\(\left\{ {\begin{array}{*{20}{l}}{x < 9}\\{x \ne 1}\end{array}} \right.\)

Kết hợp với điều kiện ta có: \(0 < x < 9\) và \(x \ne 1\)

Vây với \(0 < x < 9\) và \(x \ne 1\) thì \(A - B < 0\).

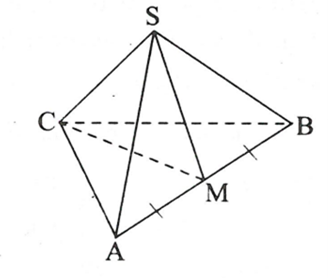
Gọi \[M\] là trung điểm của \[AB\].

Khi đó \[SM\] là trung đoạn của hình chóp.

Ta có \[AB = BC = AC = x\] thì:

\[S{M^2} = S{B^2} - {\left( {\frac{x}{2}} \right)^2} = {6^2} - \frac{{{x^2}}}{4}\]

\[SM = \frac{1}{2}\sqrt {4 \cdot {6^2} - {x^2}}  = \frac{1}{2}\sqrt {144 - {x^2}} \]

Diện tích xung quanh của hình chóp là: \[{S_{xq}} = \frac{{3x}}{2}.\frac{1}{2}\sqrt {144 - {x^2}}  = \frac{{3x}}{4}\sqrt {144 - {x^2}} \]

Vận dụng bất đẳng thức \[{a^2} + {b^2} \ge 2ab\]hay \[ab \le \frac{{{a^2} + {b^2}}}{2}\]ta được: \[x.\sqrt {144 - {x^2}}  \le \frac{{{x^2} + 144 - {x^2}}}{2} = 72\].

Do đó \[{S_{xq}} \le \frac{3}{4}.72 = 54\].

Dấu "=" xảy ra khi\[x = \sqrt {144 - {x^2}}  \Leftrightarrow {x^2} = 144 - {x^2} \Leftrightarrow {x^2} = 72 \Leftrightarrow x = 6\sqrt 2 \] .

Gọi thời gian vòi \[I\]chảy một mình đầy bề là \[x\] (giờ \[x > 5\])

Thời gian vòi \[II\] chảy một mình đầy vể là \[y\] (giờ, \[y > 5\])

Thời gian cả hai voi cùng chảy đầy bể là 5 giờ.

Trong 1 giờ, vòi \[I\] chảy được \(\frac{1}{x}\) bể; vòi \[II\] chảy được \(\frac{1}{y}\) bể; cả hai vòi cùng chảy được \(\frac{1}{5}\) bề.

Do đó ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\)                                                      \(\left( 1 \right)\)

Trong 3 giờ vòi \[I\] chảy được \(\frac{3}{x}\)bề; Trong 2 giờ vòi \[II\] chảy được \(\frac{2}{y}\) bề. Cả hai vòi chảy được \(\frac{2}{3}\) bề.

Do đó ta có phương trình: \(\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\)                                                      \(\left( 2 \right)\)

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{5}\\\frac{3}{x} + \frac{4}{y} = \frac{2}{3}\end{array} \right.\)

Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 7,5\\y = 15\end{array} \right.\) (thỏa mãn điều kiện).

Vậy:

Thời gian vòi \[I\] chảy một mình đầy bể là 7,5 giờ.

Thời gian vòi \[II\] chảy một mình đẩy bể là 15 giờ.