Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bắc Ninh

Đáp án đúng là: A

Căn bậc hai số học của 9 là \(3.\)

Hướng dẫn giải

Đáp án đúng là: B

Biểu thức \(\sqrt[3]{{x - 1}}\) có điều kiện xác định là \(x \in \mathbb{R}\).

Đáp án đúng là: B

Với \(a \ge 7,\,\,b \ge 8,\,\,c \ge 9,\) ta có:

\(a + b + c - 21 = 2\left( {\sqrt {a - 7} + \sqrt {b - 8} + \sqrt {c - 9} } \right)\)

\(a + b + c - 21 = 2\sqrt {a - 7} + 2\sqrt {b - 8} + 2\sqrt {c - 9} \)

\(\left( {a - 7 - 2\sqrt {a - 7} + 1} \right) + \left( {b - 8 - 2\sqrt {b - 8} + 1} \right) + \left( {c - 9 - 2\sqrt {c - 9} + 1} \right) = 0\)

\({\left( {\sqrt {a - 7} - 1} \right)^2} + {\left( {\sqrt {b - 8} - 1} \right)^2} + {\left( {\sqrt {c - 9} - 1} \right)^2} = 0\,\,\,\left( * \right)\)

Mà \({\left( {\sqrt {a - 7} - 1} \right)^2} \ge 0,\,\,{\left( {\sqrt {b - 8} - 1} \right)^2} \ge 0,\,\,{\left( {\sqrt {c - 9} - 1} \right)^2} \ge 0\) với mọi \(a \ge 7,\,\,b \ge 8,\,\,c \ge 9.\)

Khi đó từ $\left(*\right)$ suy ra ${\left(\sqrt{\mathrm{a}-7}-1\right)}^2=0,{\left(\sqrt{\mathrm{b}-8}-1\right)}^2=0,{\left(\sqrt{\mathrm{c}-9}-1\right)}^2=0$

Suy ra \[\sqrt {a - 7} - 1 = 0,\,\,\sqrt {b - 8} - 1 = 0,\,\,\sqrt {c - 9} - 1 = 0\]

Do đó \[a - 7 = 1,\,\,b - 8 = 1,\,\,c - 9 = 1\]

Nên \(a = 8,\,\,b = 9,\,\,c = 10\) (thỏa mãn).

Vậy \(S = a + 2b - c = 8 + 2 \cdot 9 - 10 = 16.\)

Đáp án đúng là: B

Xét hàm số \(y = 2{x^2}\):

⦁ Thay \(x = 2\) vào hàm số trên, ta được: \(y = 2 \cdot {2^2} = 8 \ne 1\) nên điểm \(\left( {2;1} \right)\) không thuộc đồ thị hàm số \(y = 2{x^2}.\)

⦁ Thay \(x = 1\) vào hàm số trên, ta được: \(y = 2 \cdot {1^2} = 2\) nên điểm \(\left( {1;2} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\) và điểm \(\left( {1;4} \right)\) không thuộc đồ thị hàm số \(y = 2{x^2}.\)

⦁ Thay \(x = 4\) vào hàm số trên, ta được: \(y = 2 \cdot {4^2} = 32 \ne 1\) nên điểm \(\left( {4;1} \right)\) không thuộc đồ thị hàm số \(y = 2{x^2}.\)

Vậy ta chọn phương án B.

Đáp án đúng là: D

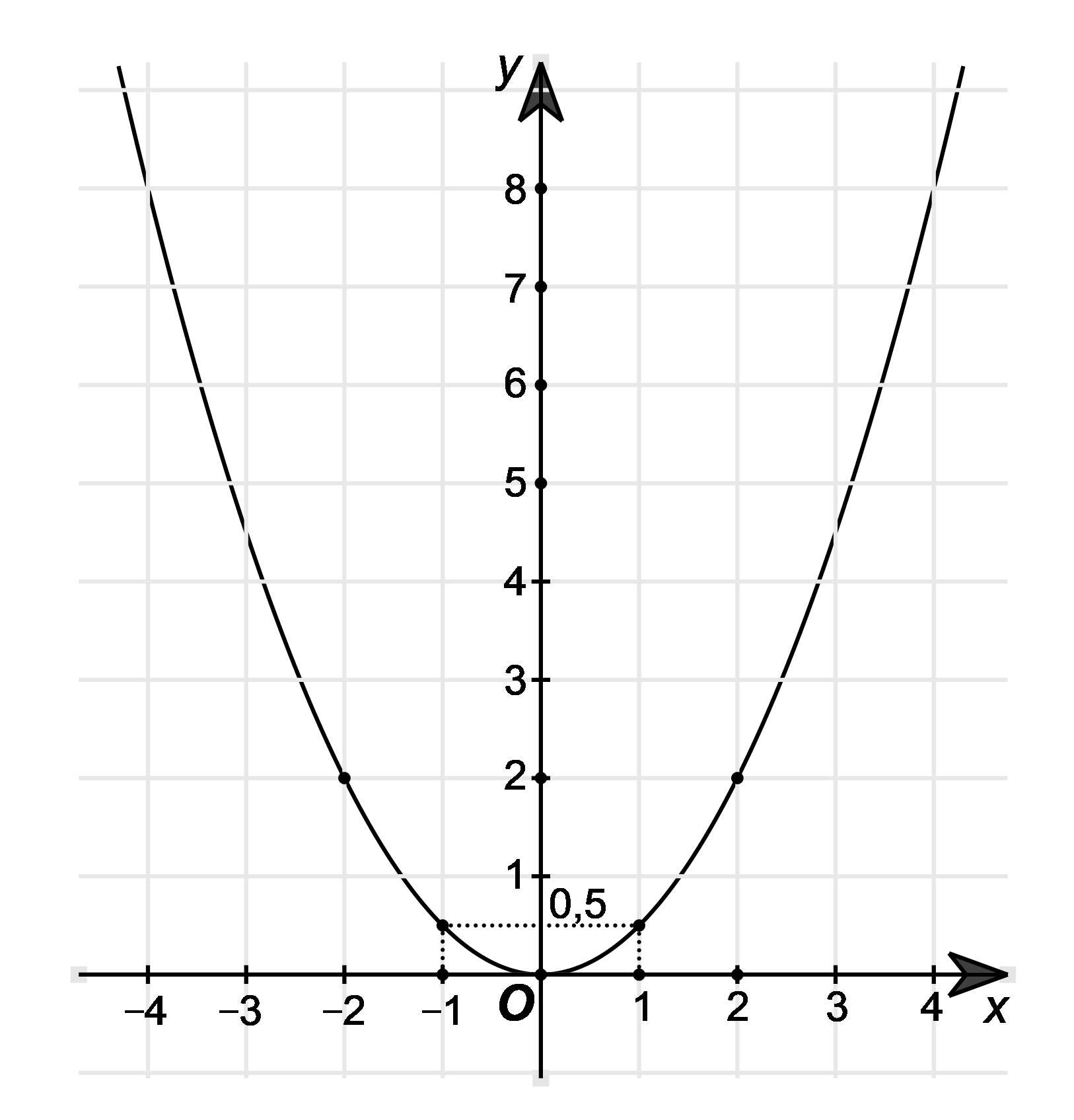
Quan sát hình vẽ, ta thấy parabol \(y = a{x^2}\) đi qua điểm \(\left( {1;\,\,0,5} \right)\) nên ta có:

\(0,5 = a \cdot {1^2},\) suy ra \(a = 0,5.\)

Khi đó, ta có hàm số \(y = 0,5{x^2}.\)

⦁ Thay \(x = - 1\) vào hàm số trên, ta được: \(y = 0,5 \cdot {\left( { - 1} \right)^2} = 0,5 \ne 1.\) Do đó parabol không đi qua điểm \(\left( { - 1;1} \right)\).

⦁ Thay \(x = 2\) vào hàm số trên, ta được: \(y = 0,5 \cdot {2^2} = 2.\) Do đó parabol đi qua điểm \(\left( {2;2} \right)\) và không đi qua điểm \(\left( {2;\,\, - 2} \right)\).

⦁ Thay \(x = 0,5\) vào hàm số trên, ta được: \(y = 0,5 \cdot {\left( {0,5} \right)^2} = 0,125 \ne 1.\) Do đó parabol không đi qua điểm \(\left( {0,5;1} \right)\).

Vậy ta chọn phương án D.

\(x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0\)

\(\left( {x + 1} \right)\left( {x - 2} \right) = 0\)

\(x + 1 = 0\) hoặc \(x - 2 = 0\)

\(x = - 1\) hoặc \(x = 2.\)

Hướng dẫn giải

Đáp án đúng là: C

Giải phương trình:

\(\left( {x + \frac{1}{3}} \right)\left( {x - 3} \right) = 0\)

\(x + \frac{1}{3} = 0\) hoặc \(x - 3 = 0\)

\(x = - \frac{1}{3}\) hoặc \(x = 3.\)

Vậy phương trình đã cho có nghiệm là \(x = - \frac{1}{3}\) và \(x = 3\).

Đáp án đúng là: B

Bất phương trình \(2x + 1 < 0\) là bất phương trình bậc nhất một ẩn có dạng \(ax + b < 0\) với \(a = 2,\,\,b = 1.\)