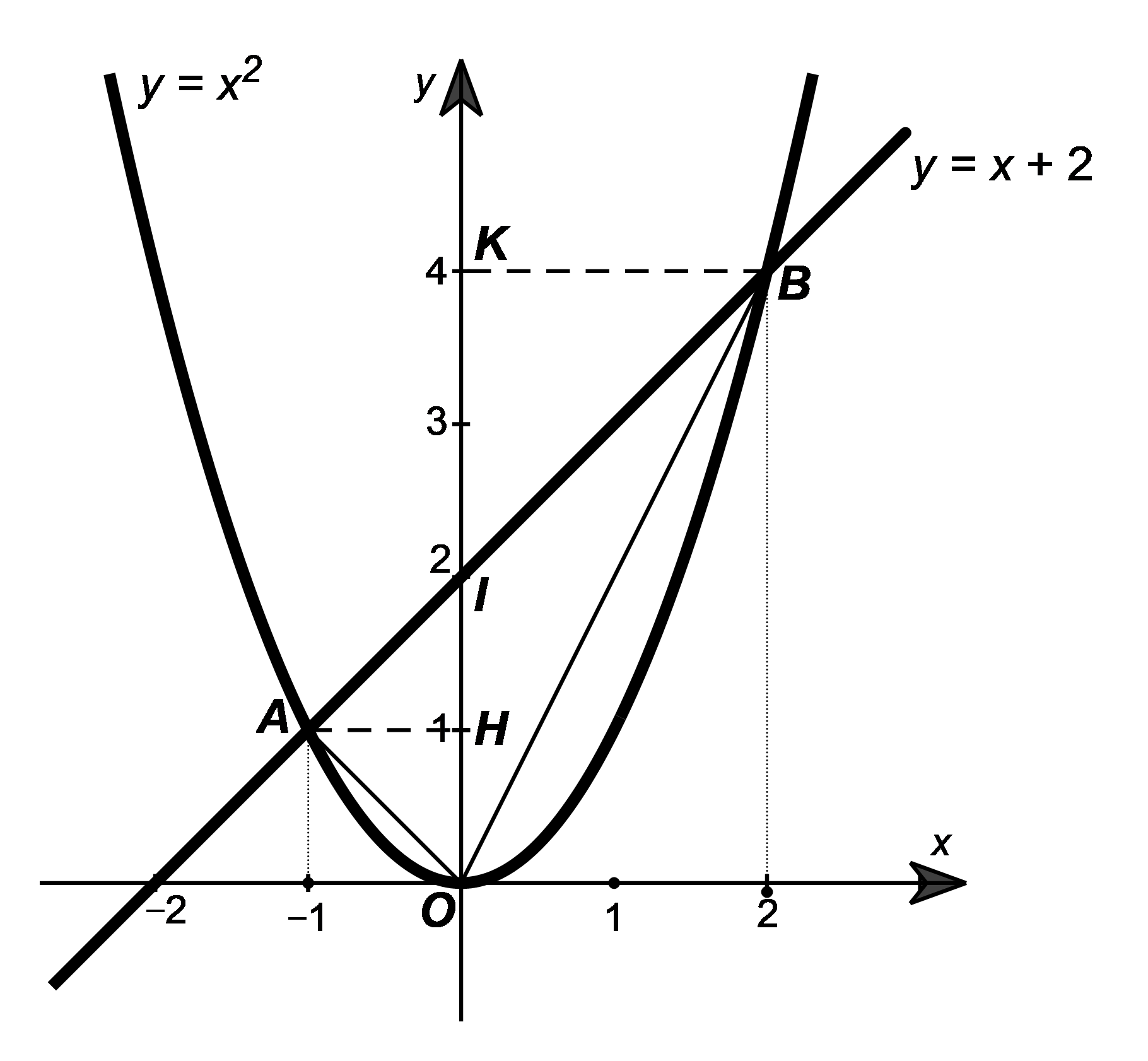Câu hỏi:
12/03/2025 195
Cho đường tròn \(\left( {O;\,\,3\;{\rm{cm}}} \right)\) và điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 5\;{\rm{cm}}{\rm{.}}\) Từ \(M\) kẻ đường thẳng \(d\) không đi qua tâm \(O\) cắt \(\left( O \right)\) tại hai điểm \(A,\,\,B.\) Tính tích \(MA \cdot MB\) ta được kết quả là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
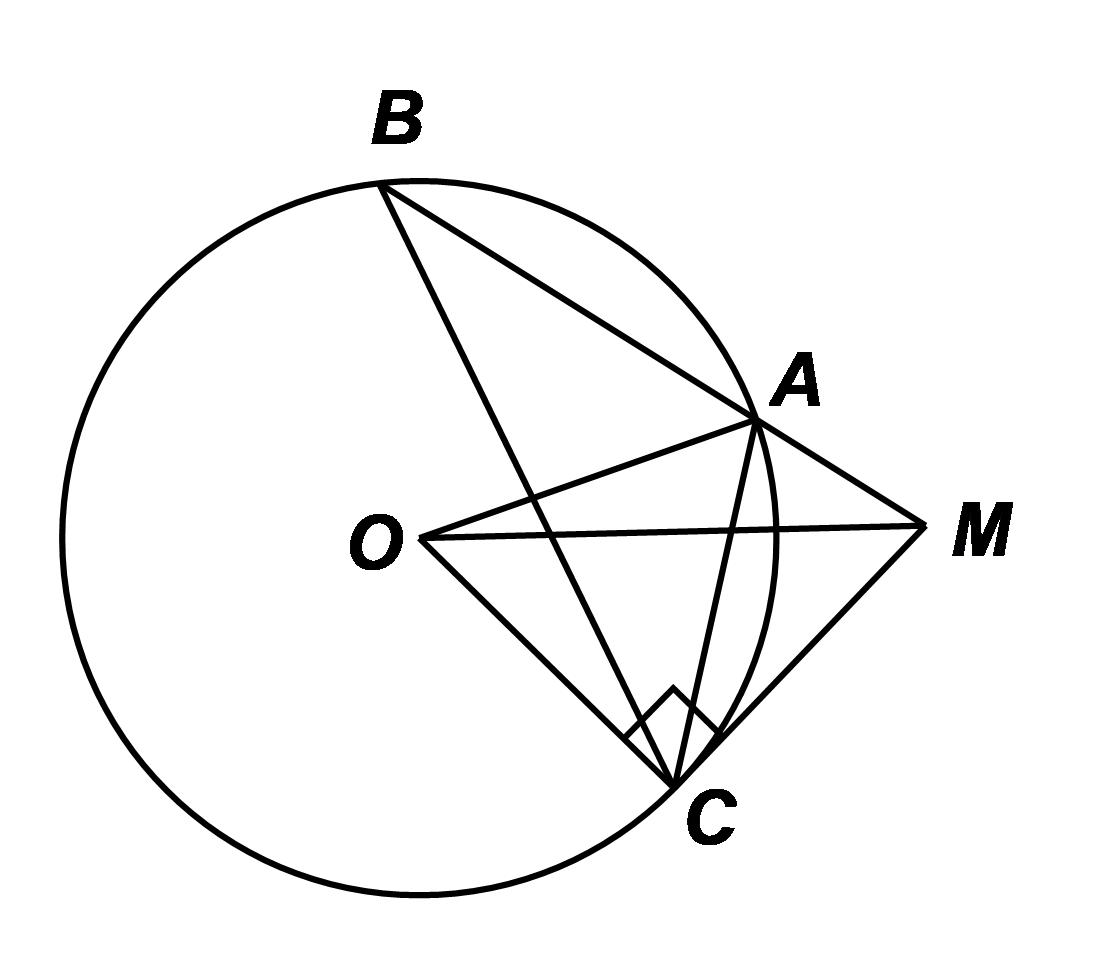
Giả sử \(MC\) là tiếp tuyến của đường tròn \(\left( O \right)\) \((C\) là tiếp điểm).
Xét \(\Delta OAC\) cân tại \(O\) (do \(OA = OC)\) nên
\(\widehat {OCA} = \widehat {OAC} = \frac{{180^\circ - \widehat {AOC}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOC}.\)Mà \(\widehat {ABC} = \frac{1}{2}\widehat {AOC}\) (do \(\widehat {ABC},\,\,\widehat {AOC}\) lần lượt là góc nội tiếp, góc ở tâm cùng chắn cung \(AC\) của đường tròn \(\left( O \right)).\)
Suy ra \(\widehat {OCA} = 90^\circ - \widehat {ABC}\) hay \(\widehat {ABC} = 90^\circ - \widehat {OCA}.\)
Lại có \(\widehat {OCA} + \widehat {ACM} = 90^\circ \) nên \(\widehat {ACM} = 90^\circ - \widehat {OCA}.\) Như vậy, \(\widehat {ABC} = \widehat {ACM}.\)
Xét \(\Delta MAC\) và \(\Delta MCB\) có: \(\widehat {BMC}\) là góc chung và \(\widehat {MCA} = \widehat {MBC}.\)
Do đó (g.g). Suy ra \(\frac{{MA}}{{MC}} = \frac{{MC}}{{MB}}\) nên \(MA \cdot MB = M{C^2}.\)
Xét \(\Delta OMC\) vuông tại \(C,\) theo định lí Pythagore, ta có: \(O{M^2} = O{C^2} + M{C^2}\)
Suy ra \(M{C^2} = O{M^2} - O{C^2} = {5^2} - {3^2} = 16.\)
Vậy \(MA \cdot MB = M{C^2} = 16.\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Hướng dẫn giải Đáp án đúng là: D Phương trình hoành độ giao điểm của parabol \(y = {x^2}\) và đường thẳng \(y = x + 2\) là: \({x^2} = x + 2\) \({x^2} - x - 2 = 0\) \(\left( {{x^2} + x} \right) - \left( {2x + 2} \right) = 0\) |
|
\(x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0\)
\(\left( {x + 1} \right)\left( {x - 2} \right) = 0\)
\(x + 1 = 0\) hoặc \(x - 2 = 0\)
\(x = - 1\) hoặc \(x = 2.\)
Thay \(x = - 1\) vào hàm số \(y = {x^2},\) ta được \(y = {\left( { - 1} \right)^2} = 1.\)
Thay \(x = 2\) vào hàm số \(y = {x^2},\) ta được \(y = {2^2} = 4.\)
Như vậy, đường thẳng \(y = x + 2\) cắt parabol \(y = {x^2}\) tại hai điểm \(A\left( { - 1;\,\,1} \right)\) và \(B\left( {2;\,\,4} \right).\)
Gọi giao điểm của đường thẳng \(y = x + 2\) với trục tung là \(I\left( {0;\,\,2} \right).\) Suy ra \(OI = \left| 2 \right| = 2.\)
Gọi hình chiếu của \(A\left( { - 1;\,\,1} \right),\,\,B\left( {2;\,\,4} \right)\) lên trục tung lần lượt là \(H\left( {0;\,\,1} \right)\) và \(K\left( {0;\,\,4} \right).\)
Suy ra \(AH = \left| { - 1} \right| = 1;\,\,BK = \left| 2 \right| = 2.\)
Ta có: \({S_{\Delta OAI}} = \frac{1}{2} \cdot AH \cdot OI = \frac{1}{2} \cdot 1 \cdot 2 = 1\) (đơn vị diện tích);
\[{S_{\Delta OBI}} = \frac{1}{2} \cdot BK \cdot OI = \frac{1}{2} \cdot 2 \cdot 2 = 2\] (đơn vị diện tích).
Vậy diện tích của tam giác \(OAB\) là: \({S_{\Delta OAB}} = {S_{\Delta OAI}} + {S_{\Delta OBI}} = 1 + 2 = 3\) (đơn vị diện tích).
Lời giải
Đáp án đúng là: D
Bán kính đường tròn ngoại tiếp tam giác đều cạnh 6 cm là \(\frac{{6 \cdot \sqrt 3 }}{3} = 2\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước