Câu hỏi:
12/03/2025 215
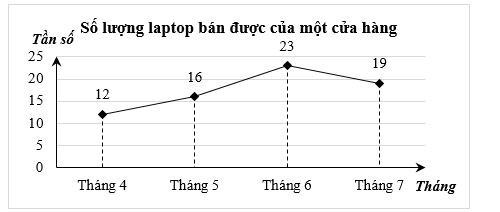
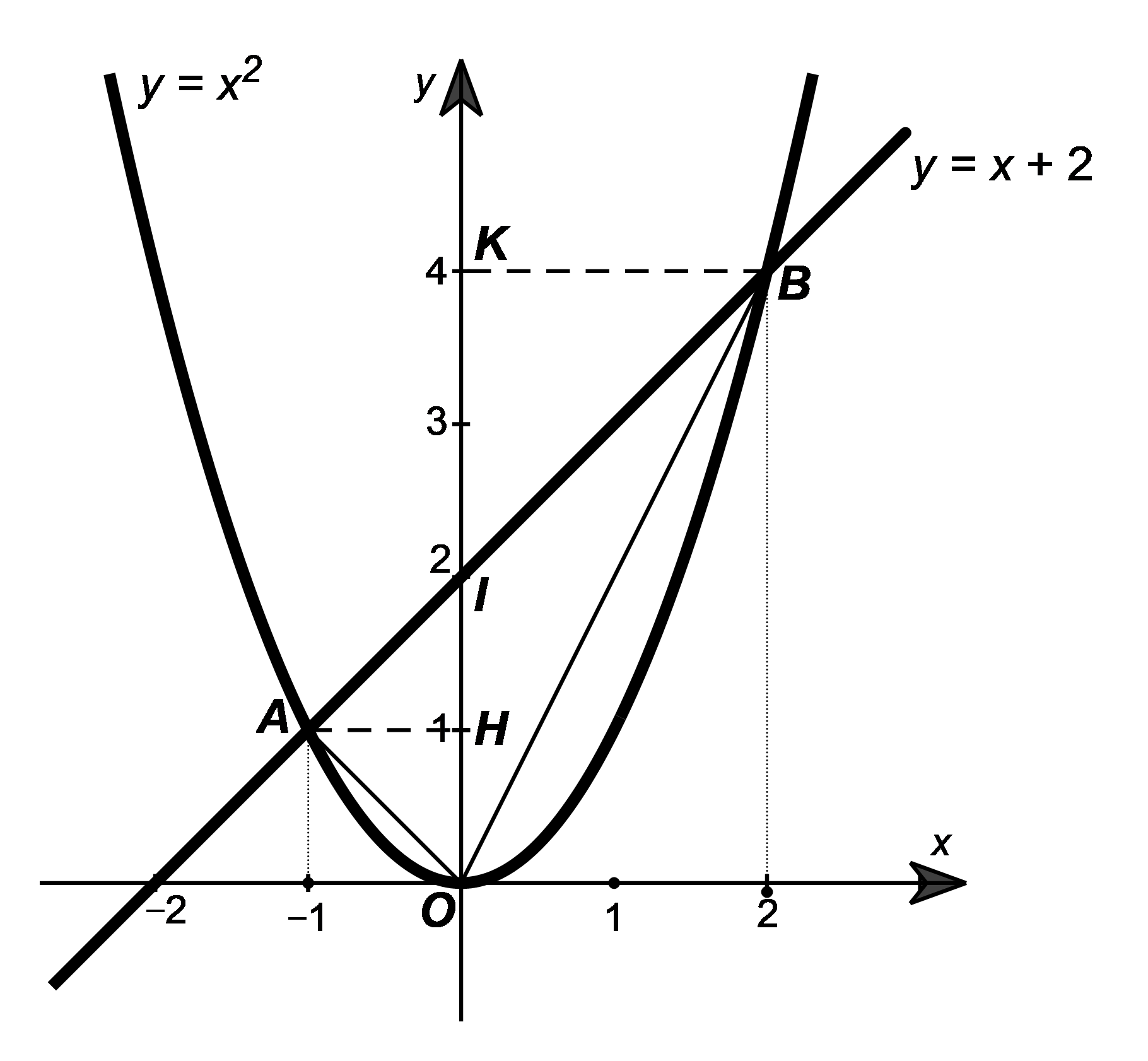Biểu đồ tần số ở hình dưới đây biểu diễn số lượng laptop bán được của một cửa hàng trong bốn tháng 4, 5, 6, 7.
Nếu mỗi laptop bán ra cửa hàng được lãi 800 000 đồng thì sau bốn tháng 4, 5, 6, 7 cửa hàng thu được số tiền lãi là
Biểu đồ tần số ở hình dưới đây biểu diễn số lượng laptop bán được của một cửa hàng trong bốn tháng 4, 5, 6, 7.
Nếu mỗi laptop bán ra cửa hàng được lãi 800 000 đồng thì sau bốn tháng 4, 5, 6, 7 cửa hàng thu được số tiền lãi là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Cửa hàng bán được số chiếc laptop trong bốn tháng 4, 5, 6, 7 là: \(12 + 16 + 23 + 19 = 70\) (chiếc).
Số tiền lãi cửa hàng thu được là: \(70 \cdot 800\,\,000 = 56\,\,000\,\,000\) (đồng).
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Hướng dẫn giải Đáp án đúng là: D Phương trình hoành độ giao điểm của parabol \(y = {x^2}\) và đường thẳng \(y = x + 2\) là: \({x^2} = x + 2\) \({x^2} - x - 2 = 0\) \(\left( {{x^2} + x} \right) - \left( {2x + 2} \right) = 0\) |
|
\(x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0\)
\(\left( {x + 1} \right)\left( {x - 2} \right) = 0\)
\(x + 1 = 0\) hoặc \(x - 2 = 0\)
\(x = - 1\) hoặc \(x = 2.\)
Thay \(x = - 1\) vào hàm số \(y = {x^2},\) ta được \(y = {\left( { - 1} \right)^2} = 1.\)
Thay \(x = 2\) vào hàm số \(y = {x^2},\) ta được \(y = {2^2} = 4.\)
Như vậy, đường thẳng \(y = x + 2\) cắt parabol \(y = {x^2}\) tại hai điểm \(A\left( { - 1;\,\,1} \right)\) và \(B\left( {2;\,\,4} \right).\)
Gọi giao điểm của đường thẳng \(y = x + 2\) với trục tung là \(I\left( {0;\,\,2} \right).\) Suy ra \(OI = \left| 2 \right| = 2.\)
Gọi hình chiếu của \(A\left( { - 1;\,\,1} \right),\,\,B\left( {2;\,\,4} \right)\) lên trục tung lần lượt là \(H\left( {0;\,\,1} \right)\) và \(K\left( {0;\,\,4} \right).\)
Suy ra \(AH = \left| { - 1} \right| = 1;\,\,BK = \left| 2 \right| = 2.\)
Ta có: \({S_{\Delta OAI}} = \frac{1}{2} \cdot AH \cdot OI = \frac{1}{2} \cdot 1 \cdot 2 = 1\) (đơn vị diện tích);
\[{S_{\Delta OBI}} = \frac{1}{2} \cdot BK \cdot OI = \frac{1}{2} \cdot 2 \cdot 2 = 2\] (đơn vị diện tích).
Vậy diện tích của tam giác \(OAB\) là: \({S_{\Delta OAB}} = {S_{\Delta OAI}} + {S_{\Delta OBI}} = 1 + 2 = 3\) (đơn vị diện tích).
Lời giải
Đáp án đúng là: D
Bán kính đường tròn ngoại tiếp tam giác đều cạnh 6 cm là \(\frac{{6 \cdot \sqrt 3 }}{3} = 2\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_TP Phú Thọ
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa