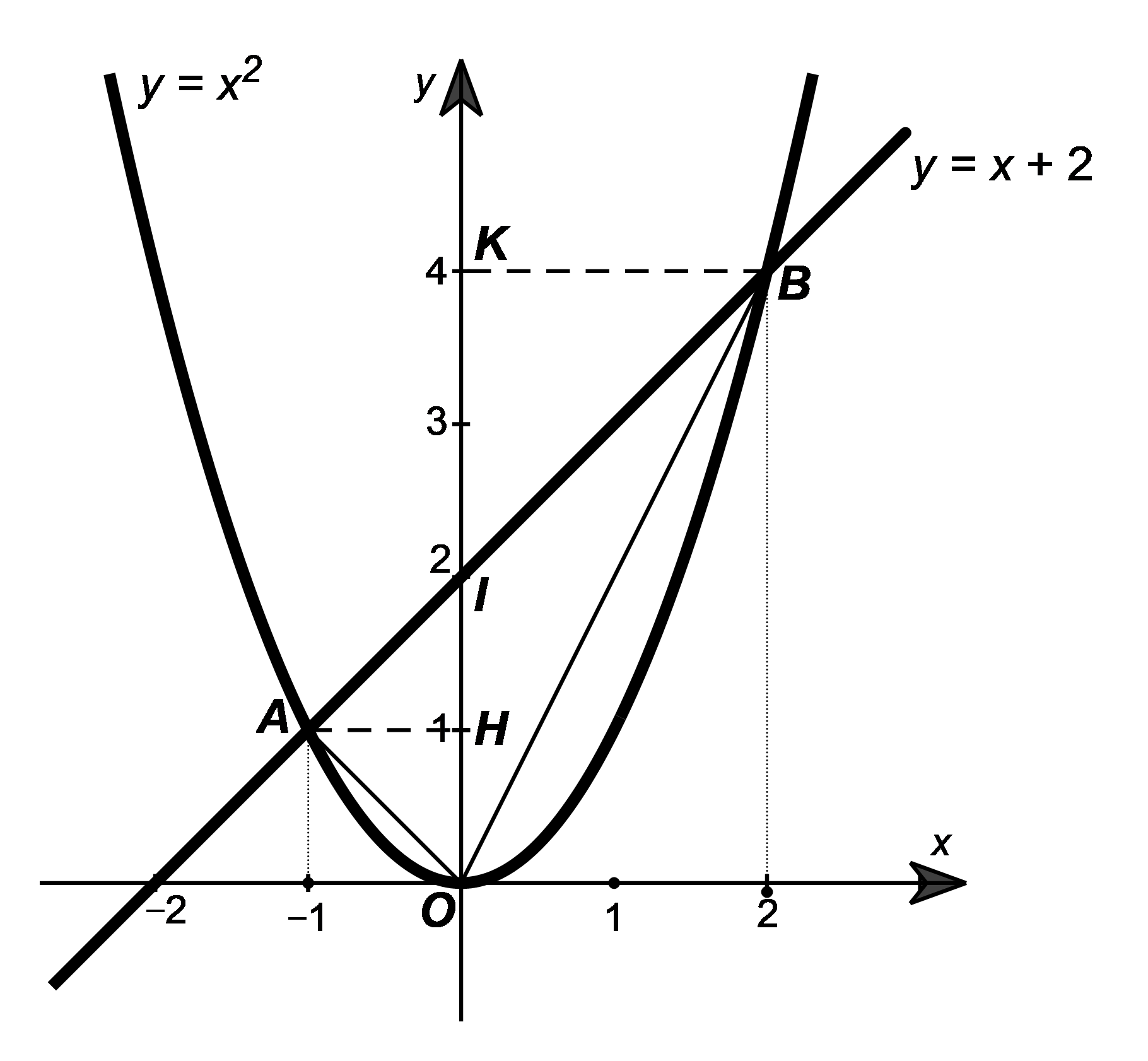Câu hỏi:
12/03/2025 368
Câu 40-41: (1,0 điểm)
1) Cho \(a,\,\,b,\,\,c\) là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức\(P = \frac{{3\left( {b + c} \right)}}{{2a}} + \frac{{4a + 3c}}{{3b}} + \frac{{12\left( {b - c} \right)}}{{2a + 3c}}.\)
Câu 40-41: (1,0 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
⦁ Chứng minh bổ đề 1: Với \(x > 0,\,\,y > 0\) ta luôn có \(\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}.\)
Thật vậy, với \(x > 0,\,\,y > 0\) ta luôn có:
\({\left( {x - y} \right)^2} \ge 0\)
\({x^2} - 2xy + {y^2} \ge 0\)
\({x^2} + 2xy + {y^2} \ge 4xy\)
\({\left( {x + y} \right)^2} \ge 4xy\)
\(\frac{{{{\left( {x + y} \right)}^2}}}{{xy\left( {x + y} \right)}} \ge \frac{{4xy}}{{xy\left( {x + y} \right)}}\)
\(\frac{{x + y}}{{xy}} \ge \frac{4}{{x + y}}\)
\(\frac{1}{x} + \frac{1}{y} \ge \frac{4}{{x + y}}\).
Dấu “=” xảy ra khi và chỉ khi \(x = y.\) Bất đẳng thức được chứng minh.
Chứng minh bổ đề 2: Với \(x > 0,\,\,y > 0\) ta luôn có \(\frac{x}{y} + \frac{y}{x} \ge 2.\)
Thật vậy, với \(x > 0,\,\,y > 0\) ta luôn có:
\({\left( {x - y} \right)^2} \ge 0\)
\({x^2} - 2xy + {y^2} \ge 0\)
\({x^2} + {y^2} \ge 2xy\)
\(\frac{{{x^2} + {y^2}}}{{xy}} \ge \frac{{2xy}}{{xy}}\)
\(\frac{x}{y} + \frac{y}{x} \ge 2.\)
Dấu “=” xảy ra khi và chỉ khi \(x = y.\) Bất đẳng thức được chứng minh.
⦁ Với \(a,\,\,b,\,\,c\) là các số thực dương, ta có:
\(P = \frac{{3\left( {b + c} \right)}}{{2a}} + \frac{{4a + 3c}}{{3b}} + \frac{{12\left( {b - c} \right)}}{{2a + 3c}}\)
\( = \frac{{3b}}{{2a}} + \frac{{3c}}{{2a}} + \frac{{4a}}{{3b}} + \frac{{3c}}{{3b}} + \frac{{12\left( {b - c} \right)}}{{2a + 3c}} + 4 - 4\)
\( = \left( {\frac{{3b}}{{2a}} + \frac{{2a}}{{3b}}} \right) + \left( {\frac{{2a}}{{3b}} + 1} \right) + \left( {\frac{{3c}}{{2a}} + \frac{{3c}}{{3b}}} \right) + \frac{{12b - 12c + 8a + 12c}}{{2a + 3c}} - 5\)
\( = \left( {\frac{{3b}}{{2a}} + \frac{{2a}}{{3b}}} \right) + \left( {\frac{{2a}}{{3b}} + \frac{{2a}}{{2a}}} \right) + \left( {\frac{{3c}}{{2a}} + \frac{{3c}}{{3b}}} \right) + \frac{{4\left( {3b + 2a} \right)}}{{2a + 3c}} - 5\)
\( = \left( {\frac{{3b}}{{2a}} + \frac{{2a}}{{3b}}} \right) + 2a\left( {\frac{1}{{3b}} + \frac{1}{{2a}}} \right) + 3c\left( {\frac{1}{{2a}} + \frac{1}{{3b}}} \right) + \frac{{4\left( {3b + 2a} \right)}}{{2a + 3c}} - 5.\)
⦁ Áp dụng bất đẳng thức Cauchy, ta có: \(\frac{{3b}}{{2a}} + \frac{{2a}}{{3b}} \ge 2\sqrt {\frac{{3b}}{{2a}} \cdot \frac{{2a}}{{3b}}} = 2.\)
Áp dụng bất đẳng thức bổ đề 1 đã chứng minh ở trên, ta có:
\[2a\left( {\frac{1}{{3b}} + \frac{1}{{2a}}} \right) \ge \frac{{2a \cdot 4}}{{2a + 3b}}\] và \[3c\left( {\frac{1}{{2a}} + \frac{1}{{3b}}} \right) \ge \frac{{3c \cdot 4}}{{2a + 3b}}.\]
Do đó \(P = \left( {\frac{{3b}}{{2a}} + \frac{{2a}}{{3b}}} \right) + 2a\left( {\frac{1}{{3b}} + \frac{1}{{2a}}} \right) + 3c\left( {\frac{1}{{2a}} + \frac{1}{{3b}}} \right) + \frac{{4\left( {3b + 2a} \right)}}{{2a + 3c}} - 5\)
\[ \ge 2 + \frac{{2a \cdot 4}}{{2a + 3b}} + \frac{{3c \cdot 4}}{{2a + 3b}} + \frac{{4\left( {3b + 2a} \right)}}{{2a + 3c}} - 5\]
\[ \ge 2 + 4\left( {\frac{{2a + 3c}}{{2a + 3b}} + \frac{{2a + 3b}}{{2a + 3c}}} \right) - 5\]
\[ \ge 2 + 4 \cdot 2 - 5\] (áp dụng bất đẳng thức bổ đề 2 đã chứng minh)
\[ = 5.\]
Như vậy, \(P \ge 5.\) Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}\frac{{3b}}{{2a}} = \frac{{2a}}{{3b}}\\\frac{1}{{3b}} = \frac{1}{{2a}}\\\frac{1}{{2a}} = \frac{1}{{3b}}\\\frac{{2a + 3c}}{{2a + 3b}} = \frac{{2a + 3b}}{{2a + 3c}}\end{array} \right.\) tức là \(2a = 3b = 3c.\)
Vậy \(P\) đạt giá trị nhỏ nhất bằng 5 khi \(2a = 3b = 3c.\)
Câu hỏi cùng đoạn
Câu 2:
2) Người ta vẽ bản quy hoạch của một khu dân cư được bao quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là \(900\;{\rm{m}},\,\,1200\;{\rm{m}}\) và 1500 m như hình vẽ. Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng bằng bao nhiêu?
Lời giải của GV VietJack
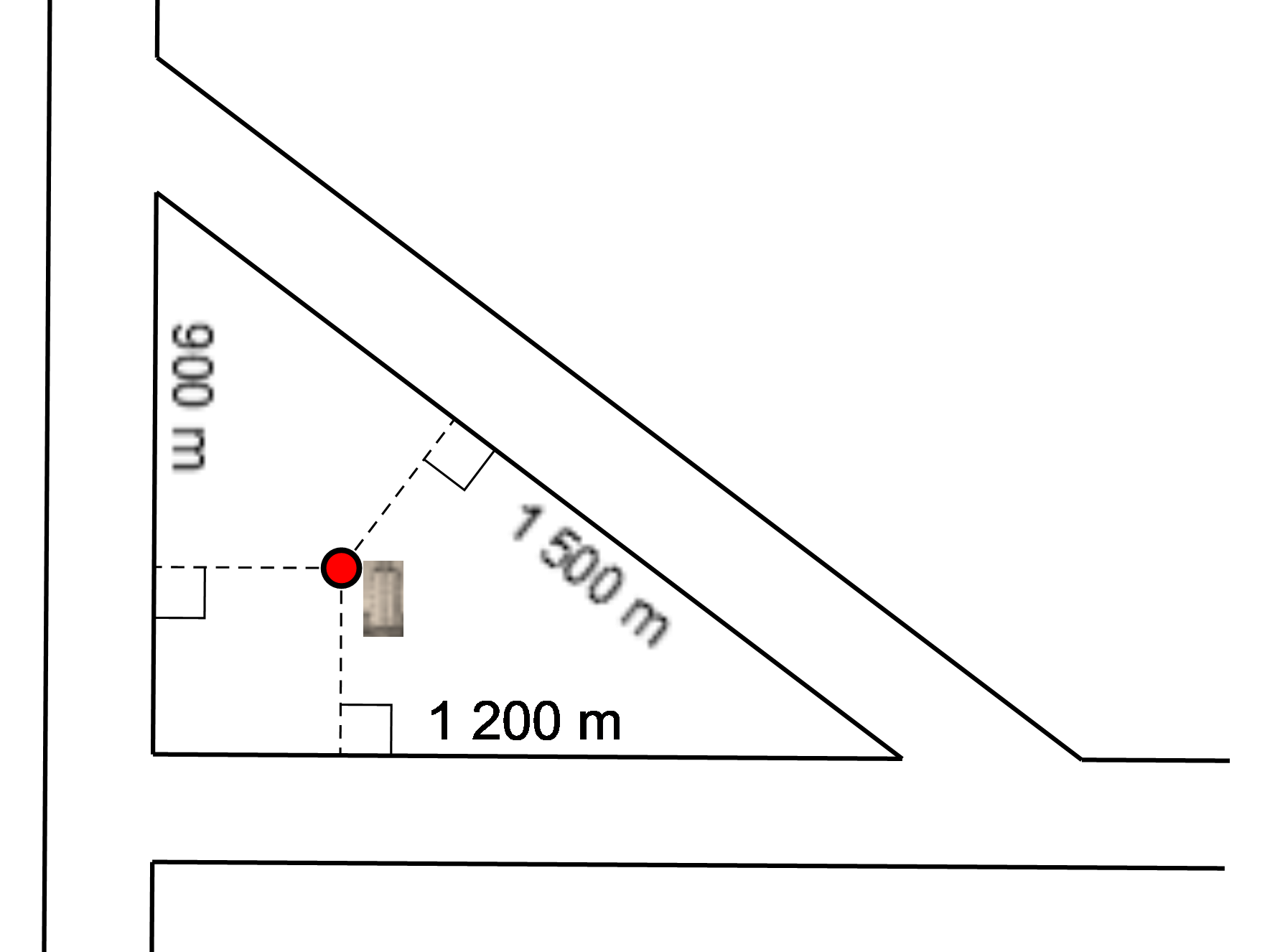
Gọi \[A,{\rm{ }}B,{\rm{ }}C\] là ba đỉnh của khu dân cư sao cho \[AB = 900\] m, \[AC = 1{\rm{ }}200\] m và \[BC = 1{\rm{ }}500\] m.
Xét \(\Delta ABC\) có:
⦁ \[A{B^2} + A{C^2} = {900^2} + 1{\rm{ }}{200^2} = 2{\rm{ }}250{\rm{ }}000;\]
⦁ \[B{C^2} = 1{\rm{ }}{500^2} = 2{\rm{ }}250{\rm{ }}000.\]
Do đó \[A{B^2} + A{C^2} = B{C^2},\] nên theo định lí Pythagore đảo ta có \(\Delta ABC\) vuông tại \[A.\]Gọi \[O\] là vị trí xây dựng khách sạn; \[H,{\rm{ }}I,{\rm{ }}K\] lần lượt là chân đường vuông góc kẻ từ \[O\] đến \[AB,{\rm{ }}BC,{\rm{ }}CA.\]
Vì vị trí xây dựng khách sạn cách đều cả ba con đường nên \[OH = OI = OK.\]
Mặt khác, \({S_{OAB}} = \frac{1}{2} \cdot OH \cdot AB;\) \({S_{OBC}} = \frac{1}{2} \cdot OI \cdot BC;\) \({S_{OCA}} = \frac{1}{2} \cdot OK \cdot CA.\)
Mà \({S_{ABC}} = {S_{OAB}} + {S_{OBC}} + {S_{OCA}}\)
Suy ra \[{S_{ABC}} = \frac{1}{2} \cdot OH \cdot AB + \frac{1}{2} \cdot OI \cdot BC + \frac{1}{2} \cdot OK \cdot CA\]
Do đó \[{S_{ABC}} = \frac{1}{2} \cdot OH \cdot \left( {AB + BC + CA} \right)\]
Nên \(OH = \frac{{2{S_{ABC}}}}{{AB + BC + CA}}{\rm{.}}\)
Chu vi của phần đất giới hạn bởi tam giác \[ABC\] là:
\[AB + BC + CA = 900 + 1{\rm{ }}500 + 1{\rm{ }}200{\rm{ }} = 3{\rm{ }}600\] (m).
Diện tích của phần đất giới hạn bởi tam giác \[ABC\] là:
\({S_{ABC}} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 900 \cdot 1\,\,200 = 540\,\,000{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Do đó \(OH = \frac{{2{S_{ABC}}}}{{AB + BC + CA}} = \frac{{2 \cdot 540\,\,000}}{{3\,\,600}} = 300{\rm{\;(m)}}{\rm{.}}\)
Vậy khách sạn sẽ cách mỗi con đường một khoảng là 300 mét.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giao điểm của parabol \(y = {x^2}\) và đường thẳng \(y = x + 2\) cùng với gốc tọa độ tạo thành tam giác có diện tích bằng
Xem đáp án »
12/03/2025
1,754
Câu 4:
Hình nón có chiều cao bằng 12 cm, bán kính đáy bằng 9 cm thì diện tích xung quanh là
Xem đáp án »
12/03/2025
611
Câu 5:
Bạn Bắc gieo một con xúc xắc 50 lần cho kết quả như sau:
Số chấm xuất hiện
1
2
3
4
5
6
Tần số
8
7
10
8
6
11
Tần số xuất hiện mặt 3 chấm là
Bạn Bắc gieo một con xúc xắc 50 lần cho kết quả như sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Tần số |
8 |
7 |
10 |
8 |
6 |
11 |
Xem đáp án »
12/03/2025
523
Câu 6:
Bạn Ninh gieo một con xúc xắc liên tiếp hai lần. Số phần tử của không gian mẫu là
Xem đáp án »
12/03/2025
512
Câu 7:
Trong các phương trình bậc hai sau phương trình nào có tổng hai nghiệm bằng 3?
Xem đáp án »
12/03/2025
511
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận