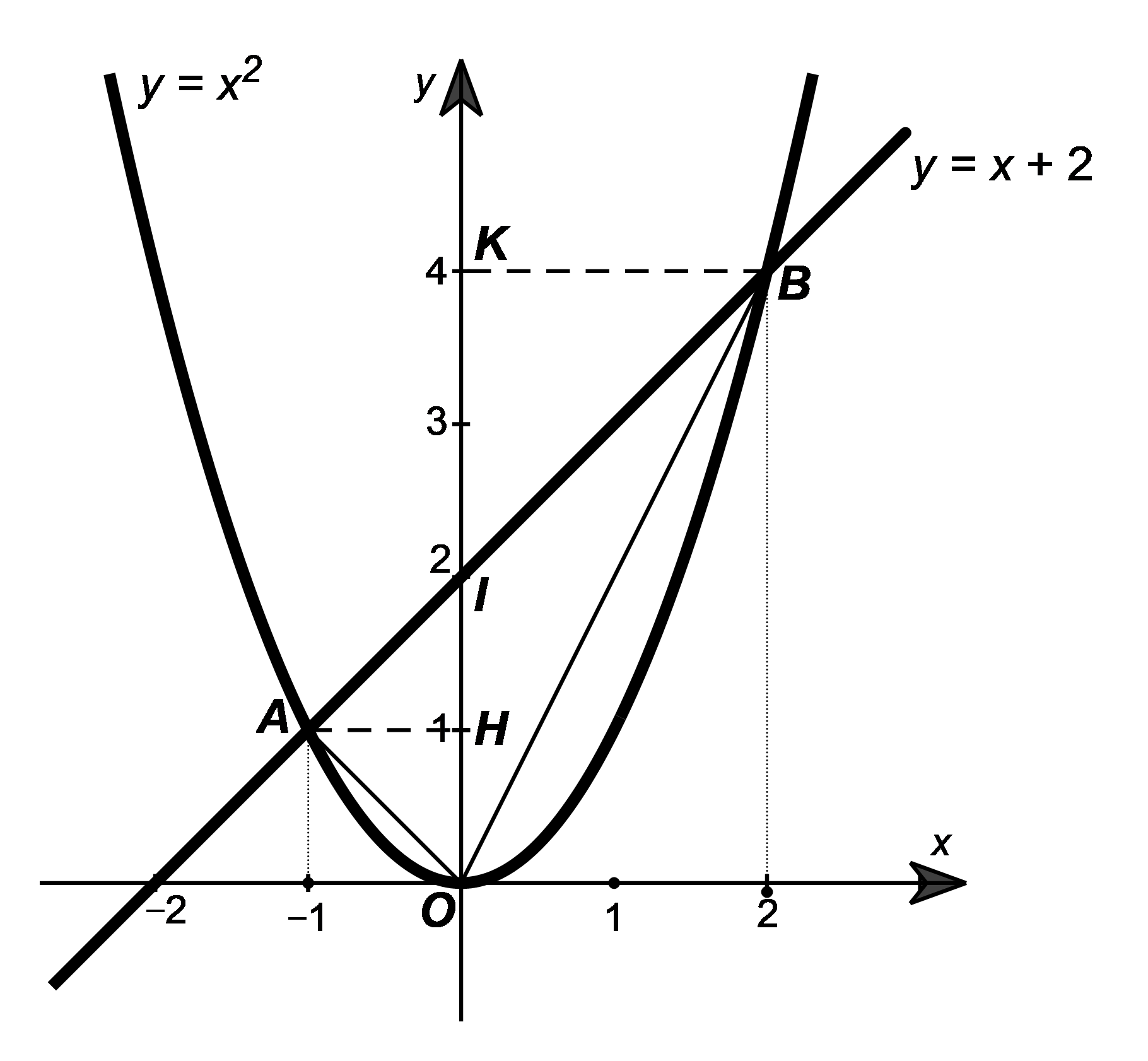Câu hỏi:
12/03/2025 303
Câu 37-39: (2,0 điểm) Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\) đường kính \(AD.\) Gọi \(H\) là giao điểm của \(AC\) và \(BD,\) kẻ \(HK \bot AD\,\,\left( {K \in AD} \right).\)
1) Chứng minh tứ giác \(CDKH\) nội tiếp.
Câu 37-39: (2,0 điểm) Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\) đường kính \(AD.\) Gọi \(H\) là giao điểm của \(AC\) và \(BD,\) kẻ \(HK \bot AD\,\,\left( {K \in AD} \right).\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét đường tròn \(\left( O \right)\) đường kính \(AD\) có \[\widehat {ACD} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn) hay \(\Delta HCD\) vuông tại \(C.\)
Suy ra ba điểm \(H,\,\,C,\,\,D\) cùng nằm trên đường tròn đường kính \(HD.\)
Ta có \(\widehat {HKD} = 90^\circ \) nên ba điểm \(H,\,\,K,\,\,D\) cùng nằm trên đường tròn đường kính \(HD.\)
Do đó, bốn điểm \(C,\,\,D,\,\,K,\,\,H\) cùng nằm trên đường tròn đường kính \(HD.\)
Vậy tứ giác \(CDKH\) nội tiếp đường tròn đường kính \(HD.\)Câu hỏi cùng đoạn
Câu 2:
2) Gọi \(M\) là giao điểm của \(AB\) và \[CD.\] Chứng minh ba điểm \(M,H,K\) thẳng hàng.
Lời giải của GV VietJack
Vì \(\widehat {HCD} = 90^\circ \) nên \(\widehat {HCM} = 90^\circ ,\) suy ra ba điểm \(H,\,\,C,\,\,M\) cùng nằm trên đường tròn đường kính \(HM.\)
Tương tự, ta có ba điểm \(H,\,\,B,\,\,M\) cùng nằm trên đường tròn đường kính \(HM.\)
Do đó, bốn điểm \(H,\,\,B,\,\,M,\,\,C\) cùng nằm trên đường tròn đường kính \(HM.\)
Như vậy, tứ giác \(HBMC\) nội tiếp đường tròn đường kính \(HM.\)
Suy ra \(\widehat {MHC} = \widehat {MBC}\) (hai góc nội tiếp cùng chắn cung \(MC).\) (1)
Do tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \[\widehat {CBA} + \widehat {ADC} = 180^\circ \] (tổng hai góc đối nhau)
Tứ giác \(CDKH\) nội tiếp đường tròn đường kính \(HD\) nên \(\widehat {CHK} + \widehat {KDC} = 180^\circ \) (tổng hai góc đối nhau) hay \[\widehat {CHK} + \widehat {ADC} = 180^\circ \].
Suy ra \[\widehat {CBA} = \widehat {CHK}.\]
Lại có \[\widehat {MBC} + \widehat {CBA} = 180^\circ \] (hai góc kề bù) nên \[\widehat {MBC} + \widehat {CHK} = 180^\circ \] (2)
Từ (1) và (2) suy ra \[\widehat {MHC} + \widehat {CHK} = 180^\circ \] hay \(\widehat {MHK} = 180^\circ .\)
Do đó ba điểm \(M,\,\,H,\,\,K\) thẳng hàng.
Câu 3:
3) Gọi \(N\) là giao điểm của \(CK\) và \(BD.\) Chứng minh rằng \(BD \cdot HN = DN \cdot HB.\)
Lời giải của GV VietJack
⦁ Tứ giác \(CDKH\) nội tiếp nên \(\widehat {HCK} = \widehat {HDK}\) (hai góc nội tiếp cùng chắn cung \(HK)\)
Tứ giác \(HBMC\) nội tiếp nên \(\widehat {HCB} = \widehat {HMB}\) (hai góc nội tiếp cùng chắn cung \(BH)\)
Mà \(\widehat {BDA} = \widehat {KMA}\) (cùng phụ với \(\widehat {MAD})\) hay \(\widehat {HDK} = \widehat {HMB}\) nên \(\widehat {HCK} = \widehat {HCB}\)
Suy ra \(CH\) là tia phân giác của \(\widehat {BCK}.\)
Xét \(\Delta BCN\) có \(CH\) là tia phân giác của \(\widehat {BCN}\) nên \(\frac{{HN}}{{HB}} = \frac{{CN}}{{CB}}\) (tính chất tia phân giác). (5)
⦁ Kẻ đường thẳng song song với \(CK,\) cắt \(MD\) tại \(P.\)
Xét \(\Delta BDP\) có \(BP\,{\rm{//}}\,CN\) nên \(\frac{{CN}}{{PB}} = \frac{{DN}}{{DB}}\) (hệ quả định lí Thalès). (3)
Ta có \(\widehat {HCK} + \widehat {KCD} = 90^\circ \) và \(\widehat {HCB} + \widehat {BCP} = 90^\circ \)
Mà \(\widehat {HCK} = \widehat {HCB}\) (chứng minh trên) nên \(\widehat {KCD} = \widehat {BCP}.\)
Do \(BP\,{\rm{//}}\,CK\) nên \(\widehat {BPC} = \widehat {KCD}\) (hai góc đồng vị).
Suy ra \(\widehat {BCP} = \widehat {BPC}\) nên \(\Delta BCP\) cân tại \(B.\) Do đó \[BC = BP.\] (4)
Từ (3) và (4) suy ra \(\frac{{CN}}{{BC}} = \frac{{DN}}{{DB}}\) (6)
⦁ Từ (5) và (6) suy ra \(\frac{{HN}}{{HB}} = \frac{{DN}}{{DB}}\) hay \(BD \cdot HN = DN \cdot HB.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giao điểm của parabol \(y = {x^2}\) và đường thẳng \(y = x + 2\) cùng với gốc tọa độ tạo thành tam giác có diện tích bằng
Xem đáp án »
12/03/2025
1,757
Câu 4:
Hình nón có chiều cao bằng 12 cm, bán kính đáy bằng 9 cm thì diện tích xung quanh là
Xem đáp án »
12/03/2025
612
Câu 5:
Bạn Bắc gieo một con xúc xắc 50 lần cho kết quả như sau:
Số chấm xuất hiện
1
2
3
4
5
6
Tần số
8
7
10
8
6
11
Tần số xuất hiện mặt 3 chấm là
Bạn Bắc gieo một con xúc xắc 50 lần cho kết quả như sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Tần số |
8 |
7 |
10 |
8 |
6 |
11 |
Xem đáp án »
12/03/2025
523
Câu 6:
Trong các phương trình bậc hai sau phương trình nào có tổng hai nghiệm bằng 3?
Xem đáp án »
12/03/2025
517
Câu 7:
Bạn Ninh gieo một con xúc xắc liên tiếp hai lần. Số phần tử của không gian mẫu là
Xem đáp án »
12/03/2025
512
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận