Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 26

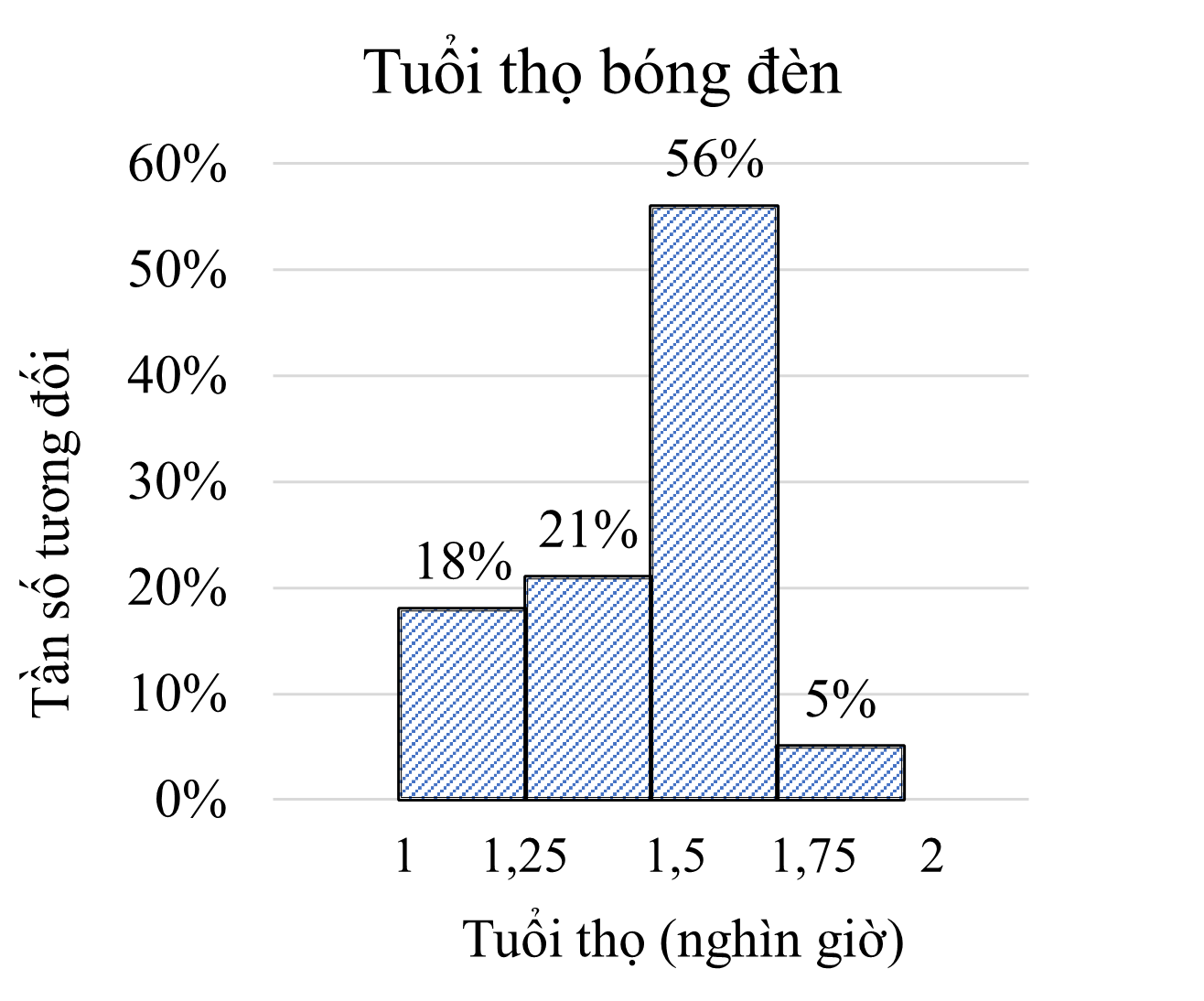
Tần số \[5\% \] là tần số tương đối của nhóm \[\left[ {1\,,75;2} \right)\].

Không gian mẫu của phép thử là: 

              = {(1, 2); (1, 3); (1, 4); (2, 1); (2, 3); (2, 4); (3, 1); (3, 2); (3, 4); (4, 1); (4, 2); (4, 3)}.

Số các kết quả có thể xảy ra (số phần tử của không gian mẫu) là  .

Gọi \(A\) là biến cố “Lấy được 2 viên bi mà tổng hai số trên hai viên bi đó là số lẻ”.

Số kết quả thuận lợi của biến cố \(A\) là  \(n(A) = 8\)

Xác suất của biến cố\(A\)  là \(p(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{8}{{12}} = \frac{2}{3}\).

1)   Thay \[x = 25\] (tmđk) vào \(B\)

  \[B = \frac{{5 - 2}}{{5 + 1}} = \frac{3}{6} = \frac{1}{2}\].

Vậy khi \(x = 25\)thì \[B = \frac{1}{2}\]

 2) A = \[\frac{{3\sqrt x  - 6 + \sqrt x  + (\sqrt x  - 3)(\sqrt x  - 2)}}{{\sqrt x (\sqrt x  - 2)}}\]

    \[ = \frac{{3\sqrt x  - 6 + \sqrt x  + x - 5\sqrt x  + 6}}{{\sqrt x (\sqrt x  - 2)}}\]\[ = \frac{{x - \sqrt x }}{{\sqrt x (\sqrt x  - 2)}}\]

    \[ = \frac{{\sqrt x (\sqrt x  - 1)}}{{\sqrt x (\sqrt x  - 2)}}\]\[ = \frac{{\sqrt x  - 1}}{{\sqrt x  - 2}}\]

3)  \[Q = A.B = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\]. ĐK để \[\sqrt Q \] xác định là \(Q \ge 0\)suy ra \(x \ge 1\)

\[\sqrt Q  < \frac{2}{3}\]

\[Q < \frac{4}{9}\]

\[\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} < \frac{4}{9}\]

\[\sqrt x  < \frac{{13}}{5}\]suy ra \[0 < x < \frac{{169}}{{25}}\]

Kết hợp điều kiện  x nguyên tìm được \[x \in \left\{ {1;\,2;3;4;5;6} \right\}\]

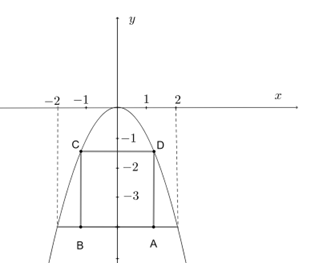
Đặt hệ trục tọa độ Oxy như hình vẽ. Parabol có dạng \(y = a{x^2}\left( {a < 0} \right)\)

Khoảng cách từ điểm cao nhất của cửa đến mặt đất là 4 mét, khoảng cách giữa hai chân cửa là 4 mét nên parabol đi qua điểm \[\left( {2; - 4} \right)\]

Suy ra:

 \[ - 4 = a{.2^2}\]

\[\,\,\,\,a =  - 1\]

Parabol có dạng \(y =  - {x^2}\)

Giả sử\[ABCD\]là hình chữ nhật có độ dài \[AB = CD = 2k\]

Khi đó 4 đỉnh của khung thép hình chữ nhật có tọa độ là:

\[A\left( {k;\, - 4} \right);\,\,B\left( { - k; - 4} \right);C\left( { - k;\,\,{k^2}} \right);D\left( {k;\,\,{k^2}} \right)\left( {k > 0} \right)\]

Suy ra \[AB = 2k;\,\,BC = 4 - {k^2}\]

Khi đó diện tích hình chữ nhật ABCD bằng \[2k\left( {4 - {k^2}} \right)\]

Ta có:

\[2k\left( {4 - {k^2}} \right) - \frac{{32}}{{3\sqrt 3 }}\]\( =  - 2\left( {{k^3} - 4k + \frac{{16}}{{3\sqrt 3 }}} \right)\)

\( =  - 2\left( {{k^2} - 2k.\frac{2}{{\sqrt 3 }} + \frac{4}{3}} \right).\left( {k + \frac{4}{{\sqrt 3 }}} \right)\)

\( =  - 2{\left( {k - \frac{2}{{\sqrt 3 }}} \right)^2}\left( {k + \frac{4}{{\sqrt 3 }}} \right) \le 0\) với \(k > 0\)

Suy ra

\[2k\left( {4 - {k^2}} \right) \le \frac{{32}}{{3\sqrt 3 }}\]

Dấu “=” có khi \(k = \frac{2}{{\sqrt 3 }}\)

Gọi số bảng đấu dự kiến ban đầu là x (bảng) \(\left( {x \in N*;\,x > 3} \right)\).

Số đội mỗi bảng ban đầu là \(\frac{{56}}{x}\)(đội)

Số đội tham dự thực tế là \(56 - 1 = 55\)(đội)

Tổng số bảng đấu giảm đi 3 bảng nên số bảng lúc sau là \(x - 3\)(bảng)

Số đội mỗi bảng lúc sau là \(\frac{{55}}{{x - 3}}\)(đội)

Vì tăng thêm mỗi bảng 1 đội nên ta có phương trình:\(\frac{{55}}{{x - 3}} - \frac{{56}}{x} = 1\)

\( \Rightarrow \frac{{ - x + 168}}{{x\left( {x - 3} \right)}} = 1 \Rightarrow {x^2} - 2x - 168 = 0\)

Giải phương trình tim được 2 nghiệm x1 = 14 (tm) hoặc x2 = -12 ( loại)

Vậy số bảng dự kiến ban đầu là 14 bảng đấu.

Gọi số tiền điện nhà bạn \(A\) phải trả trong tháng \(4\) là \[x{\rm{ }}\left( {x > 0} \right)\] (đồng)

Số tiền điện nhà bạn B phải trà trong tháng 4 là \(y \left( {y > 0} \right)\)  (đồng)

Theo bài ta có tổng số tiền điện trong tháng \(4\) nhà bạn \(A\) và nhà bạn \(B\) phải trả là \(560\,000\) nên ta có phương trình \(x + y = 560\,000\) \(\left( 1 \right)\)

Số tiền điện trong tháng \(5\) nhà bạn \(A\) phải trả là \(x + 30\% \,x = 1,3\,x\) (đồng)

Số tiền điện trong tháng \(5\) nhà bạn \(B\) phải trả là: \(y + 20\% \,y = 1,2\,y\) (đồng)

Theo bài ta có tổng số tiền điện trong tháng \(5\) nhà bạn \(A\) và nhà bạn \(B\) phải trả là \(701\,000\)nên ta có phương trình: \(1,3\,x + 1,2\,y = 701\,000\)\(\left( 2 \right)\)

Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y = 560\,000}\\{1,3x + 1,2y = 701\,000}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 290\,000}\\{y = 270\,000}\end{array}} \right.\)

Vậy số tiền điện nhà bạn \(A\) phải trả trong tháng \(4\) là \(290\,000\) đồng.

Nhận thấy: \(290\,000 = 100\,.\,1500 + 50\,.\,2000 + 10\,.\,4000\)

                           Vậy số điện nhà bạn \(A\) dùng trong tháng \(4\) là \(100 + 50 + 10 = 160\left( {kWh} \right)\).