(1,5 điểm) Cho các biểu thức
\[A = \frac{{3\sqrt x - 6}}{{x - 2\sqrt x }} - \frac{1}{{2 - \sqrt x }} + \frac{{\sqrt x - 3}}{{\sqrt x }}\] và \[B = \frac{{\sqrt x - 2}}{{\sqrt x + 1}}\] với \(x > 0;\,\,x \ne 4\)
1) Tính giá trị của \(B\) khi \(x = 25\)
2) Chứng minh \(Q = A.B\)=\[\frac{{\sqrt x - 1}}{{\sqrt x + 1}}\]
3) Tìm các số nguyên \(x\) để \[\sqrt Q < \frac{{\sqrt 4 }}{3}\]
(1,5 điểm) Cho các biểu thức
\[A = \frac{{3\sqrt x - 6}}{{x - 2\sqrt x }} - \frac{1}{{2 - \sqrt x }} + \frac{{\sqrt x - 3}}{{\sqrt x }}\] và \[B = \frac{{\sqrt x - 2}}{{\sqrt x + 1}}\] với \(x > 0;\,\,x \ne 4\)
1) Tính giá trị của \(B\) khi \(x = 25\)
2) Chứng minh \(Q = A.B\)=\[\frac{{\sqrt x - 1}}{{\sqrt x + 1}}\]
3) Tìm các số nguyên \(x\) để \[\sqrt Q < \frac{{\sqrt 4 }}{3}\]
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 26 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Thay \[x = 25\] (tmđk) vào \(B\)
\[B = \frac{{5 - 2}}{{5 + 1}} = \frac{3}{6} = \frac{1}{2}\].
Vậy khi \(x = 25\)thì \[B = \frac{1}{2}\]
2) A = \[\frac{{3\sqrt x - 6 + \sqrt x + (\sqrt x - 3)(\sqrt x - 2)}}{{\sqrt x (\sqrt x - 2)}}\]
\[ = \frac{{3\sqrt x - 6 + \sqrt x + x - 5\sqrt x + 6}}{{\sqrt x (\sqrt x - 2)}}\]\[ = \frac{{x - \sqrt x }}{{\sqrt x (\sqrt x - 2)}}\]
\[ = \frac{{\sqrt x (\sqrt x - 1)}}{{\sqrt x (\sqrt x - 2)}}\]\[ = \frac{{\sqrt x - 1}}{{\sqrt x - 2}}\]
3) \[Q = A.B = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}\]. ĐK để \[\sqrt Q \] xác định là \(Q \ge 0\)suy ra \(x \ge 1\)
\[\sqrt Q < \frac{2}{3}\]
\[Q < \frac{4}{9}\]
\[\frac{{\sqrt x - 1}}{{\sqrt x + 1}} < \frac{4}{9}\]
\[\sqrt x < \frac{{13}}{5}\]suy ra \[0 < x < \frac{{169}}{{25}}\]
Kết hợp điều kiện x nguyên tìm được \[x \in \left\{ {1;\,2;3;4;5;6} \right\}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
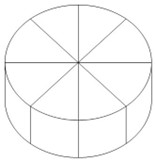
Hộp phô mai hình trụ có đường kính đáy \({\rm{10}}{\rm{,6}}\,{\rm{cm}}\) và chiều cao \({\rm{1}}{\rm{,5}}\,{\rm{cm}}\).
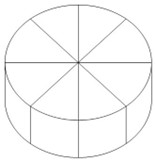
a) Biết rằng 8 miếng phô mai được xếp nằm sát bên trong hộp. Hỏi thể tích của một miếng phô mai là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất, lấy\(\pi \approx 3,14\))
Thể tích hộp phô mai là:\[V = h.\frac{1}{4}.\pi .{d^2} \approx 1,5.\frac{1}{4}{.3,14.10,6^2} = 132,3039\,(c{m^3})\].
Thể tích một miếng phô mai là: \[V' = \frac{{132,3039}}{8} \approx 16,5\,(c{m^3})\].
b) Diện tích xung quanh của một miếng phô mai là:
\[S = 2 \cdot \frac{d}{2} \cdot h + \frac{{d \cdot \pi \cdot h}}{8} + 2 \cdot \frac{{\frac{1}{4} \cdot \pi \cdot {d^2}}}{8}\]
\( \approx 10,6 \cdot 1,5 + \frac{{10,6 \cdot 3,14 \cdot 1,5}}{8} + \frac{{3,14 \cdot {{10,6}^2}}}{{16}} = 44,70815\,(c{m^2})\)
Diện tích giấy gói được sử dụng cho một miếng phô mai là:
\(\;\;\;\;\;\;\;\;\;\;\;\;\;S' = 44,70815:90\% \approx 49,7\,(c{m^2})\).
Lời giải
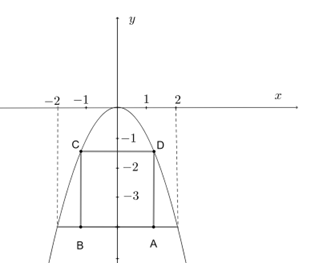
Đặt hệ trục tọa độ Oxy như hình vẽ. Parabol có dạng \(y = a{x^2}\left( {a < 0} \right)\)
Khoảng cách từ điểm cao nhất của cửa đến mặt đất là 4 mét, khoảng cách giữa hai chân cửa là 4 mét nên parabol đi qua điểm \[\left( {2; - 4} \right)\]
Suy ra:
\[ - 4 = a{.2^2}\]
\[\,\,\,\,a = - 1\]
Parabol có dạng \(y = - {x^2}\)
Giả sử\[ABCD\]là hình chữ nhật có độ dài \[AB = CD = 2k\]
Khi đó 4 đỉnh của khung thép hình chữ nhật có tọa độ là:
\[A\left( {k;\, - 4} \right);\,\,B\left( { - k; - 4} \right);C\left( { - k;\,\,{k^2}} \right);D\left( {k;\,\,{k^2}} \right)\left( {k > 0} \right)\]
Suy ra \[AB = 2k;\,\,BC = 4 - {k^2}\]
Khi đó diện tích hình chữ nhật ABCD bằng \[2k\left( {4 - {k^2}} \right)\]
Ta có:
\[2k\left( {4 - {k^2}} \right) - \frac{{32}}{{3\sqrt 3 }}\]\( = - 2\left( {{k^3} - 4k + \frac{{16}}{{3\sqrt 3 }}} \right)\)
\( = - 2\left( {{k^2} - 2k.\frac{2}{{\sqrt 3 }} + \frac{4}{3}} \right).\left( {k + \frac{4}{{\sqrt 3 }}} \right)\)
\( = - 2{\left( {k - \frac{2}{{\sqrt 3 }}} \right)^2}\left( {k + \frac{4}{{\sqrt 3 }}} \right) \le 0\) với \(k > 0\)
Suy ra
\[2k\left( {4 - {k^2}} \right) \le \frac{{32}}{{3\sqrt 3 }}\]
Dấu “=” có khi \(k = \frac{2}{{\sqrt 3 }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập