Đề thi tuyển sinh vào lớp 10 Toán năm học 2022 - 2023 Sở GD&ĐT TP.HCM có đáp án
46 người thi tuần này 4.6 161 lượt thi 8 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a)
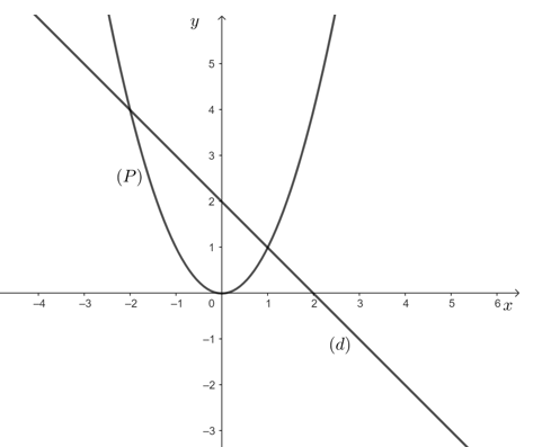
b) Ta có phương trình hoành độ giao điểm \(\left( P \right),\left( d \right)\) là
\({x^2} = - x + 2 \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = 1\\{x_2} = - 2\end{array} \right.\)
Với \({x_1} = 1 \Rightarrow {y_1} = 1 \Rightarrow A\left( {1;1} \right)\);
Với \[{x_2} = - 2 \Rightarrow {y_2} = 4 \Rightarrow B\left( { - 2;4} \right)\]
Vậy tọa độ giao điểm \(\left( P \right),\left( d \right)\)là \(A\left( {1;1} \right),B\left( { - 2;4} \right)\).
Lời giải
Ta có \(ac = 2.\left( { - 3} \right) = - 6 < 0\) nên phương trình luôn có hai nghiệm phân biệt.
Áp dụng hệ thức Vi-et ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - \frac{3}{2}\end{array} \right.\). Khi đó ta có:
\(A = {\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = {2^2} - 4.\frac{{ - 3}}{2} = 10\).
Lời giải
a) Chỉ số BMI của Hạnh là \(\frac{{50}}{{{{1,63}^2}}} \approx 18,8\) (kg/m2).
Vậy theo bảng phân loại chỉ số BMI, ta thấy Hạnh thuộc nhóm bình thường.
b) Do chỉ số BMI ở mức bình thường là từ 18,5 đến 24,9 nên:
+ Cân nặng tối thiểu của Phúc là \({18,5.1,73^2} \approx 55,4\,\,{\rm{(kg)}}\)
+ Cân nặng tối đa của Phúc là \({24,9.1,73^2} \approx 74,5\,\,{\rm{(kg)}}\)
Vậy cân nặng của Phúc trong khoảng 55,4 kg đến 74,5 kg thỉ chỉ số BMI của Phúc bình thường.
Lời giải
+ Nếu Hằng mua ở cửa hàng A thì Hằng phải mua 3 cái bánh với giá 15 000 đồng/cái và 10 cái bánh với giá \(75\% .15000\) đồng/cái nên Hằng cần trả số tiền là
\(3.15\,000 + 10.15\,000.75\% = 157\,500\) (đồng).
+ Nếu Hằng mua ở cửa hàng B cứ mua 3 bánh Hằng được tặng 1 cái bánh cùng loại nên nếu Hằng mua 9 bánh thì Hằng được tặng 3 chiếc và thiếu 1 chiếc cần mua với giá 15 000 đồng. Như thế, Hằng sẽ cần phải mua 10 cái bánh và số tiền Hằng cần trả là
\(9.\,15\,000 + 15\,000 = 150\,000\) (đồng).
Vậy bạn Hằng mua bánh ở cửa hàng B thì tiết kiệm hơn và tiết kiệm được \(157\,500 - 150\,000 = 7\,500\) đồng so với cửa hàng A.
Lời giải
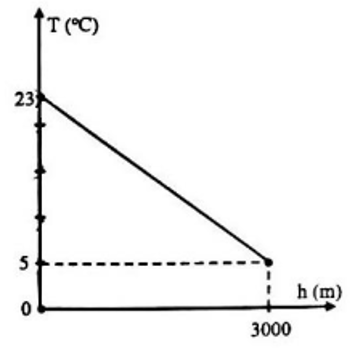
a) Ta có : \(T = ah + b\)
Quan sát đồ thị hàm số, đường thẳng \(T = ah + b\) đi qua điểm \(\left( {3000;5} \right)\)nên ta có phương trình \(3000a + b = 5\)
Vì ở chân núi , nhiệt độ không khí là \(23^\circ C\) nên ta có:
\(23 = 0.a + b \Leftrightarrow b = 23\)
Thay \(b = 23 \Rightarrow 3000a = 5 - 23 = - 18 \Leftrightarrow a = - 0,006\)
Vậy \(a = - 0,006;\,\,\,b = 23\).
b) Theo ý a ta có : \(T = - 0,006h + 23\)
Bạn Minh đang ở nhiệt độ \(15,8^\circ C\) so với chân núi nên thay \(T = 15,8\) vào ta có:
\(15,8 = - 0,006h + 23 \Leftrightarrow h = 1200\).
Vậy Minh đang ở độ cao 1200 m so với chân núi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.