Một đống cát có dạng hình nón có chu vi đáy là 25,12 m và độ cao là 1,5 m.
b) Người ta dùng xe cải tiến để vận chuyển đống cát đó đên khu xây dựng. Biết thùng chứa của xe cải tiến có dạng hình hộp chữ nhật có kích thước dài 1 m, rộng 6 dm và cao 3 dm. Trong mỗi chuyến xe, thùng xe có thể chứa nhiều hơn thể tích thực của nó là 10% để vận chuyển được nhiểu cát hơn. Hỏi cần ít nhất bao nhiêu chuyến xe cải tiến để chuyển hết đống cát trên?
Quảng cáo
Trả lời:
a) Hình nón có chu vi đáy là 25,12 m nên ta có:
\(C = 2\pi R = 25,12 \Leftrightarrow R = \frac{{25,12}}{{2.3,14}} = 4\,\,\left( {\rm{m}} \right)\).
Thể tích của đống cát trên: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}{.3,14.4^2}.1,5 = 25,12\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\).
Vậy thể tích của đống cát là \(25,12\,\,{{\rm{m}}^{\rm{3}}}\).
b) \({\rm{6}}\,{\rm{dm}}\,{\rm{ = }}\,{\rm{0}}{\rm{,6}}\,{\rm{m}}\,{\rm{;}}\,\,{\rm{3}}\,\,{\rm{dm}}\,{\rm{ = }}\,{\rm{0}}{\rm{,3}}\,{\rm{m}}\)
Thể tích của thùng chứa là: \(1.0,6.0,3 = 0,18\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\).
Trong mỗi chuyến xe, thùng xe có thể chứa: \(0,18 + 0,18.10\% = 0,198\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\).
Ta có: \(\frac{{25,12}}{{0,198}} \approx 126,9\), do đó để vận chuyển hết đống cát đã cho, cần 126 + 1 = 127 chuyến xe.
Vậy cần ít nhất 127 chuyến xe để chuyển hết đống cát.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì có năm đội bóng thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại) nên có tất cả \(\frac{{5.4}}{2} = 10\) trận đấy đã diễn ra ở bảng đấu trên.
b) Từ câu a, ta có tất cả 10 trận, gồm thắng - thua và hòa.
Gọi số trận thắng - thua là \(x\) trận, hòa là \(y\) trận \(\left( {x,y \in \mathbb{N}} \right)\).
Khi đó ta có \(x + y = 10\).
Mỗi trận thắng - thua có tổng số điểm là 3 nên tổng điểm các trận thắng - thua là \(3x\).
Mỗi trận hòa có tổng số điểm là 2 (mỗi đội được 1 điểm) nên tổng điểm là \(2y\).
Tổng số điểm của 10 trận đấu trên là \(3x + 2y = 10 + 9 + 6 + 4 + 0 = 29\).
Nên ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 10\\3x + 2y = 29\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 9\\y = 1\end{array} \right.(tm)\).
Như vậy có 1 trận hòa.
Giả sử đội nào đó có \(a\) trận thắng, 1 trận hòa và \(c\) trận thua.
Nên số điểm đội đó là \(3a + 1\) điểm nên số điểm của đội có 1 trận hòa phải chia 3 dư 1.
Ta thấy A và D thỏa mãn.
Vậy trận đấu hòa là trận đấu giữa đội A và đội D.
Lời giải
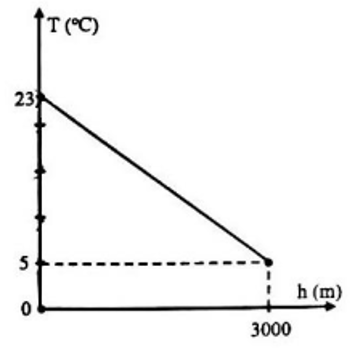
a) Ta có : \(T = ah + b\)
Quan sát đồ thị hàm số, đường thẳng \(T = ah + b\) đi qua điểm \(\left( {3000;5} \right)\)nên ta có phương trình \(3000a + b = 5\)
Vì ở chân núi , nhiệt độ không khí là \(23^\circ C\) nên ta có:
\(23 = 0.a + b \Leftrightarrow b = 23\)
Thay \(b = 23 \Rightarrow 3000a = 5 - 23 = - 18 \Leftrightarrow a = - 0,006\)
Vậy \(a = - 0,006;\,\,\,b = 23\).
b) Theo ý a ta có : \(T = - 0,006h + 23\)
Bạn Minh đang ở nhiệt độ \(15,8^\circ C\) so với chân núi nên thay \(T = 15,8\) vào ta có:
\(15,8 = - 0,006h + 23 \Leftrightarrow h = 1200\).
Vậy Minh đang ở độ cao 1200 m so với chân núi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.