Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\left( {AB < AC} \right)\). Gọi \(D\) là điểm trên cung nhỏ \(BC\) sao cho \(DB < DC.\) Từ \(D\) kẻ \(DE\) vuông góc với \(BC\) (\(E\) thuộc \(BC),\) kẻ \(DF\) vuông góc với \(AC\,\,\left( {F \in AC} \right)\). Đường thẳng \(EF\)cắt tia \(AB\) tại \(K\).
a) Chứng minh tứ giác \(CDEF\) nội tiếp và \(\widehat {DFE} = \widehat {DAB}\).
b) Chứng minh tứ giác \(DKBE\) nội tiếp và \(DB.DF = DA.DE\).
c) Gọi \(I,J\) lần lượt là trung điểm của \(AB,EF.\) Chứng minh \[IJ\] vuông góc với \(DJ\).
Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\left( {AB < AC} \right)\). Gọi \(D\) là điểm trên cung nhỏ \(BC\) sao cho \(DB < DC.\) Từ \(D\) kẻ \(DE\) vuông góc với \(BC\) (\(E\) thuộc \(BC),\) kẻ \(DF\) vuông góc với \(AC\,\,\left( {F \in AC} \right)\). Đường thẳng \(EF\)cắt tia \(AB\) tại \(K\).
a) Chứng minh tứ giác \(CDEF\) nội tiếp và \(\widehat {DFE} = \widehat {DAB}\).
b) Chứng minh tứ giác \(DKBE\) nội tiếp và \(DB.DF = DA.DE\).
c) Gọi \(I,J\) lần lượt là trung điểm của \(AB,EF.\) Chứng minh \[IJ\] vuông góc với \(DJ\).
Quảng cáo
Trả lời:

a)
Ta có: \(DE \bot BC \Rightarrow \widehat {DEC} = 90^\circ ,DF \bot AC \Rightarrow \widehat {DFC} = 90^\circ \).
Tứ giác \(CDEF\)có \(\widehat {DEC} = \widehat {DFC} = 90^\circ \) mà hai góc này có hai đỉnh kề nhau cùng nhìn \(CD\) dưới một góc không đổi nên tứ giác \(CDEF\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {DFE} = \widehat {DCE}\) (2 góc nội tiếp cùng chắn cung \(DE)\).
\( \Rightarrow \widehat {DFE} = \widehat {DCB}\).
Xét đường tròn \(\left( O \right)\) có \(\widehat {DAB} = \widehat {DCB}\) (2 góc nội tiếp cùng chắn cung \(BD\))
Suy ra \(\widehat {DFE} = \widehat {DAB}\) (đpcm).
b)
+ Ta có \(\widehat {DFE} = \widehat {DAB}(cmt) \Rightarrow \widehat {DFK} = \widehat {DAK}\).
Tứ giác \(AKDF\) có \(\widehat {DFK} = \widehat {DAK}(cmt)\) mà hai góc này có 2 đỉnh kề nhau cùng nhìn \(DK\) dưới một góc không đổi nên \(AKDF\) là tứ giác không đổi.
\( \Rightarrow \widehat {AFD} + \widehat {AKD} = 180^\circ \) (tổng hai góc đối nhau).
Mà \(\widehat {AFD} = 90^\circ \) (do \(DF \bot AC\)) \( \Rightarrow 90^\circ + \angle AKD = 180^\circ \Rightarrow \widehat {AKD} = 90^\circ \Rightarrow \widehat {BKD} = 90^\circ \).
Ta có \(DE \bot BC\) tại \(E\) \( \Rightarrow \widehat {DEB} = 90^\circ \).
Xét tứ giác \(DKBE\) có \(\widehat {BKD} + \widehat {BED} = 90^\circ + 90^\circ = 180^\circ \) mà hai góc này đối nhau
Nên \(DKBE\) là tứ giác nội tiếp.
+ Xét đường tròn \(\left( O \right)\) có \(\widehat {ADB} = \widehat {ACB}\) (cùng chắn cung \(AB\)) \( \Rightarrow \widehat {ADB} = \widehat {ECF}\)
Tứ giác \(CDEF\) nội tiếp (cmt) \( \Rightarrow \widehat {ECF} = \widehat {EDF}\) (cùng chắn cung \(EF\))
\( \Rightarrow \widehat {ADB} = \widehat {EDF}\).
Xét \(\Delta ABD\) và \(\Delta FED\) có:
\( \Rightarrow \frac{{DA}}{{DF}} = \frac{{DB}}{{DE}} \Rightarrow DB.DF = DA.DE\,\,(dpcm)\).
c) Ta có
Ta có: \(I\) là trung điểm \(AB\) (gt) \( \Rightarrow AB = 2BI\), \(J\) là trung điểm \(EF\)\( \Rightarrow EF = 2EJ\)
Lại có \(\Delta ABD \sim \Delta FED(cmt) \Rightarrow \frac{{AB}}{{EF}} = \frac{{BD}}{{DE}} \Rightarrow \frac{{2BI}}{{2EJ}} = \frac{{BD}}{{DE}}\) hay \(\frac{{BI}}{{EJ}} = \frac{{BD}}{{DE}}\).
Xét \(\Delta IBD\)và \(\Delta JED\)có:
\( \Rightarrow \widehat {BID} = \widehat {EJD} \Rightarrow \widehat {KID} = \widehat {KJD}\)
Tứ giác \(IKDJ\)có \(\widehat {KID} = \widehat {KJD}\,(cmt)\)mà hai góc này cùng nhìn \(DK\) dưới 1 góc không đổi nên \(IKDJ\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {IKD} + \widehat {IJD} = 180^\circ \) (tổng 2 góc đối của tứ giác nội tiếp)
Mà \(\widehat {IKD} = 90^\circ \,\,\,\left( {do\,\,\widehat {BKD} = 90^\circ \left( {cmt} \right)} \right)\)
\( \Rightarrow \widehat {IJD} = 180^\circ - 90^\circ = 90^\circ \).
Vậy \(IJ \bot DJ\,\,(dpcm)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì có năm đội bóng thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại) nên có tất cả \(\frac{{5.4}}{2} = 10\) trận đấy đã diễn ra ở bảng đấu trên.
b) Từ câu a, ta có tất cả 10 trận, gồm thắng - thua và hòa.
Gọi số trận thắng - thua là \(x\) trận, hòa là \(y\) trận \(\left( {x,y \in \mathbb{N}} \right)\).
Khi đó ta có \(x + y = 10\).
Mỗi trận thắng - thua có tổng số điểm là 3 nên tổng điểm các trận thắng - thua là \(3x\).
Mỗi trận hòa có tổng số điểm là 2 (mỗi đội được 1 điểm) nên tổng điểm là \(2y\).
Tổng số điểm của 10 trận đấu trên là \(3x + 2y = 10 + 9 + 6 + 4 + 0 = 29\).
Nên ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 10\\3x + 2y = 29\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 9\\y = 1\end{array} \right.(tm)\).
Như vậy có 1 trận hòa.
Giả sử đội nào đó có \(a\) trận thắng, 1 trận hòa và \(c\) trận thua.
Nên số điểm đội đó là \(3a + 1\) điểm nên số điểm của đội có 1 trận hòa phải chia 3 dư 1.
Ta thấy A và D thỏa mãn.
Vậy trận đấu hòa là trận đấu giữa đội A và đội D.
Lời giải
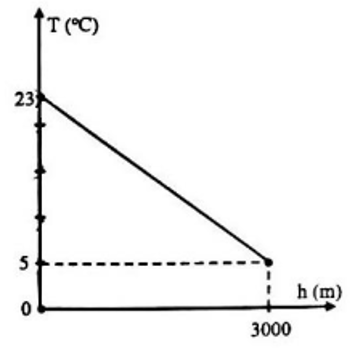
a) Ta có : \(T = ah + b\)
Quan sát đồ thị hàm số, đường thẳng \(T = ah + b\) đi qua điểm \(\left( {3000;5} \right)\)nên ta có phương trình \(3000a + b = 5\)
Vì ở chân núi , nhiệt độ không khí là \(23^\circ C\) nên ta có:
\(23 = 0.a + b \Leftrightarrow b = 23\)
Thay \(b = 23 \Rightarrow 3000a = 5 - 23 = - 18 \Leftrightarrow a = - 0,006\)
Vậy \(a = - 0,006;\,\,\,b = 23\).
b) Theo ý a ta có : \(T = - 0,006h + 23\)
Bạn Minh đang ở nhiệt độ \(15,8^\circ C\) so với chân núi nên thay \(T = 15,8\) vào ta có:
\(15,8 = - 0,006h + 23 \Leftrightarrow h = 1200\).
Vậy Minh đang ở độ cao 1200 m so với chân núi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.