Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 23

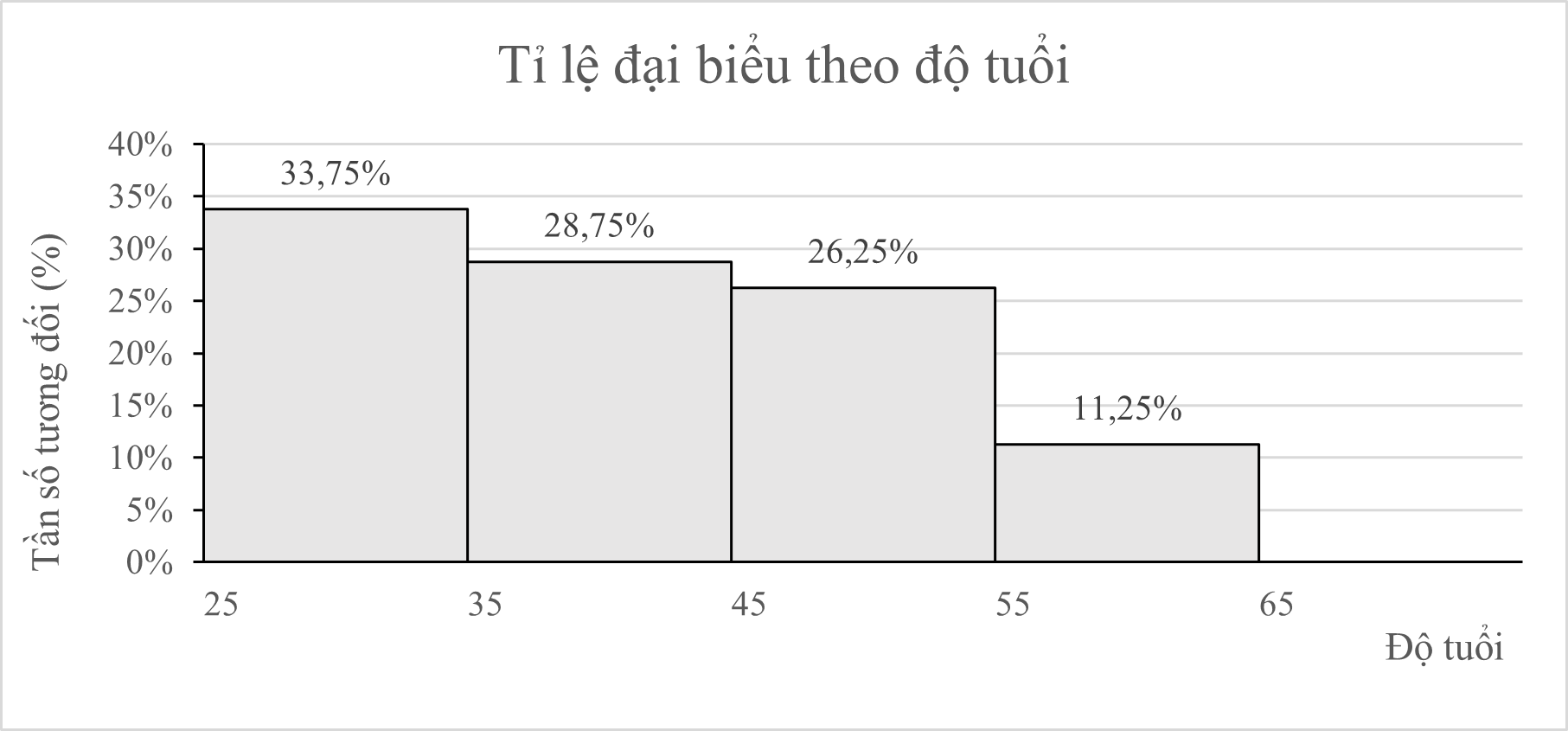
1a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.

Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)

Vậy tổng số đại biểu tham dự hội nghị là 160 người.

b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:

\[33,75\%  + 28,75\%  = 62,5\%  > 50\% .\]

Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.

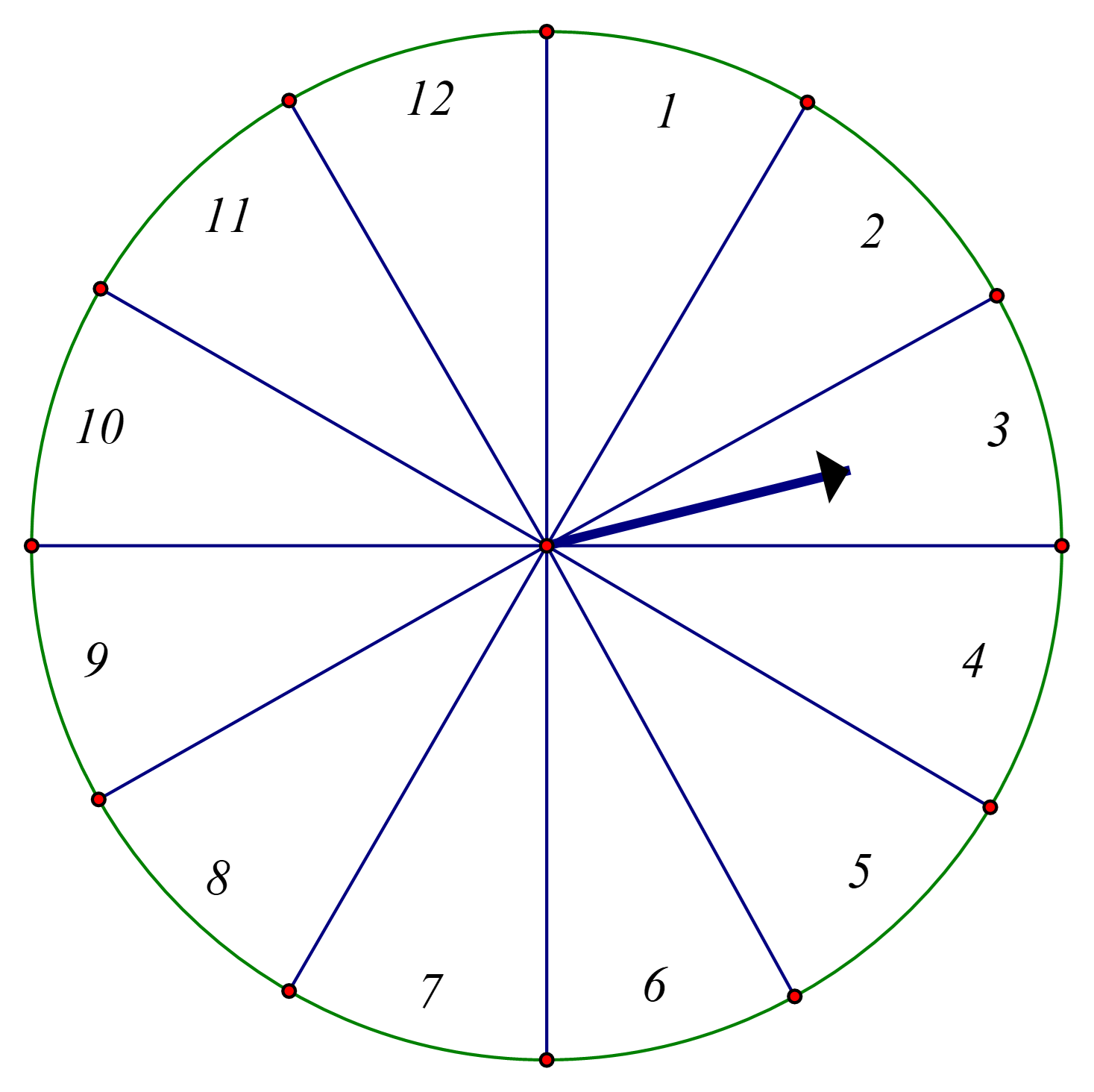
Có \[12\] kết quả có thể xảy ra khi quay ngẫu nhiên tấm bìa một lần.

\[A = \left\{ {1;\,\,2;\,\,3;\,\,...\,\,;\,\,12} \right\}\]

Có \[5\] kết quả thuận lợi cho biến cố B là: \[2;\,\,3;\,\,5;\,\,7;\,\,11 & \].

Vậy xác suất của biến \[P\] cố là: \[\frac{5}{{12}}\].

a) Khi \(x = 4\) (thỏa mãn điều kiện), ta thay vào biểu thức \(A\) ta có \(A = \frac{{4 + 2\sqrt 4 }}{4} = 2\).

Vậy \(A = 2\) khi \(x = 4\).

b) Ta có \[B = \frac{{\sqrt x  - 1}}{{\sqrt x }} + \frac{{2\sqrt x  + 1}}{{x + \sqrt x }} = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right) + 2\sqrt x  + 1}}{{\sqrt x \left( {\sqrt x  + 1} \right)}} = \frac{{x + 2\sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}} = \frac{{\sqrt x  + 2}}{{\sqrt x  + 1}}\]

Vậy với \(x > 0\) thì \[B = \frac{{\sqrt x  + 2}}{{\sqrt x  + 1}}\].

c) Với \(x > 0\), \(\frac{A}{B} = \frac{{x + 2\sqrt x }}{x}:\frac{{\sqrt x  + 2}}{{\sqrt x  + 1}} = \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{x}.\frac{{\sqrt x  + 1}}{{\sqrt x  + 2}} = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{x} = \frac{{x + \sqrt x }}{x}\)

Ta có: \(\frac{A}{B} < \frac{7}{4}\)

  \(\frac{{x + \sqrt x }}{x} < \frac{7}{4}\)

  \(1 + \frac{1}{{\sqrt x }} < \frac{7}{4}\)

       \(\frac{1}{{\sqrt x }} < \frac{3}{4}\)

        \(\sqrt x  > \frac{4}{3}\)

         \(x > \frac{{16}}{9}\)

Vậy số nguyên \(x\) nhỏ nhất thỏa điều kiện bài toán là \(x = 2\).

Trường hợp 1. Nếu thiết kế bao bì dạng hình trụ.

 Ta gọi, \(R\): bán kính hình trụ; \(l\): chiều cao hình trụ

Thể tích của hình trụ là: \(V\, = \,\pi {R^2}l\, = \,100\,\left( {{\rm{ml}}} \right)\)

Diện tích toàn phần của hình trụ là: \({S_{tp}}\, = \,2\pi Rl\, + \,2\pi {R^2}\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\)

Áp dụng bất đẳng thức Cauchy cho ba số không âm: \(\pi Rl\,;\,\,\pi Rl\,;\,\,2\pi {R^2}\) ta được

\({S_{tp}}\,\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\, \ge \,3\sqrt[3]{{\pi Rl\,.\,\pi Rl\,.2\pi {R^2}}}\,\, = \,3\sqrt[3]{{2\pi \,\,.{{\left( {\pi {R^2}l} \right)}^2}}}\,\)    

\({S_{tp}} \ge \,\,3\sqrt[3]{{2\pi \,.\,{{100}^2}}}\, \approx \,119,27\)        \(\left( 1 \right)\)

Dấu \('' = ''\) xảy ra khi \(\pi Rl\, = \,\pi Rl\, = \,2\pi {R^2}\,\, \Leftrightarrow \,\,l\, = \,2R\)

Trường hợp 2. Nếu thiết kế bao bì dạng hình hộp chữ nhật có đáy là hình vuông

Ta gọi, \(a\) là độ dài cạnh đáy của hình hộp chữ nhật; \(h\)là chiều cao của hình hộp chữ nhật.

Thể tích của hình hộp chữ nhật là: \(V\,\, = \,{a^2}.h\, = \,100\,\;{\rm{ml}}\)

Diện tích toàn phần của hình hộp chữ nhật là: \({S_{tp}}\, = \,2{a^2}\, + \,4ah\, = \,2{a^2}\, + \,2ah\, + \,2ah\)

Áp dụng b.đ.t Cô-Si cho ba số không âm :\(2{a^2}\,;\,2ah\,;\,2ah\)ta được:

\({S_{tp}}\, = \,2{a^2}\, + \,2ah\, + \,2ah\,\, \ge \,3\sqrt[2]{{2{a^2}.2ah\,.\,2ah}}\, = \,3\sqrt[3]{{8{a^2}h.{a^2}h}}\)

\({S_{tp}}\, \ge \,3.2.\,\sqrt[3]{{{{100}^2}}}\, \approx \,\,129,27\,\,\,\,\,\,\,\)\(\left( 2 \right)\)

Từ (1) và (2) suy ra, thiết kế hộp sữa dạng hình trụ có chiều cao gấp 2 lần bán kính đáy thì tốn ít nguyên vật liệu nhất.

Gọi x, y là số tiền phải trả cho mỗi loại hàng khi chưa tính thuế VAT (triệu đồng, x; y > 0)

* Khi tính thuế 10% và 8% lần lượt đối với mặt hàng thứ nhất và mặt hàng thứ hai thì số tiền phải trả cho loại hàng thứ nhất là \[x + 0,1x = 1,1x\] triệu đồng; số tiền phải trả cho loại hàng thứ hai là \[y + 0,08y = 1,08y\] triệu đồng

Tổng số tiền phải trả là \(2,17\)triệu đồng nên ta có phương trình \[1,1x + 1,08y = 2,17\]  (1)

* Khi tính thế \(9\% \) đối với cả hai loại hàng thì số tiền phải trả cho loại hàng thứ nhất là \[x + 0,09x = 1,09x\] triệu đồng và số tiền phải trả cho loại hàng thứ hai là \[y + 0,09y = 1,09y\] triệu đồng.

Tổng số tiền phải trả là \(2,18\) triệu đồng nên ta có phương trình \[1,09x + 1,09y = 2,18\]  (2)

Ta có hệ phương trình \(\left\{ \begin{array}{l}1,1x + 1,08y = 2,17\\1,09x + 1,09y = 2,18\end{array} \right.\)

Giải hệ ta được nghiệm duy nhất \(\left\{ \begin{array}{l}x = 0,5\\y = 1,5\end{array} \right.\) (thoả mãn)

Vậy khi chưa tính tiền thuế VAT thì giá của loại hàng thứ nhất là \[0,5\]triệu đồng và giá của loại hàng thứ hai là \[1,5\]triệu đồng

Gọi vận tốc đạp xe trung bình của Nam lúc đi từ nhà đến trường là x (km/h,\[x > 0\])

Thời gian đạp xe của Nam lúc đi từ nhà đến trường là \(\frac{4}{x}\)(h)

Vận tốc đạp xe trung bình của Nam lúc đi từ trường về nhà là \[x + 2\](km/h).

Thời gian đạp xe của Nam lúc đi từ trường về nhà là \(\frac{4}{{x + 2}}\)(h)

Lập luận để có phương trình: \(\frac{4}{x} + \frac{4}{{x + 2}} = \frac{{11}}{{15}}\)

Giải phương trình tìm được x = 10 (thoả mãn) hoặc \(x = \frac{{ - 12}}{{11}}\)(không thoả mãn)

Vậy vận tốc đạp xe trung bình của Nam lúc đi từ nhà đến trường là 10 km/h