(4,0 điểm)
Tính lượng vải cần mua để tạo ra nón của chú hề với các số liệu trong hình bên. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may nón là 15%. Cho biết \[\pi \approx 3,14\].
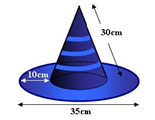
Tính lượng vải cần mua để tạo ra nón của chú hề với các số liệu trong hình bên. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may nón là 15%. Cho biết \[\pi \approx 3,14\].

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 23 !!
Quảng cáo
Trả lời:
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: \(r = \frac{{35 - 2.10}}{2} = 7,5\) (cm)
Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl = \pi .7,5.30 = 225\pi \)(cm2)
Diện tích vành nón (hình vành khăn): \(\pi .{\left( {\frac{{35}}{2}} \right)^2} - \pi .{\left( {7,5} \right)^2} = 250\pi \) (cm2)
Diện tích vải cần để may: \(225\pi + 250\pi = 475\pi \)(cm2).
Vì tỉ lệ vải khâu (may) hao (tốn) khi may nón là \[15\% \]nên diện tích vải thực tế cần dùng là:
\(475\pi + 15\% .475\pi = 546,25\pi \approx 546,25.3,14 = 1715,225\) (cm2).
Câu hỏi cùng đoạn
Câu 2:
Cho nửa \((O)\)đường kính \(AB = 2R\),\(C\) là điểm bất kì nằm trên nửa đường tròn sao cho\(C\) khác \(A\) và \(AC < CB\). Điểm \(D\) thuộc cung nhỏ \(BC\) sao cho: \(\widehat {COD} = {90^0}\). Gọi \(E\) là giao điểm của \(AD\) và \(BC\), \(F\) là giao điểm của \(AC\) và \(BD\), I là trung điểm của \[{\rm{EF}}\].
a) Chứng minh: \(CEDF\) là tứ giác nội tiếp.
b) Chứng minh: \(FC.FA = FD.FB\) .
c) Chứng minh \(IC\) là tiếp tuyến của \((O)\).
d) Hỏi khi \(C\) thay đổi thỏa mãn điều kiện bài toán, \(E\) thuộc đường tròn cố định nào?
Cho nửa \((O)\)đường kính \(AB = 2R\),\(C\) là điểm bất kì nằm trên nửa đường tròn sao cho\(C\) khác \(A\) và \(AC < CB\). Điểm \(D\) thuộc cung nhỏ \(BC\) sao cho: \(\widehat {COD} = {90^0}\). Gọi \(E\) là giao điểm của \(AD\) và \(BC\), \(F\) là giao điểm của \(AC\) và \(BD\), I là trung điểm của \[{\rm{EF}}\].
a) Chứng minh: \(CEDF\) là tứ giác nội tiếp.
b) Chứng minh: \(FC.FA = FD.FB\) .
c) Chứng minh \(IC\) là tiếp tuyến của \((O)\).
d) Hỏi khi \(C\) thay đổi thỏa mãn điều kiện bài toán, \(E\) thuộc đường tròn cố định nào?
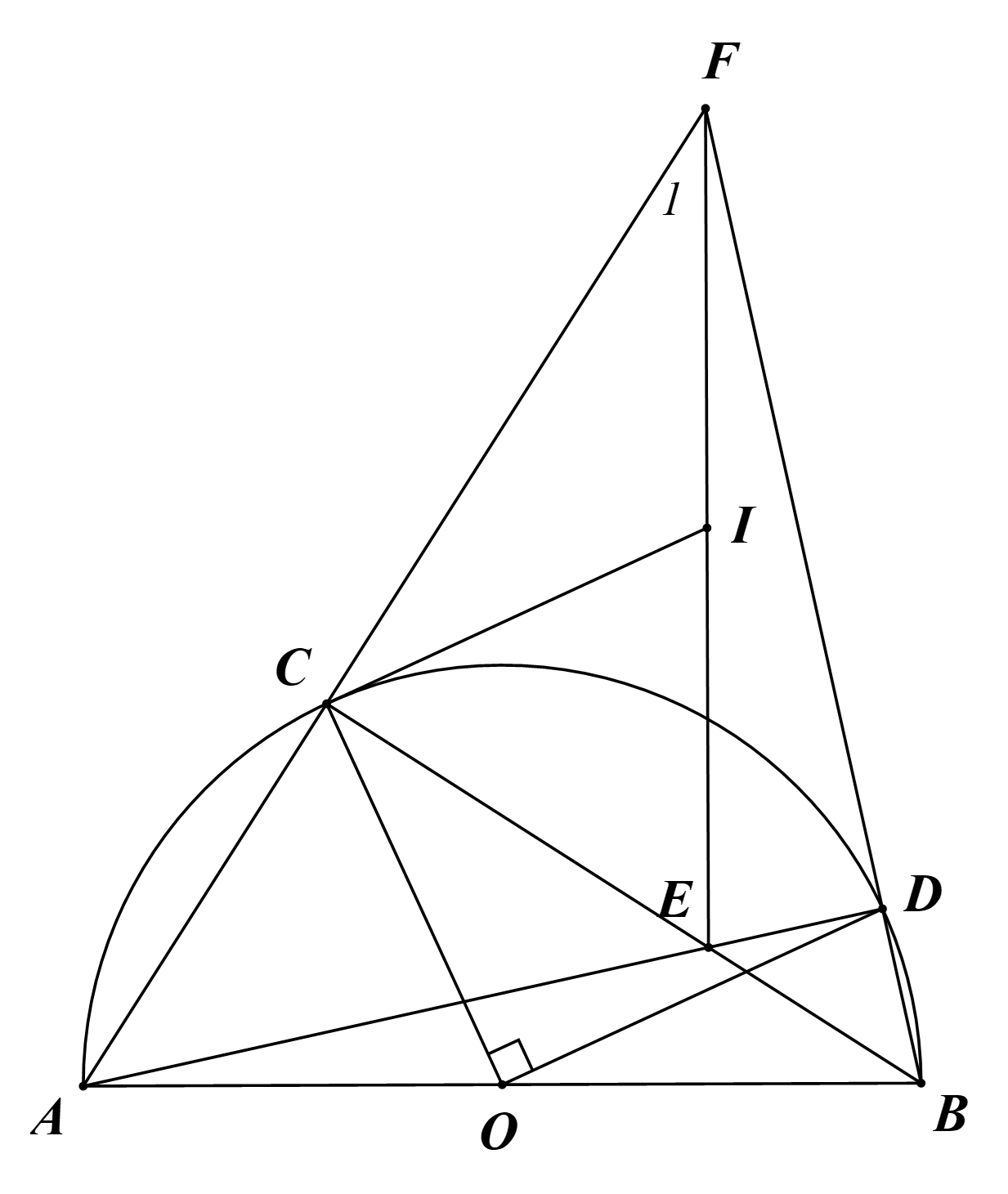
a) Giả sử \(I\) là trung điểm của \(EF\).
Xét \(\left( O \right)\) có:
\(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(BC \bot AF\)
Nên \(\Delta BCF\) hay \(\Delta ECF\)vuông tại \(C\), có \(CI\) là đường trung tuyến nên \(CI = IE = IF = \frac{{EF}}{2}\).
\(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \[AD \bot BF\].
Nên \(\Delta ADF\)hay \(\Delta EDF\)vuông tại C, có DI là đường trung tuyến nên \(DI = IE = IF = \frac{{EF}}{2}\).
Khi đó \(CI = DI = IE = IF\) suy ra tứ giác \(FCED\) nội tiếp đường tròn tâm \(I\) đường kính \(EF\).
b) Tam giác vuông \(FDA\) đồng dạng với tam giác vuông \(FCB\) (g.g).
Suy ra \(\frac{{FA}}{{FB}} = \frac{{FD}}{{FC}}\) (2 cặp cạnh tương ứng)
Nên \(FC.FA = FD.FB\) (đpcm)
c) Vì \(I\) là tâm đường tròn ngoại tiếp tứ giác \(FCED\) nên \[CI = IF\].
Khi đó \(\Delta ICF\)cân tại \(I\)\( \Rightarrow \widehat {{F_1}} = \widehat {FCI}\) (1)
Xét \(\Delta OAC\) cân tại \[O\] nên \(\widehat {CAO} = \widehat {OCA}\) (2)
Xét \(\Delta ABF\) có \[BC,AD\] là hai đường cao cắt nhau tại \[E\] nên \[E\] là trực tâm của \(\Delta ABF\).
Suy ra \[EF \bot AB\]\[ \Rightarrow \widehat {{F_1}} + \widehat {CAO} = {90^0}\] (3)
Từ (1); (2); (3) nên \(\widehat {ICF} + \widehat {OCA} = {90^0}\).
Do đó \(\widehat {OCI} = {90^o}\) hay \(OC \bot CI\).
Vậy \(CI\) là tiếp tuyến của đường tròn \(\left( O \right)\).
d) Ta có: \(\left. \begin{array}{l}\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \\\widehat {{O_2}} = 90^\circ \end{array} \right\}\) nên \(\widehat {\,{O_1}} + \widehat {{O_3}} = 90^\circ \).
Xét \(\left( O \right)\) ta có:
\[\left. \begin{array}{l}\widehat {DAB} = \frac{1}{2}\widehat {{O_1}}\\\widehat {ABC} = \frac{1}{2}\widehat {{O_3}}\end{array} \right\}\,\] nên \[\widehat {DAB} + \widehat {ABC} = \frac{1}{2} \cdot 90^\circ = 45^\circ \].
Xét \(\Delta AEB\) ta có \[\widehat {DAB} + \widehat {ABC} = 45^\circ \] nên \(\widehat {AEB} = 135^\circ \).
Qua A kẻ \(Ax \bot AE\) . Qua B kẻ \(By \bot BE\) ; Gọi By cắt Ax tại K.
Xét tứ giác \[EAKB\] ta có:
\(\left. \begin{array}{l}\widehat {KAE} = 90^\circ \left( {Ax \bot AE} \right)\\\widehat {KBE} = 90^\circ \left( {By \bot {\rm B}{\rm E}} \right)\end{array} \right\}\,\,n\^e n\,\,\widehat {KAE} + \widehat {KBE} = 180^\circ \).
Mà hai góc nằm tại hai đỉnh đối nhau nên tứ giác \[EAKB\] nội tiếp.
\(\widehat {AKB} + \widehat {AEB} = 180^\circ \) nên \(\,\widehat {AKB} = 45^\circ \).
Gọi H là trung điểm của EK nên \(H\) là tâm đường tròn ngoại tiếp tứ giác \[EAKB\].
Xét \(\left( H \right)\): \(\widehat {AKB} = \frac{1}{2}\widehat {AHB} \Rightarrow \widehat {AHB} = 90^\circ \).
Xét \(\Delta AHB\) vuông tại \(H\) có \(HA = HB\)(bán kính đường tròn tâm \(H\)) nên \[\Delta AHB\]vuông cân tại \(H\).
Mà \(AB\) không đổi nên \(H\) cố định.
Áp dụng định lí Pythagore vào \[\Delta AHB\] ta có: \(H{A^2} + H{B^2} = A{B^2}\)
\(\begin{array}{l}\,2H{A^2} = 4{R^2}\\\,\,\,H{A^2} = 2{R^2}\\\,\,\,\,\,HA = \sqrt 2 R\end{array}\)
Vậy khi \(C\) thay đổi thì \(E\) chạy trên đường tròn (H; \(\sqrt 2 R\)) cố định.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trường hợp 1. Nếu thiết kế bao bì dạng hình trụ.
Ta gọi, \(R\): bán kính hình trụ; \(l\): chiều cao hình trụ
Thể tích của hình trụ là: \(V\, = \,\pi {R^2}l\, = \,100\,\left( {{\rm{ml}}} \right)\)
Diện tích toàn phần của hình trụ là: \({S_{tp}}\, = \,2\pi Rl\, + \,2\pi {R^2}\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\)
Áp dụng bất đẳng thức Cauchy cho ba số không âm: \(\pi Rl\,;\,\,\pi Rl\,;\,\,2\pi {R^2}\) ta được
\({S_{tp}}\,\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\, \ge \,3\sqrt[3]{{\pi Rl\,.\,\pi Rl\,.2\pi {R^2}}}\,\, = \,3\sqrt[3]{{2\pi \,\,.{{\left( {\pi {R^2}l} \right)}^2}}}\,\)
\({S_{tp}} \ge \,\,3\sqrt[3]{{2\pi \,.\,{{100}^2}}}\, \approx \,119,27\) \(\left( 1 \right)\)
Dấu \('' = ''\) xảy ra khi \(\pi Rl\, = \,\pi Rl\, = \,2\pi {R^2}\,\, \Leftrightarrow \,\,l\, = \,2R\)
Trường hợp 2. Nếu thiết kế bao bì dạng hình hộp chữ nhật có đáy là hình vuông
Ta gọi, \(a\) là độ dài cạnh đáy của hình hộp chữ nhật; \(h\)là chiều cao của hình hộp chữ nhật.
Thể tích của hình hộp chữ nhật là: \(V\,\, = \,{a^2}.h\, = \,100\,\;{\rm{ml}}\)
Diện tích toàn phần của hình hộp chữ nhật là: \({S_{tp}}\, = \,2{a^2}\, + \,4ah\, = \,2{a^2}\, + \,2ah\, + \,2ah\)
Áp dụng b.đ.t Cô-Si cho ba số không âm :\(2{a^2}\,;\,2ah\,;\,2ah\)ta được:
\({S_{tp}}\, = \,2{a^2}\, + \,2ah\, + \,2ah\,\, \ge \,3\sqrt[2]{{2{a^2}.2ah\,.\,2ah}}\, = \,3\sqrt[3]{{8{a^2}h.{a^2}h}}\)
\({S_{tp}}\, \ge \,3.2.\,\sqrt[3]{{{{100}^2}}}\, \approx \,\,129,27\,\,\,\,\,\,\,\)\(\left( 2 \right)\)
Từ (1) và (2) suy ra, thiết kế hộp sữa dạng hình trụ có chiều cao gấp 2 lần bán kính đáy thì tốn ít nguyên vật liệu nhất.
Lời giải
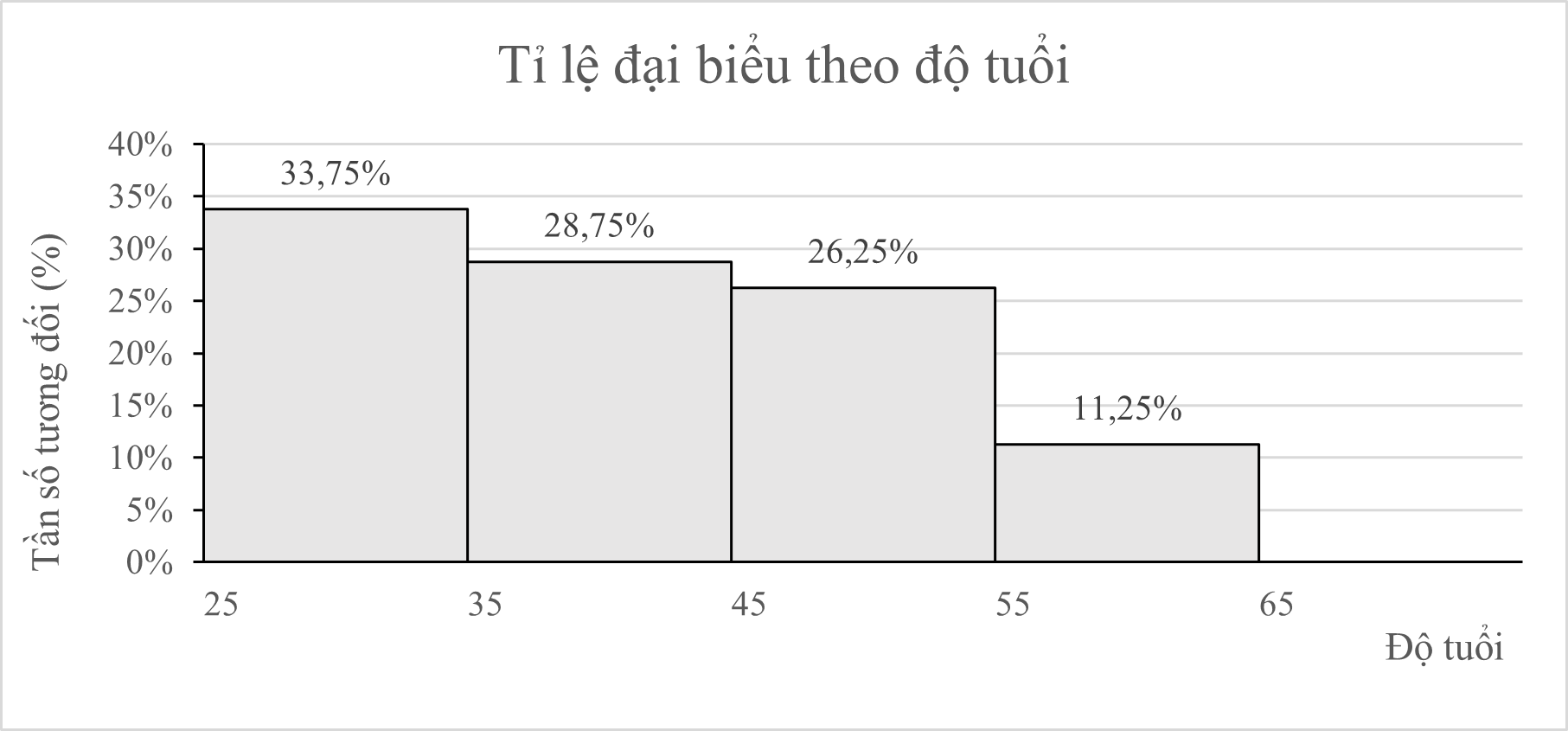
1a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.
Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)
Vậy tổng số đại biểu tham dự hội nghị là 160 người.
b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:
\[33,75\% + 28,75\% = 62,5\% > 50\% .\]
Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.