(1,5 điểm)
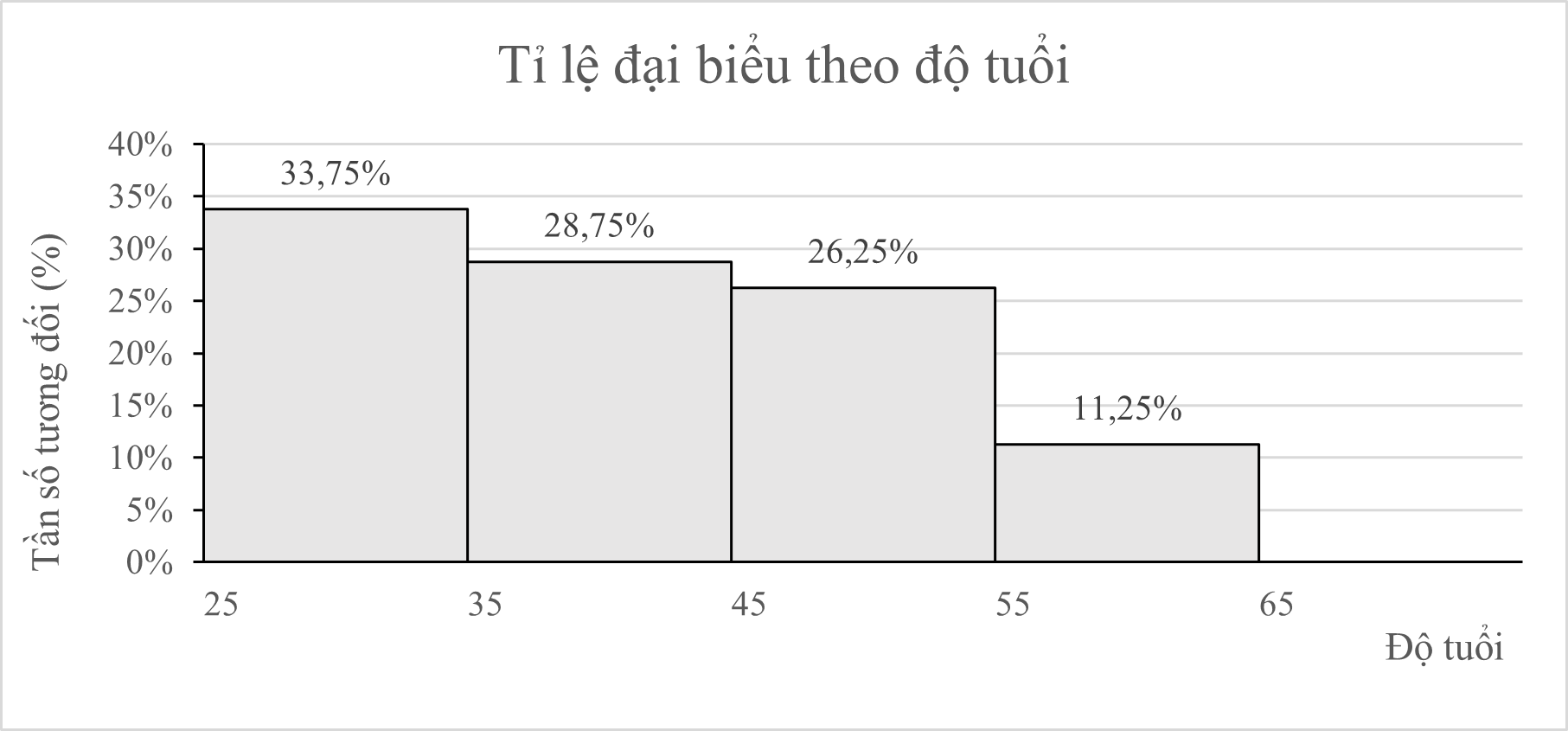
Để chuẩn bị cho tiết mục kỉ niệm 70 năm Chiến thắng Điện Biên Phủ, phường Mỹ Đình có cử một số lượng người tham gia, được biểu diễn dưới biểu đồ tỉ lệ sau:
( Biết rằng có 54 người từ 25 tuổi đến 35 tuổi)
a) Có bao nhiêu người tham gia biểu diễn?
b) Một người cho rằng có trên \[50\% \] số người biểu diễn dưới\[45\]tuổi. Nhận định đó đúng hay sai? Tại sao?
Để chuẩn bị cho tiết mục kỉ niệm 70 năm Chiến thắng Điện Biên Phủ, phường Mỹ Đình có cử một số lượng người tham gia, được biểu diễn dưới biểu đồ tỉ lệ sau:
( Biết rằng có 54 người từ 25 tuổi đến 35 tuổi)

a) Có bao nhiêu người tham gia biểu diễn?
b) Một người cho rằng có trên \[50\% \] số người biểu diễn dưới\[45\]tuổi. Nhận định đó đúng hay sai? Tại sao?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 23 !!
Quảng cáo
Trả lời:
1a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.
Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)
Vậy tổng số đại biểu tham dự hội nghị là 160 người.
b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:
\[33,75\% + 28,75\% = 62,5\% > 50\% .\]
Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.
Câu hỏi cùng đoạn
Câu 2:
Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia thành \(12\) phần bằng nhau và ghi các số \(1;2;3;...;12\). Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
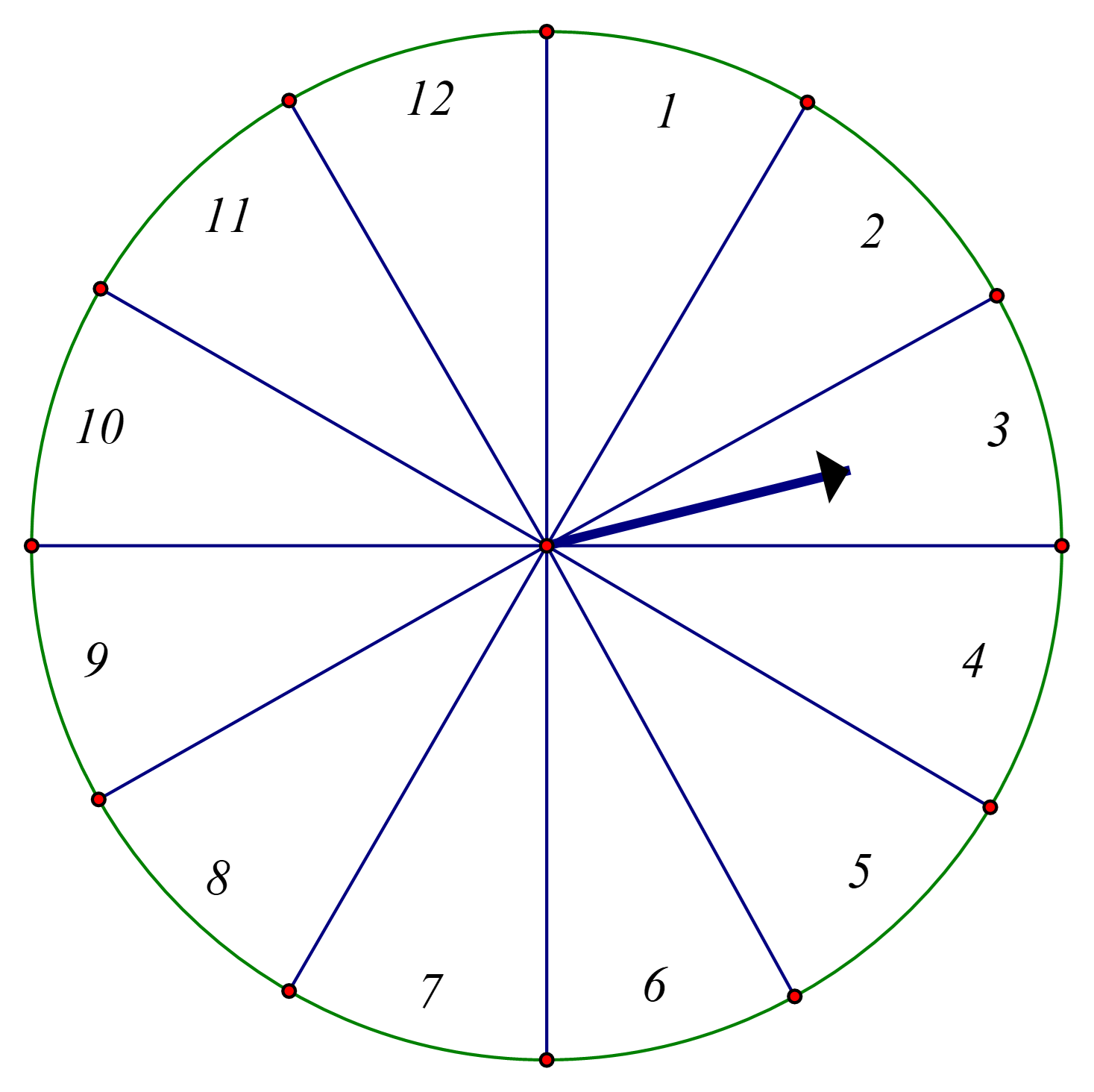
Xét phép thử: “Quay đĩa tròn một lần” và biến cố \(P:\) “Chiếc kim chỉ vào hình quạt ghi số là số nguyên tố”. Tính xác suất của biến cố \(P\).
Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia thành \(12\) phần bằng nhau và ghi các số \(1;2;3;...;12\). Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

Xét phép thử: “Quay đĩa tròn một lần” và biến cố \(P:\) “Chiếc kim chỉ vào hình quạt ghi số là số nguyên tố”. Tính xác suất của biến cố \(P\).
Có \[12\] kết quả có thể xảy ra khi quay ngẫu nhiên tấm bìa một lần.
\[A = \left\{ {1;\,\,2;\,\,3;\,\,...\,\,;\,\,12} \right\}\]
Có \[5\] kết quả thuận lợi cho biến cố B là: \[2;\,\,3;\,\,5;\,\,7;\,\,11 & \].
Vậy xác suất của biến \[P\] cố là: \[\frac{5}{{12}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
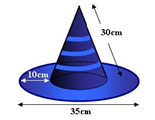
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: \(r = \frac{{35 - 2.10}}{2} = 7,5\) (cm)
Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl = \pi .7,5.30 = 225\pi \)(cm2)
Diện tích vành nón (hình vành khăn): \(\pi .{\left( {\frac{{35}}{2}} \right)^2} - \pi .{\left( {7,5} \right)^2} = 250\pi \) (cm2)
Diện tích vải cần để may: \(225\pi + 250\pi = 475\pi \)(cm2).
Vì tỉ lệ vải khâu (may) hao (tốn) khi may nón là \[15\% \]nên diện tích vải thực tế cần dùng là:
\(475\pi + 15\% .475\pi = 546,25\pi \approx 546,25.3,14 = 1715,225\) (cm2).
Lời giải
Trường hợp 1. Nếu thiết kế bao bì dạng hình trụ.
Ta gọi, \(R\): bán kính hình trụ; \(l\): chiều cao hình trụ
Thể tích của hình trụ là: \(V\, = \,\pi {R^2}l\, = \,100\,\left( {{\rm{ml}}} \right)\)
Diện tích toàn phần của hình trụ là: \({S_{tp}}\, = \,2\pi Rl\, + \,2\pi {R^2}\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\)
Áp dụng bất đẳng thức Cauchy cho ba số không âm: \(\pi Rl\,;\,\,\pi Rl\,;\,\,2\pi {R^2}\) ta được
\({S_{tp}}\,\, = \,\pi Rl\, + \,\pi Rl\, + \,2\pi {R^2}\, \ge \,3\sqrt[3]{{\pi Rl\,.\,\pi Rl\,.2\pi {R^2}}}\,\, = \,3\sqrt[3]{{2\pi \,\,.{{\left( {\pi {R^2}l} \right)}^2}}}\,\)
\({S_{tp}} \ge \,\,3\sqrt[3]{{2\pi \,.\,{{100}^2}}}\, \approx \,119,27\) \(\left( 1 \right)\)
Dấu \('' = ''\) xảy ra khi \(\pi Rl\, = \,\pi Rl\, = \,2\pi {R^2}\,\, \Leftrightarrow \,\,l\, = \,2R\)
Trường hợp 2. Nếu thiết kế bao bì dạng hình hộp chữ nhật có đáy là hình vuông
Ta gọi, \(a\) là độ dài cạnh đáy của hình hộp chữ nhật; \(h\)là chiều cao của hình hộp chữ nhật.
Thể tích của hình hộp chữ nhật là: \(V\,\, = \,{a^2}.h\, = \,100\,\;{\rm{ml}}\)
Diện tích toàn phần của hình hộp chữ nhật là: \({S_{tp}}\, = \,2{a^2}\, + \,4ah\, = \,2{a^2}\, + \,2ah\, + \,2ah\)
Áp dụng b.đ.t Cô-Si cho ba số không âm :\(2{a^2}\,;\,2ah\,;\,2ah\)ta được:
\({S_{tp}}\, = \,2{a^2}\, + \,2ah\, + \,2ah\,\, \ge \,3\sqrt[2]{{2{a^2}.2ah\,.\,2ah}}\, = \,3\sqrt[3]{{8{a^2}h.{a^2}h}}\)
\({S_{tp}}\, \ge \,3.2.\,\sqrt[3]{{{{100}^2}}}\, \approx \,\,129,27\,\,\,\,\,\,\,\)\(\left( 2 \right)\)
Từ (1) và (2) suy ra, thiết kế hộp sữa dạng hình trụ có chiều cao gấp 2 lần bán kính đáy thì tốn ít nguyên vật liệu nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.