Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Gia Lai năm học 2025-2026 có đáp án

a)   Với \(x \ge 0;\;x \ne 1\) thì ta có

\(\frac{{x - 1}}{{\sqrt x  - 1}} = \frac{{{{\left( {\sqrt x } \right)}^2} - {1^2}}}{{\sqrt x  - 1}} = \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\sqrt x  - 1}} = \sqrt x  + 1\)

và \(\frac{{x + \sqrt x }}{{\sqrt x  + 1}} = \frac{{{{\left( {\sqrt x } \right)}^2} + \sqrt x }}{{\sqrt x  + 1}} = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\sqrt x  + 1}} = \sqrt x \).

Vậy \(A = \sqrt x  + 1 + \sqrt x  = 2\sqrt x  + 1\).

b)  Với \(x = \sqrt[3]{{27}} - \sqrt 4  = \sqrt[3]{{{3^3}}} - \sqrt {{2^2}}  = 3 - 2 = 1\) thì không thỏa mãn điều kiện \(x \ne 1\) nên khi đó \(A\) vô nghĩa.

                a) Phương trình \(2{x^2} + 11x + 7 = 0\) có các hệ số \(a = 2,\;b = 11,\;c = 7\).

\(\Delta  = {11^2} - 4.2.7 = 65 > 0\).

                Do \(\Delta  > 0\) nên phương trình đã cho có hai nghiệm phân biệt.

                b) Theo định lí Viète, ta có \({x_1} + {x_2} =  - \frac{{11}}{2}\) và \({x_1}{x_2} = \frac{7}{2}\).

                Ta có \(T = {\left( { - \frac{{11}}{2}} \right)^2} + \frac{7}{2} = \frac{{121}}{4} + \frac{{14}}{4} = \frac{{135}}{4}\).

Ta kí hiệu \(\left\{ \begin{array}{l}2x + y = 5\;\;\;\quad \left( 1 \right)\\x - 3y =  - 1\;\quad \left( 2 \right)\end{array} \right.\).

Từ phương trình \(\left( 2 \right)\), ta có:                                                                                                           \(x = 3y - 1\quad \left( 3 \right)\)

Thế vào phương trình \(\left( 1 \right)\), ta được: \(2\left( {3y - 1} \right) + y = 5\)

                                                                                         \(6y - 2 + y = 5\)

                                                                                           \(7y = 7\)

                                                                                             \(y = 1\)

Thay \(y = 1\) vào phương trình \(\left( 3 \right)\), ta có:                                                                                                                                 \(x = 3.1 - 1 = 2\).

Vậy hệ phương trình đã cho có nghiệm duy nhất \(\left( {x\;;\;y} \right) = \left( {2\;;\;1} \right)\).

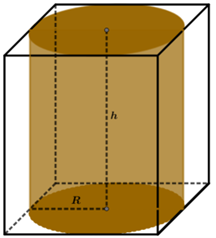
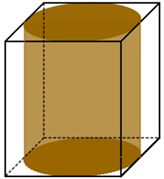
Gọi \(R\;\left( {cm} \right),\;h\;\left( {cm} \right)\) lần lượt là bán kính đáy và chiều cao của bình nước (\(R > 0,\;h > 0\)).

Khi đó chiều dài, chiều rộng, chiều cao của hộp giấy lần lượt là \(2R,\;2R,\;h\).

Thể tích của bình nước được tính theo công thức \({V_b} = \pi {R^2}h\).

Thể tích của hộp giấy được tính theo công thức \({V_h} = 2R.2R.h = 4{R^2}h\).

Theo giả thiết, ta có \({V_b} = 2000\) nên \(\pi {R^2}h = 2000\) suy ra \({R^2}h = \frac{{2000}}{\pi }\).

Vậy thể tích của hộp giấy là \({V_h} = 4.\frac{{2000}}{\pi } \approx 2546\;\left( {c{m^3}} \right)\).

Kích thước mẫu là \(N = 2 + 2 + 4 + m + m + 2 + m + 1 + 3 + 1 = 3m + 15\).

Theo giả thiết \(N = 45\) nên \(3m + 15 = 45\).

Do đó \(m = 10\).

Số kết quả có thể xảy ra của phép thử “chọn ngẫu nhiên 1 học sinh lớp 9A” là \(45\).

Số kết quả thuận lợi cho biến cố “chọn được học sinh có điểm kiểm tra cuối kì 2 môn Toán lớn hơn 7” là \(m + 1 + 3 + 1 = m + 5 = 10 + 5 = 15\).

Xác suất cần tính là \(\frac{{15}}{{45}} = \frac{1}{3}\).