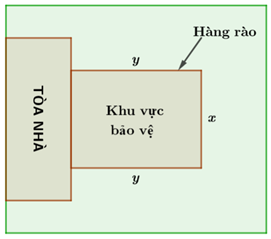
Người ta cần lập hàng rào quanh khu vực bảo vệ có dạng hình chữ nhật cho một tòa nhà (hình vẽ bên). Hỏi nếu có \(100\) mét hàng rào bao quanh ba mặt như trên thì diện tích tối đa của khu vực bảo vệ là bao nhiêu?

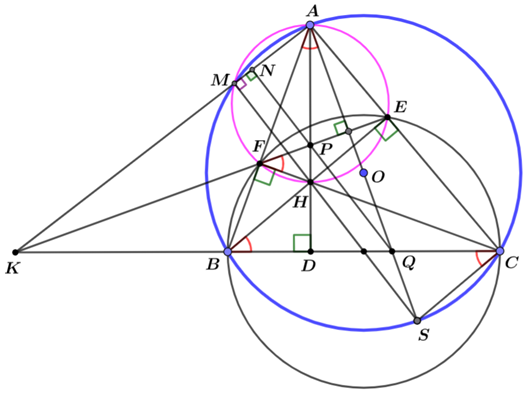
a)   Vì \(BE\), \(CF\) là các đường cao của \(\Delta ABC\) nên \(\Delta BCE\) vuông tại \(E\) và \(\Delta BCF\) vuông tại \(F\).

Do đó, \(\Delta BCE\) và \(\Delta BCF\) nội tiếp đường tròn đường kính \(BC\). Do đó tứ giác \(BCEF\) nội tiếp đường tròn đường kính \(BC\).

b)   Xét hai tam giác \(KBE\) và \(KFC\), ta có:

                     +) \(\widehat {EKB} = \widehat {CKF}\) (góc chung)

                     +) \(\widehat {KEB} = \widehat {KCF}\) (hai góc nội tiếp cùng chắn  của đường tròn đường kính \(BC\))

Suy ra \(\Delta KBE \sim \Delta KFC\).

Do đó \(\frac{{KE}}{{KC}} = \frac{{KB}}{{KF}}\).

Suy ra \(KE.KF = KB.KC\) (đpcm).

c)   Ta có: \(\widehat {BEC} = \widehat {SCA} = 90^\circ \) (vì \(BE\) là đường cao của \(\Delta ABC\) và \(\widehat {SCA}\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\))

Suy ra \(BH\;{\rm{//}}\;SC\).

Ta có:

                     +) \(\widehat {BAS} = \widehat {BCS}\) (hai góc nội tiếp cùng chắn  của đường tròn \(\left( O \right)\))

                     +) \(\widehat {BCS} = \widehat {CBE}\) (do \(BH\;{\rm{//}}\;SC\))

                     +) \(\widehat {CBE} = \widehat {CFE}\) (hai góc nội tiếp cùng chắn  của đường tròn đường kính \(BC\))

Suy ra \(\widehat {BAS} = \widehat {CFE} \Rightarrow \widehat {AFP} + \widehat {BAS} = \widehat {AFP} + \widehat {CFE} = \widehat {AFH} = 90^\circ \).

Suy ra \(KP \bot AQ\).

Mà \(AP \bot KQ\) (do \(AH \bot BC\)) nên \(P\) là trực tâm \(\Delta AKQ\).

Suy ra \(PQ \bot AK\quad \left( 1 \right)\).                 

Gọi \(M\) là giao điểm của \(AK\) và \(\left( O \right)\) (với \(M \ne A\)).

Chứng minh tương tự câu b), ta có \(KM.KA = KB.KC\). Suy ra \(KE.KF = KM.KA\).

Suy ra tứ giác \(AMFE\) nội tiếp đường tròn đường kính \(AH\).

Suy \(\widehat {AMH} = 90^\circ \).

Mà \(\widehat {AMS} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)\))

nên \(M,\;H,\;S\) thẳng hàng. Suy ra \(HS \bot AK\quad \left( 2 \right)\).

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(QP\) song song với \(HS\).

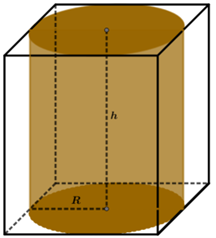
Gọi \(R\;\left( {cm} \right),\;h\;\left( {cm} \right)\) lần lượt là bán kính đáy và chiều cao của bình nước (\(R > 0,\;h > 0\)).

Khi đó chiều dài, chiều rộng, chiều cao của hộp giấy lần lượt là \(2R,\;2R,\;h\).

Thể tích của bình nước được tính theo công thức \({V_b} = \pi {R^2}h\).

Thể tích của hộp giấy được tính theo công thức \({V_h} = 2R.2R.h = 4{R^2}h\).

Theo giả thiết, ta có \({V_b} = 2000\) nên \(\pi {R^2}h = 2000\) suy ra \({R^2}h = \frac{{2000}}{\pi }\).

Vậy thể tích của hộp giấy là \({V_h} = 4.\frac{{2000}}{\pi } \approx 2546\;\left( {c{m^3}} \right)\).