Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 34

a) \[\Omega  = \left\{ {10\;;\,\,11\;;\;\,12\;;\;\,13\;;\;\,...\;;\,\;98\;;\;\,99} \right\}\]

b) Kết quả thuận lợi cho biến cố \(B:\) “Số tự nhiên được viết ra chia hết cho \[11\]” là:

\[11\;;\,\,22\;;\,\,33\;;\;\,44\;;\;\,55\;;\;\,66\;;\;\,77\;;\;\,88\;;\;\,99\]

c) Kết quả thuận lợi cho biến cố \(C\): “Số tự nhiên được viết ra chia cho \[10\] dư \[6\]” là:

\[16\;;\;26\;;\;\,36\;;\;\,46\;;\;\,56\;;\;\,76\;;\;\,86\;;\;\,96\]

a) Thay \(x = 9\) (thỏa mãn điều kiện xác định) vào biểu thức \[A\] ta có:

\(A = \frac{{\sqrt 9  + 4}}{{\sqrt 9  - 1}} = \frac{7}{2}\)

            Vậy khi \(x = 9\) thì \(A = \frac{7}{2}\).

b) \(B = \frac{{3\sqrt x  + 1}}{{x + 2\sqrt x  - 3}} - \frac{2}{{\sqrt x  + 3}}\)

              \(B = \frac{{3\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} - \frac{2}{{\sqrt x  + 3}}\)

\(B = \frac{{3\sqrt x  + 1 - 2\sqrt x  + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\)

              \(B = \frac{{\sqrt x  + 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\)

\(B = \frac{1}{{\sqrt x  - 1}}\)

            Vậy \(B = \frac{1}{{\sqrt x  - 1}}\) với \(x \ge 0\); \(x \ne 1\).

            c) \(\frac{A}{B} = \frac{{\sqrt x  + 4}}{{\sqrt x  - 1}}:\frac{1}{{\sqrt x  - 1}} = \sqrt x  + 4\,\,\,\left( {x \ge 0;x \ne 1;x \ne 3} \right)\)

\(\begin{array}{l}\frac{A}{B} \ge \frac{x}{4} + 5\\\sqrt x  + 4 \ge \frac{x}{4} + 5\\\frac{x}{4} - \sqrt x  + 1 \le 0\end{array}\)

\(\begin{array}{l}x - 4\sqrt x  + 4 \le 0\\{\left( {\sqrt x  - 2} \right)^2} \le 0\end{array}\)

            Mà \({\left( {\sqrt x  - 2} \right)^2} \ge 0\) với mọi \[x\] thỏa mãn điều kiện xác định.

              \(\begin{array}{l}{\left( {\sqrt x  - 2} \right)^2} \le 0\\\sqrt x  - 2 = 0\\\sqrt x  = 2\\x = 4\end{array}\).

            So với điều kiện, thỏa mãn.

            Vậy \(x = 4\) thì \(\frac{A}{B} \ge \frac{x}{4} + 5\).

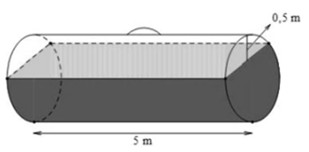
Ta có: \(HO = OC - CH = 1 - \frac{1}{2} = \frac{1}{2}\) \({\rm{(m)}}\)

Ta có: \(HB = \sqrt {O{B^2} - O{H^2}}  = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}}  = \frac{{\sqrt 3 }}{2}\)

\(AB = 2HB = \sqrt 3 \) \({\rm{(m)}}\)

Ta có: \({S_{OAB}} = \frac{1}{2}AB\,.\,OH = \frac{1}{2}\,\,.\,\,\sqrt 3 \,\,.\,\,\frac{1}{2} = \frac{{\sqrt 3 }}{4}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Tam giác \(OHB\) có \(\sin \widehat {HOB} = \frac{{HB}}{{OB}} = \frac{{\sqrt 3 }}{2}\)

\(\widehat {HOB} = {60^0}\)

\(\widehat {AOB} = 2\widehat {HOB} = {120^0}\)

Gọi \({S_1}\) là diện tích hình quạt tròn \(OACB\), ta có:

\({S_1} = \frac{{\pi {R^2}120}}{{360}} = \frac{\pi }{3}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Gọi \({S_2}\) là diện tích hình viên phân giới hạn bởi dây \(AB\) và cung nhỏ , ta có:

\({S_2} = {S_1} - {S_{OAB}} = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi  - 3\sqrt 3 }}{{12}}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Thể tích phần dầu đã hút đi là: \({V_1} = \frac{1}{3}\,{S_2}.\,\,5 = \frac{{5.\,\,\left( {4\pi  - 3\sqrt 3 } \right)}}{{36}}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Thể tích của thùng dầu là: \(V = \frac{1}{3}\pi {R^2}.\,\,5 = \frac{{5\pi }}{3}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Thể tích dầu còn lại trong thùng là: \[{V_2} = V - {V_1} = \frac{{5\pi }}{3} - \frac{{5\,\,.\,\,\left( {4\pi  - 3\sqrt 3 } \right)}}{{36}} \approx 4,21\]\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)

Vậy thể tích dầu còn lại trong thùng là \(4,21\,\,{{\rm{m}}^{\rm{3}}}\).

Đổi  \(0,5\,{\rm{kg}} = 5{\rm{00}}\,{\rm{g}}\)

            Gọi khối lượng dung dịch acid có nồng độ \[10\% \] đem trộn là \[x\]\[\left( {\rm{g}} \right)\]\[\left( {0 < x < 500} \right)\].

            Gọi khối lượng dung dịch acid có nồng độ \(20\% \) đem trộn là \[y\]\[\left( {\rm{g}} \right)\]\[\left( {0 < y < 500} \right)\].

            Vì trộn \[x\]\[\left( {\rm{g}} \right)\] dung dịch acid có nồng độ \[10\% \] và \[y\]\[\left( {\rm{g}} \right)\] dung dịch acid loại có nồng độ \(20\% \) để được \(500\)\({\rm{kg}}\) acid  mới nên ta có phương trình:  \[x + y = 500\]   (1)

            Vì trộn  hai loại dung dịch acid cùng loại có nồng độ acid lần lượt là \[10{\raise0.5ex\hbox{$\scriptstyle 0$}

\kern-0.1em/\kern-0.15em

\lower0.25ex\hbox{$\scriptstyle 0$}}\] và \(20\% \) để được \(0,5\)\({\rm{kg}}\) dung dịch có nồng độ acid là  \(16\% \)nên ta có phương trình:

\[10\% x + 20\% y = 16\% \,\,.\,\,500\]

\[0,1x + 0,2y = 80\]    (2)

            Từ (1) và (2) ta có hệ phương trình:

            \[\left\{ {\begin{array}{*{20}{c}}{0,1x + 0,2y = 80\,\,\,\,\,\,\,\left( 1 \right)}\\{x + y = 500\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\]

            Từ \[\left( 2 \right)\] suy ra \[y = 500 - x\,\,\,\,\,\,\left( 3 \right)\]

            Thay \[\left( 3 \right)\] vào  \[\left( 1 \right)\] ta được  \[0,1x + 0,2\,\left( {500 - x} \right) = 80\]

            \[0,1x + 100 - 0,2x = 80\]

            \[ - 0,1x =  - 20\]

            \[x = 200\] (nhận)

            Thay \[x = 200\] vào  \[\left( 3 \right)\] ta được  \[y = 300\,\](nhận)

            Vậy khối lượng dung dịch acid loại có nồng độ acid \[10\% \]là \[20\,0\,{\rm{g}}\].

                   Khối lượng dung dịch acid loại có nồng độ acid \(20\% \)là \[300\,{\rm{g}}\].

- Gọi vận tốc của xe máy thứ nhất và xe máy thứ hai lần lượt là \({\rm{x}}\,{\rm{,}}\,\,{\rm{y}}\,\,\left( {{\rm{km/h}}} \right)\,\), \({\rm{x}}\,{\rm{ > }}\,3\), \({\rm{y > }}\,0\).

- Vì xe thứ nhất đi nhanh hơn xe thứ hai là \(3\,\,{\rm{km/h}}\) nên ta có: \(x\, - \,y\, = \,3\,\,\,\,\,\,\,\,\left( 1 \right)\)

- Trong \(3\) giờ \(20\) phút  = \(\frac{{10}}{3}\,\,{\rm{h}}\), xe máy thứ nhất đi được : \(\frac{{10}}{3}x\,\,\left( {{\rm{km}}} \right)\)

- Trong \(3\) giờ \(40\) phút  = \(\frac{{11}}{3}\,\,{\rm{h}}\), xe máy thứ hai đi được : \(\frac{{11}}{3}{\rm{y}}\,\,\left( {{\rm{km}}} \right)\)

- Đó là quãng đường từ Hà Nội đến Nam Định nên ta có phương trình:

            \(\begin{array}{l}\frac{{10}}{3}x\,\, = \frac{{11}}{3}y\\\frac{{10}}{3}x\,\, - \frac{{11}}{3}y\,\, = \,\,0\,\,\,\,\,\,\,\,\,{\rm{ }}\left( 2 \right)\end{array}\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:

Vậy vận tốc của xe máy thứ nhất là \(33\,\,\left( {{\rm{km/h}}} \right)\) và vận tốc xe máy thứ hai \(30\,\,\left( {{\rm{km/h}}} \right)\)

            Quãng đường từ Hà Nội đến Nam Định là: \(\frac{{10}}{3}\,\,.\,\,33 = 110\,\,\left( {{\rm{km}}} \right)\).