(0,5 điểm) Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là \(5\,{\rm{m}}\), có bán kính đáy \[{\rm{1}}\,{\rm{m}}\], với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với \[0,5\,{\rm{m}}\] của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy \[\pi {\rm{ }} \approx {\rm{ }}3,14\], kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị \[{{\rm{m}}^{\rm{3}}}\]) .
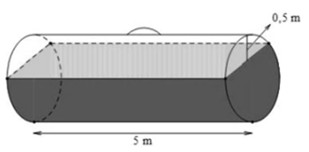
(0,5 điểm) Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là \(5\,{\rm{m}}\), có bán kính đáy \[{\rm{1}}\,{\rm{m}}\], với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với \[0,5\,{\rm{m}}\] của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy \[\pi {\rm{ }} \approx {\rm{ }}3,14\], kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị \[{{\rm{m}}^{\rm{3}}}\]) .
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 34 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(HO = OC - CH = 1 - \frac{1}{2} = \frac{1}{2}\) \({\rm{(m)}}\)
Ta có: \(HB = \sqrt {O{B^2} - O{H^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
\(AB = 2HB = \sqrt 3 \) \({\rm{(m)}}\)
Ta có: \({S_{OAB}} = \frac{1}{2}AB\,.\,OH = \frac{1}{2}\,\,.\,\,\sqrt 3 \,\,.\,\,\frac{1}{2} = \frac{{\sqrt 3 }}{4}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Tam giác \(OHB\) có \(\sin \widehat {HOB} = \frac{{HB}}{{OB}} = \frac{{\sqrt 3 }}{2}\)
\(\widehat {HOB} = {60^0}\)
\(\widehat {AOB} = 2\widehat {HOB} = {120^0}\)
Gọi \({S_1}\) là diện tích hình quạt tròn \(OACB\), ta có:
\({S_1} = \frac{{\pi {R^2}120}}{{360}} = \frac{\pi }{3}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Gọi \({S_2}\) là diện tích hình viên phân giới hạn bởi dây \(AB\) và cung nhỏ , ta có:
\({S_2} = {S_1} - {S_{OAB}} = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi - 3\sqrt 3 }}{{12}}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Thể tích phần dầu đã hút đi là: \({V_1} = \frac{1}{3}\,{S_2}.\,\,5 = \frac{{5.\,\,\left( {4\pi - 3\sqrt 3 } \right)}}{{36}}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Thể tích của thùng dầu là: \(V = \frac{1}{3}\pi {R^2}.\,\,5 = \frac{{5\pi }}{3}\)\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Thể tích dầu còn lại trong thùng là: \[{V_2} = V - {V_1} = \frac{{5\pi }}{3} - \frac{{5\,\,.\,\,\left( {4\pi - 3\sqrt 3 } \right)}}{{36}} \approx 4,21\]\({\rm{(}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Vậy thể tích dầu còn lại trong thùng là \(4,21\,\,{{\rm{m}}^{\rm{3}}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Thể tích của quả dưa hấu hình vuông là:
\({V_1} = {18^3} = 5832\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của một miếng dưa hấu nhỏ hình vuông có cạnh \(5\)cm là:
\({V_2} = {5^3} = 125\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Số miếng dưa nhỏ được cắt ra là: \(5832\,:\,125 = 46,656\) ( miếng)
Số đĩa dưa mà bạn Minh có thể xếp được là: \(46,656\,:\,12 \approx 4\) (đĩa).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi \(0,5\,{\rm{kg}} = 5{\rm{00}}\,{\rm{g}}\)
Gọi khối lượng dung dịch acid có nồng độ \[10\% \] đem trộn là \[x\]\[\left( {\rm{g}} \right)\]\[\left( {0 < x < 500} \right)\].
Gọi khối lượng dung dịch acid có nồng độ \(20\% \) đem trộn là \[y\]\[\left( {\rm{g}} \right)\]\[\left( {0 < y < 500} \right)\].
Vì trộn \[x\]\[\left( {\rm{g}} \right)\] dung dịch acid có nồng độ \[10\% \] và \[y\]\[\left( {\rm{g}} \right)\] dung dịch acid loại có nồng độ \(20\% \) để được \(500\)\({\rm{kg}}\) acid mới nên ta có phương trình: \[x + y = 500\] (1)
Vì trộn hai loại dung dịch acid cùng loại có nồng độ acid lần lượt là \[10{\raise0.5ex\hbox{$\scriptstyle 0$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 0$}}\] và \(20\% \) để được \(0,5\)\({\rm{kg}}\) dung dịch có nồng độ acid là \(16\% \)nên ta có phương trình:
\[10\% x + 20\% y = 16\% \,\,.\,\,500\]
\[0,1x + 0,2y = 80\] (2)
Từ (1) và (2) ta có hệ phương trình:
\[\left\{ {\begin{array}{*{20}{c}}{0,1x + 0,2y = 80\,\,\,\,\,\,\,\left( 1 \right)}\\{x + y = 500\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\]
Từ \[\left( 2 \right)\] suy ra \[y = 500 - x\,\,\,\,\,\,\left( 3 \right)\]
Thay \[\left( 3 \right)\] vào \[\left( 1 \right)\] ta được \[0,1x + 0,2\,\left( {500 - x} \right) = 80\]
\[0,1x + 100 - 0,2x = 80\]
\[ - 0,1x = - 20\]
\[x = 200\] (nhận)
Thay \[x = 200\] vào \[\left( 3 \right)\] ta được \[y = 300\,\](nhận)
Vậy khối lượng dung dịch acid loại có nồng độ acid \[10\% \]là \[20\,0\,{\rm{g}}\].
Khối lượng dung dịch acid loại có nồng độ acid \(20\% \)là \[300\,{\rm{g}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập