Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Thanh Hóa có đáp án
51 người thi tuần này 4.6 97 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1.\[\begin{array}{l}P = \frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{{\sqrt x + 1}}{{\sqrt x - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}\\\,\,\,\,\, = \frac{{\sqrt x (\sqrt x - 2) + (\sqrt x + 1)(\sqrt x + 2) - 2 - 5\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}\\\end{array}\]
\[\begin{array}{l}\,\,\,\,\,\,\,\, = \,\,\frac{{x - 2\sqrt x + x + 3\sqrt x + 2 - 2 - 5\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}\,\,\,\,\, = \,\,\,\,\frac{{2x - 4\sqrt x }}{{(\sqrt x - 2)(\sqrt x + 2)}}\\\,\,\,\,\,\,\,\, = \,\,\frac{{2\sqrt x (\sqrt x - 2)}}{{(\sqrt x - 2)(\sqrt x + 2)}}\,\,\,\,\, = \frac{{2\sqrt x }}{{\sqrt x + 2}}\end{array}\]
Vậy P = \[ = \frac{{2\sqrt x }}{{\sqrt x + 2}}\] với \(x \ge 0\) và \(x \ne 4\)
2.Theo ý (1) ta có P \[ = \frac{{2\sqrt x }}{{\sqrt x + 2}}\] với \(x \ge 0\) và \(x \ne 4\)
\(P > 1\) hay \[\frac{{2\sqrt x }}{{\sqrt x + 2}}\] > 1 \( \Rightarrow 2\sqrt x > \sqrt x + 2\) ( vì \(\sqrt x + 2 > 0\) với \(x \ge 0\) )
\( \Rightarrow 2\sqrt x - \sqrt x > 2 \Rightarrow \sqrt x > 2 \Rightarrow x > 4\)
Vậy \(x > 4\)thì \(P > 1\)
Lời giải
1. Đường thằng \(\left( d \right):y = ax + b\) có hệ số góc là \(3\) nên \(a = 3\)
Khi đó: \(\left( d \right):y = 3x + b\) đi qua \(M\left( { - 1;2} \right)\) nên thay \(x = - 1;y = 2\) ta được: \(2 = 3.\left( { - 1} \right) + b \Leftrightarrow b = 5\)
Vậy \(a = 3;b = 5\)
2. \(\left\{ \begin{array}{l}3x + y = 6\\x - y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\x - y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\1 - y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là \((x;y) = (1;3)\)
Lời giải
1. Theo bài ra ta có: \(a = 1;b = - 3;c = 2\)
Ta lại có: \[a + b + c = 1 + \left( { - 3} \right) + 2 = 0\]
nên phương trình có hai nghiệm: \[{x_1} = 1\]và \[{x_2} = \frac{c}{a} = \frac{2}{1} = 2\]
Vậy tập nghiệm của phương trình là \[S = \left\{ {1;2} \right\}\]
2.
\({x^2} - 2mx - {m^2} - 2 = 0\)
Vì \(\,a = 1 \ne 0\,\)và \(ac = {m^{^2}} - 2 < 0\)
Nên phương trình có 2 nghiệm trái dấu với mọi \(m\)
Mà \({x_1} < {x_2}\) nên \({x_1} < 0 < {x_2}\) suy ra\(\left| {{x_1}} \right| = - {x_1};\left| {{x_2}} \right| = {x_2}\)
Khi đó theo định lí vi- ét ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\,\,\,\,\,\,\,\,\,\\{x_1}.{x_2} = - {m^2} - 2\,(3)\,\,\end{array} \right.\]
Thay vào đề ra ta có: \({x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\)
\({x_2} + 2{x_1} - 3{x_1}{x_2} = 3{m^2} + 3m + 4\)
\( \Rightarrow {x_2} + 2{x_1} = 3m - 2\)
\[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\,\,\,\,\,\,\,\,\,(1)\\{x_1} + 2{x_2} = 3m - 2\,\,\,(2)\end{array} \right.\]
Lấy (1) – (2) Suy ra \({x_1} = m - 2;{x_2} = m + 2\)
Thay vào (3) Ta đươc: \({m^2} - 4 = - {m^2} - 2\) \[ \Leftrightarrow m = \pm 1\]
Vậy \(m = \pm 1\)
Lời giải
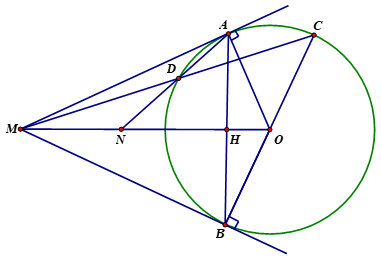
1. Vì \(MA\) và \(MB\) là hai tiếp tuyến của đường tròn \(\left( O \right)\)
Nên \(\widehat {MAO} = {90^0}\) và \(\widehat {MBO} = {90^0}\)
Xét tứ giác\(MAOB\)có : \(\widehat {MAO} + \widehat {MBO} = {90^0} + {90^0} = {180^0}\). Hai góc này đối nhau
Suy ra tứ giác \(MAOB\) nội tiếp
2. Nhận thấy \(MN//AC\) (vì cùng vuông góc với \(AH\))
Do đó \[\widehat {DMN} = \widehat {ACM}\] (so le trong)
Mà \(\widehat {MAD} = \widehat {ACM}\) (cùng chắn cung \(AD\))
Suy ra \(\widehat {DMN} = \widehat {MAD}\)
Xét \(\Delta MND\) và \(\Delta ANM\) có:
\(\widehat N\) là góc chung
\(\widehat {DMN} = \widehat {MAN} = \widehat {MAD}\)
Suy ra \(\Delta MND\) \( \sim \) \(\Delta ANM\)(g.g)
\( \Rightarrow \frac{{MN}}{{ND}} = \frac{{NA}}{{MN}}\) \( \Rightarrow M{N^2} = ND.NA\)
1. Dễ thấy \(M{A^2} = MD.MC\)
và \(M{A^2} = MH.MO\) (hệ thức về cạnh và đường cao trong tam giác vuông \(MAO\))
Do đó \(MD.MC = MH.MO\)
Suy ra tứ giác \(CDHO\) nội tiếp được đường tròn.
\( \Rightarrow \widehat {MCO} = \widehat {MHD}\)
\( \Rightarrow \Delta MDH\, \sim \Delta MOC\,\,\left( {g.g} \right)\)
\( \Rightarrow \widehat {MHD} = \widehat {MCO}\)
Mà \(\widehat {MCO} = \widehat {DAH}\) (cùng chắn cung \(DB\))
nên \[\widehat {MHD} = \widehat {DAH}\]
Lại có \(\widehat {MHD} + \widehat {DHA} = {90^0}\) nên \(\widehat {DAH} + \widehat {DHA} = {90^0}\)
Suy ra \(DH \bot NA\)
Suy ra \(H{N^2} = ND.NA\)
Lại có \(M{N^2} = ND.NA\) nên \(H{N^2} = M{N^2} = > HN = MN\)
Ta có \(\frac{{H{A^2}}}{{H{D^2}}} = \frac{{AD.AN}}{{AD.DN}} = \frac{{AN}}{{DN}}\) và \(\frac{{AC}}{{HN}} = \frac{{AC}}{{HM}} = \frac{{AD}}{{DN}}\)
Suy ra \({\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = \frac{{AN}}{{DN}} - \frac{{AD}}{{DN}} = \frac{{DN}}{{DN}} = 1\)
Lời giải
Ta chứng minh bổ đề: \(\frac{1}{{{m^2}}} + \frac{1}{{{n^2}}} \ge \frac{8}{{{{(m + n)}^2}}}\)
Áp dụng BĐT Cô si: \(\frac{1}{{{m^2}}} + \frac{1}{{{n^2}}} \ge 2\sqrt {\frac{1}{{{m^2}{n^2}}}} = \frac{2}{{mn}}.\,\,\)
\(Do\,\,mn \le \frac{{{{(m + n)}^2}}}{4}\) Nên suy ra \(\frac{1}{{{m^2}}} + \frac{1}{{{n^2}}} \ge \frac{8}{{{{(m + n)}^2}}}\)
Ta có:
\[\begin{array}{l}4{{\rm{x}}^2} + 4 \ge 2\sqrt {4{{\rm{x}}^2}.4} = 8{\rm{x}}\\4{y^2} + 4 \ge 8y\\4{z^2} + 4 \ge 8{\rm{z}}\end{array}\]
Cộng vế với vế ta được: \(24 \ge 8x + 8z + 2y \Leftrightarrow 3 \ge {\rm{x}} + {\rm{z}} + \frac{y}{4}\)
Ta lại có:
\(\frac{1}{{{{(z + 1)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{8}{{{{(x + 3)}^2}}} = \frac{1}{{{{(z + 1)}^2}}} + \frac{1}{{{{\left( {\frac{y}{4} + 1} \right)}^2}}} + \frac{8}{{{{(x + 3)}^2}}} \ge \frac{8}{{{{\left( {z + \frac{y}{4} + 2} \right)}^2}}} + \frac{8}{{{{(x + 3)}^2}}} \ge \)
\( \ge 8.\frac{8}{{{{\left( {z + \frac{y}{4} + 2 + x + 3} \right)}^2}}} \ge 8.\frac{8}{{{{(3 + 2 + 3)}^2}}} = 1\)
\(\frac{1}{{{{(z + 1)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{8}{{{{(x + 3)}^2}}} + 2023 \ge 1 + 2023 = 2024\)
Dấu “=” xảy ra khi \(x = 1;y = 4;z = 1\)