Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Phú Yên có đáp án
46 người thi tuần này 4.6 90 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) a) Rút gọn, tính giá trị A=\(\left( {\frac{{x + 2}}{{x\sqrt x - 1}} + \frac{{\sqrt x }}{{x + \sqrt x + 1}} + \frac{1}{{1 - \sqrt x }}} \right):\frac{{\;\sqrt x - 1}}{{\sqrt x + 1}}\)
Biết \({\rm{x}} = \frac{{6 + 2\sqrt 5 }}{{2 + \sqrt {6 + 2\sqrt 5 } }} + \frac{{6 - 2\sqrt 5 }}{{2 - \sqrt {6 - 2\sqrt 5 } }}\).
-Rút gọn \({\rm{A}}\): Với điều kiện \({\rm{x}} \ge 0,{\rm{x}} \ne 1\), ta có:
\({\rm{A}} = \frac{{{\rm{x}} + 2 + \sqrt {\rm{x}} \left( {\sqrt {\rm{x}} - 1} \right) - \left( {{\rm{x}} + \sqrt {\rm{x}} + 1} \right)}}{{{\rm{x}}\sqrt {\rm{x}} - 1}}:\frac{{\sqrt {\rm{x}} - 1}}{{\sqrt {\rm{x}} + 1}} = \frac{{{{\left( {\sqrt {\rm{x}} - 1} \right)}^2}}}{{{\rm{x}}\sqrt {\rm{x}} - 1}} \times \frac{{\sqrt {\rm{x}} + 1}}{{\sqrt {\rm{x}} - 1}} = \frac{{\sqrt {\rm{x}} + 1}}{{{\rm{x}} + \sqrt {\rm{x}} + 1}}\).
-Lại có: \({\rm{x}} = \frac{{6 + 2\sqrt 5 }}{{2 + \sqrt {6 + 2\sqrt 5 } }} + \frac{{6 - 2\sqrt 5 }}{{2 - \sqrt {6 - 2\sqrt 5 } }} = \frac{{6 + 2\sqrt 5 }}{{2 + \sqrt 5 + 1}} + \frac{{6 - 2\sqrt 5 }}{{2 - \sqrt 5 + 1}} = \frac{{16}}{4} = 4\).
Do đó: \({\rm{A}} = \frac{{\sqrt 4 + 1}}{{4 + \sqrt 4 + 1}} = \frac{3}{7}\)
b) Biết \(\frac{1}{{\rm{a}}} + \frac{1}{{\rm{b}}} = \sqrt 2 \)(a>1,b>1).CMR:ab-\(\sqrt {1 - {{\rm{a}}^2}{{\rm{b}}^2} + {{\rm{a}}^2} + {{\rm{b}}^2}} = 1\)
Vì \({\rm{a}} > 1,{\rm{b}} > 1\) nên: \(\frac{1}{{\rm{a}}} + \frac{1}{{\rm{b}}} = \sqrt 2 \Leftrightarrow {{\rm{a}}^2} + {{\rm{b}}^2} = 2{{\rm{a}}^2}{{\rm{b}}^2} - 2{\rm{ab}}\) .
Khi đó: \({\rm{B}} = ab - \sqrt {1 - {a^2}{b^2} + 2{a^2}{b^2} - 2ab} = ab - \sqrt {{{\left( {{\rm{ab}} - 1} \right)}^2}} \).
Vì \({\rm{a}} > 1,{\rm{b}} > 1 \Rightarrow {\rm{ab}} > {\rm{n\^e n\;B}} = {\rm{ab}} - {\rm{ab}} + 1 = 1\) (điều phải chứng minh)
Lời giải
a)Giải các phương trình, hệ phương trình
\(a){\left( {x - \sqrt 3 } \right)^3} + {\left( {x + \sqrt 5 } \right)^3}\)+\({\left( {\sqrt 3 - \sqrt 5 - 2x} \right)^3}\)=0
Đặt \({\rm{u}} = {\rm{x}} - \sqrt 3 ,{\rm{\;v}} = {\rm{x}} + \sqrt 5 \), khi đó \(\sqrt 3 - \sqrt 5 - 2{\rm{x}} = - \left( {{\rm{u}} + {\rm{v}}} \right)\)
PTCĐ viết lại là:\({{\rm{u}}^3} + {{\rm{v}}^3} - {\left( {{\rm{u}} + {\rm{v}}} \right)^3} = 0 \Leftrightarrow 3\left( {{\rm{u}} + {\rm{v}}} \right){\rm{uv}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u + v = 0}\\{u = 0}\\{v = 0}\end{array}} \right.\)
(1):\({\rm{u}} + {\rm{v}} = 0 \Leftrightarrow {\rm{x}} - \sqrt 3 + {\rm{x}} + \sqrt 5 = 0 \Leftrightarrow {\rm{x}} = \frac{{\sqrt 3 - \sqrt 5 }}{2}\)
(2):u = 0 \( \Leftrightarrow {\rm{x}} = \sqrt 3 \); (3):\({\rm{v}} = 0 \Leftrightarrow {\rm{x}} = - \sqrt 5 \)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\frac{{\sqrt 3 - \sqrt 5 }}{2};\sqrt 3 ;\sqrt 5 } \right.\)}
Cách 2: Đặt \({\rm{a}} = {\rm{x}} - \sqrt 3 + {\rm{x}} + \sqrt 5 \), c=\(\sqrt 3 - \sqrt 5 - 2{\rm{x}}\). Khi đó:
\({{\rm{a}}^3} + {{\rm{b}}^3} + {{\rm{c}}^3} = 3{\rm{abc}}\)( chứng minh). Từ đó ta có nghiệm như cách 1
b)\(\left\{ {\begin{array}{*{20}{c}}{{{\left( {{\rm{xy}}} \right)}^3} + 3{\rm{x}}{{\rm{y}}^3} + 2 = 6{{\rm{y}}^{2{\rm{\;\;\;\;\;}}}}\left( 1 \right)}\\{3{\rm{x}}{{\rm{y}}^3} = {{\rm{y}}^2} + 2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 2 \right)}\end{array}} \right.\)
Đặt\(\left\{ {\begin{array}{*{20}{c}}{u = xy}\\{v = {y^2}}\end{array}} \right.\) . Dễ thấy y\( \ne 0.\) Từ(2) suy ra 3\(xy = \frac{{{y^2} + 2}}{{{y^2}}} > 0,\) do đó ta luôn có u\( > 0,{\rm{v}} > 0\left( 3 \right)\)
Ta có hệ phương trình mới:\(\left\{ {\begin{array}{*{20}{c}}{{{\rm{u}}^3} + 3uv + 2 = 6v\;\left( 4 \right)}\\{3uv = v + 2\;\;\;\;\;\;\;\;\;\;\;\left( 5 \right)\;\;\;\;}\end{array}} \right.\)
Thế (5) và (4) ta được:\(v = \frac{{{{\rm{u}}^3} + 4}}{5}\) (6)
Thế (6) vào (5) ta được:
\(3{{\rm{u}}^4} - {{\rm{u}}^3} + 12{\rm{u}} - 14 = 0 \Leftrightarrow \left( {{\rm{u}} - 1} \right)(3{{\rm{u}}^3} + 2{{\rm{u}}^2}\)+\(2{\rm{u}} + 14) = 0\)(7)
Đối chiếu với điều kiện(3) thì 3\({u^3} + 2{u^2} + 2u + 14 > 0\) nên(7) có nghiệm \({\rm{u}} = 1\)
Với \({\rm{u}} = 1\), từ (6) suy ra \({\rm{v}} = 1\) hay \({{\rm{y}}^2} = 1 \Leftrightarrow {\rm{y}} = \pm 1 \Rightarrow {\rm{x}} = \pm 1{\rm{\;}}\).
Vậy hệ phương trình có 2 nghiệm: \(\left( {{\rm{x}};{\rm{y}}} \right) = \left( {1;1} \right)\) và \(\left( {{\rm{x}};{\rm{y}}} \right) = \left( { - 1; - 1} \right)\)
Lời giải
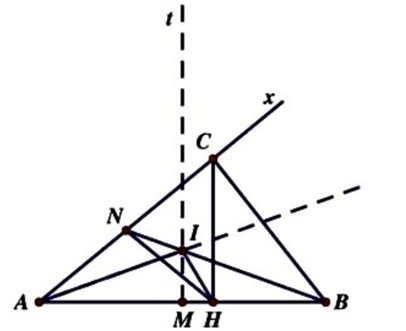
a) Chứng minh \(\Delta {\rm{NHB}}\) cân.
\(\Delta {\rm{AHC}}\) vuông tại \({\rm{H}}\) có \({\rm{HN}}\) là trung tuyến nên \({\rm{NA}} = {\rm{NC}} = {\rm{NH}}\) nên \(\Delta {\rm{HNA}}\) cân tại N, suy ra (1)..
Theo tính chất góc ngoài của tam giác thì \(\widehat {{\rm{NHA}}} = \widehat {{\rm{HNB}}} + \widehat {{\rm{HBN}}}\) (2).
Từ (1) và (2) suy ra \(\widehat {{\rm{HNB}}} = \widehat {{\rm{HBN}}}\) hay \(\Delta {\rm{NHB}}\) cân tại H.
Chứng minh \({\rm{B}}{{\rm{H}}^2} = HI.{\rm{BN}}\)
Theo a) \(\Delta {\rm{NHB\;}}\)cân tại H suy ra \(HB = HN = \frac{1}{2}\)AC (3)
Xét \(\Delta {\rm{NHI\;v\`a \;}}\Delta {\rm{BHI\;c\'o }}\)
\(\left\{ {\begin{array}{*{20}{c}}{IAN = IBH}\\{IA = IB}\\{AN = BH\left( { = HN} \right)}\end{array} \Rightarrow \Delta {\rm{ANI}} = \Delta {\rm{BHI}} \Rightarrow {\rm{IN}} = {\rm{IH}}} \right.\)
Dẫn đến \(\Delta {\rm{NIH\;c\^a n\;tai I}} \Rightarrow \widehat {IHN}{\rm{ = }}\widehat {INH} \Rightarrow \Delta {\rm{NHB}}\~\Delta {\rm{NIH}}\) (hai tam giác cân có góc ở đáy bằng nhau)
\( \Rightarrow \frac{{{\rm{BH}}}}{{{\rm{BN}}}} = \frac{{{\rm{HI}}}}{{{\rm{HN}}}} \Rightarrow {\rm{BH}}.{\rm{BN}} = {\rm{HI}}.{\rm{BN}} \Rightarrow {\rm{B}}{{\rm{H}}^2} = {\rm{HI}}.{\rm{BN}}\)
b) Tính tỉ số \(\frac{{{\rm{AB}}}}{{{\rm{AC}}}}{\rm{khi\;}} \Rightarrow {\rm{ABC\;vu\^o ng}}\)
Theo hệ thức lượng trong tam giác vuông và định lí Pytago ta có
\({\rm{B}}{{\rm{C}}^2} = {\rm{BH}}.{\rm{BA}} = {\rm{A}}{{\rm{B}}^2} - {\rm{A}}{{\rm{C}}^2} \Leftrightarrow {\rm{A}}{{\rm{B}}^2} - {\rm{BH}}.{\rm{BA}} - {\rm{A}}{{\rm{C}}^2} = 0\left( 4 \right)\)
Từ (3) và(4) ta có 2\({\rm{A}}{{\rm{B}}^2} - {\rm{AB}}.{\rm{AC}} - 2{\rm{A}}{{\rm{C}}^2} = 0\)(5)
Vì AC>0, chia 2 vế cho \(A{C^2}\) ta được phương trình bậc 2 với \(x = \frac{{AB}}{{AC}}\) là: \(2{x^2} - {\rm{x}} - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{x}} = \frac{{1 + \sqrt {17} }}{4}}\\{{\rm{x}} = \frac{{1 - \sqrt {17} }}{4}}\end{array}} \right.\)
Do \(\frac{{1 - \sqrt {17} }}{4} < 0{\rm{\;}}\left( {{\rm{loai}}} \right)\) nên ta chọn \({\rm{x}} = \frac{{1 + \sqrt {17} }}{4}\), hay \(\frac{{{\rm{AB}}}}{{{\rm{AC}}}} = \frac{{1 + \sqrt {17} }}{4}\)
Lời giải
Ta có biểu thức:\(\Delta = {{\rm{b}}^2} - 4{\rm{ac}} = {{\rm{b}}^2} - 4{\rm{a}}\left( {{\rm{b}} - 2{\rm{a}}} \right) = {\left( {2{\rm{a}} - {\rm{b}}} \right)^2} + 4{{\rm{a}}^2} > 0,\forall {\rm{a}} \ne 0\); do đó, phương trình luôn có 2 nghiệm phân biệt.
Giả sử 2 nghiệm đã cho là \({{\rm{x}}_1},{{\rm{x}}_2}\).Theo định lí Viét, ta có \(\left\{ {\begin{array}{*{20}{c}}{{{\rm{x}}_1} + {{\rm{x}}_2} = - \frac{{\rm{b}}}{{\rm{a}}}}\\{{{\rm{x}}_1}{{\rm{x}}_2} = \frac{{\rm{c}}}{{\rm{a}}}}\end{array}} \right.\)
Từ giả thiết \(2{\rm{a}} - {\rm{b}} + {\rm{c}} = 0 \Rightarrow \frac{{\rm{b}}}{{\rm{a}}} - \frac{{\rm{c}}}{{\rm{a}}} = 2\), do đó
\( - \left( {{{\rm{x}}_1} + {{\rm{x}}_2}} \right) - {{\rm{x}}_1}{{\rm{x}}_2} = 2\left( {{{\rm{x}}_1} + 1} \right)\left( {{{\rm{x}}_2} + 1} \right) = - 1\)(*). Nếu 2 nghiệm đều dương thì \(\left( {{{\rm{x}}_1} + 1} \right)\left( {{{\rm{x}}_2} + 1} \right) > 1\), mâu thuẫn với (*).
Vậy 2 nghiệm của phương trình không thể đều dương.
Lời giải
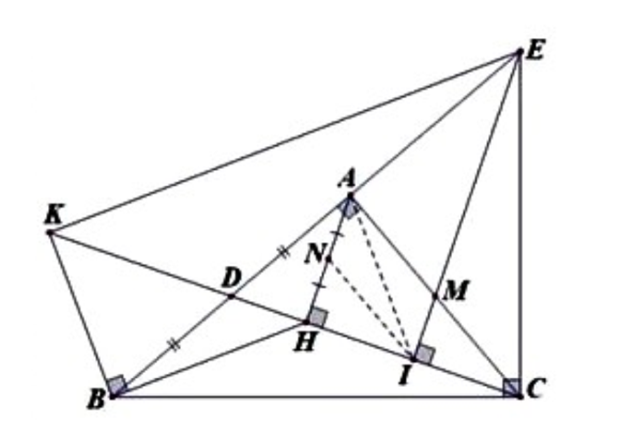
a) Chứng minh \({\rm{BH}} \bot {\rm{AI}}\)
Gọi \({\rm{M}}\) là giao điểm của \({\rm{EI}}\) và \({\rm{AC}}\), ta có \({\rm{M}}\) là trực tâm của tam giác \({\rm{ECD}} \Rightarrow {\rm{DM}}\)//\({\rm{BC}}\)..
Tam giác ABC có
\({\rm{DA}} = {\rm{DB}},{\rm{\;DM}}\parallel {\rm{BC}} \Rightarrow {\rm{MA}} = {\rm{MC}}\).
Tam giác \({\rm{AHC}}\) có
\({\rm{MA}} = {\rm{MC}},{\rm{\;MI}}\parallel {\rm{AH}} \Rightarrow {\rm{IH}} = {\rm{IC}}\).
Gọi \({\rm{N}}\) là trung điểm của \({\rm{AH}}\) ta có \({\rm{IN}}\parallel {\rm{AC}} \Rightarrow {\rm{IN}} \bot {\rm{AD}}\).
Tam giác \({\rm{ADI\;c\'o }}\)
\({\rm{AH}} \bot {\rm{DI}},{\rm{\;IN}} \bot {\rm{AD}}\) do đó \({\rm{N}}\) là trực tâm \( \Rightarrow {\rm{DN}} \bot {\rm{AI}} \Rightarrow {\rm{BH}} \bot {\rm{AI}}\).
b) Chứng minh tứ giác \({\rm{BCEK}}\) nội tiếp
Từ \({\rm{BH}} \bot {\rm{AI\;}} \Rightarrow {\rm{IN}}\parallel {\rm{AC}} \Rightarrow \widehat {{\rm{IAD}}} = \widehat {{\rm{KBD}}}\)
Xét \(\Delta {\rm{KBD\;v\`a \;}}\Delta {\rm{IAD}}\) có:
\(\widehat {{\rm{IAD}}} = \widehat {{\rm{KBD}}},{\rm{\;DA}} = {\rm{DB}},{\rm{\;}}\widehat {{\rm{ADI}}} = \widehat {{\rm{BDK}}} \Rightarrow \Delta {\rm{KBD\;}} = {\rm{\;}}\Delta {\rm{IAD}}\)
\( \Rightarrow {\rm{DK}} = {\rm{DI}}\) (1).
Vì \(\Delta {\rm{DAC\;}}\~{\rm{\;}}\Delta {\rm{DIE}}\) (g.g) \( \Rightarrow \frac{{{\rm{DA}}}}{{{\rm{DI}}}} = \frac{{{\rm{DC}}}}{{{\rm{DE}}}} \Rightarrow {\rm{DA}}.{\rm{DE}} = {\rm{DI}}.{\rm{DC}}\)(2).
Từ (1) và (2) kết hợp với \({\rm{DA}} = {\rm{DB}}\) suy ra \({\rm{DA}}.{\rm{DE}} = {\rm{DK}}.{\rm{DC}}\)
\( \Rightarrow \frac{{{\rm{DK}}}}{{{\rm{DE}}}} = \frac{{{\rm{DB}}}}{{{\rm{DC}}}} \Rightarrow \Delta {\rm{DEK\;}}\~{\rm{\;}}\Delta {\rm{DCB}} \Rightarrow \widehat {{\rm{DEK}}} = \widehat {{\rm{DCB}}}\)dẫn đến \({\rm{BCEK}}\) nội tiếp.