Đề thi tuyển sinh vào lớp 10 Toán năm học 2015 - 2016 Sở GD&ĐT Đà Nẵng có đáp án

xxxx\[A = \left( {\frac{{\sqrt {21}  - \sqrt 7 }}{{\sqrt 3  - 1}} + \frac{{\sqrt {10}  - \sqrt 5 }}{{\sqrt 2  - 1}}} \right):\frac{1}{{\sqrt 7  - \sqrt 5 }}\]

xxx\[ = \left[ {\frac{{\sqrt 7 \left( {\sqrt 3  - 1} \right)}}{{\sqrt 3  - 1}} + \frac{{\sqrt 5 \left( {\sqrt 2  - 1} \right)}}{{\sqrt 2  - 1}}} \right]\left( {\sqrt 7  - \sqrt 5 } \right)\]

xxx\[ = \left( {\sqrt 7  + \sqrt 5 } \right)\left( {\sqrt 7  - \sqrt 5 } \right) = 7 - 5 = 2\]

Vậy xxx\[A = 2\].

Điều kiện: xxxx\[x \ne 0\].

Đặt xxx\[\frac{1}{x} = u\] xxxxx\[\left( {u \ne 0} \right)\], khi đó hệ phương trình đã cho trở thành

xxxx\[\left\{ \begin{array}{l}\frac{3}{2}u - y = 6\\u + 2y =  - 4\end{array} \right.\]xxxxxxxxx\[ \Leftrightarrow \left\{ \begin{array}{l}3u - 2y = 12\,\,\,\,\,\,\,\,\left( 1 \right)\\3u + 6y =  - 12\,\,\,\,\,\left( 2 \right)\end{array} \right.\]

Lấy (2) trừ vế theo vế cho (1) ta được: xxx\[8y =  - 24 \Leftrightarrow y =  - 3\].

Thay xxxxxx\[y =  - 3\] vào (1) suy ra xxxx\[u = 2\] (t/m), do đó xxxx\[\frac{1}{x} = 2 \Rightarrow x = \frac{1}{2}\] (t/m).

Vậy hệ có nghiệm duy nhất xxxxxx\[\left\{ \begin{array}{l}x = \frac{1}{2}\\y =- 3\end{array} \right.\].

1) Lập bảng giá trị và vẽ đồ thị hàm số xxxx\[y = {x^2}\].

Đồ thị xxxxxxx\[\left( P \right)\] là đường cong đi qua các điểm xxx\[\left( { - 2;\,4} \right),\,\left( { - 1;\,1} \right),\,\left( {0;\,0} \right),\,\left( {1;\,1} \right),\,\left( {2;\,4} \right)\].

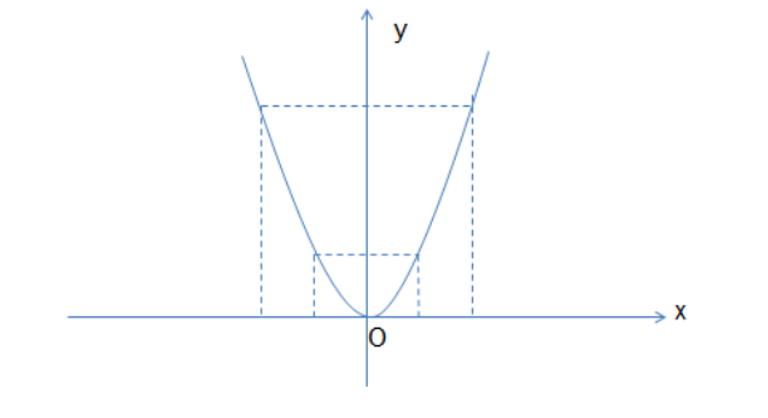
2) Phương trình hoành độ giao điểm của xxxxxx\[\left( P \right)\] và xxxxxxx\[\left( d \right)\] là: xxxxx\[{x^2} = x + 2\]

xxxxx\[ \Leftrightarrow {x^2} - x - 2 = 0\] (*)

Phương trình (*) có dạng xxxxxx\[a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\] nên có 2 nghiệm: xxxxxx\[\left\{ \begin{array}{l}{x_1} =  - 1\\{x_2} = \frac{{ - c}}{a} = 2\end{array} \right.\].

Do đó, xxx\[\left( d \right)\] cắt xxxx\[\left( P \right)\] tại hai điểm xxxxxxx\[A\left( { - 1;\,1} \right)\] và xxxxxx\[B\left( {2;\,4} \right)\].

Để xxxxxxxxx\[\left( P \right)\], xxxxxxx\[\left( d \right)\] và xx\[\left( {{d_m}} \right)\] cùng đi qua một điểm thì hoặc xxxx\[A \in \left( {{d_m}} \right)\] hoặc xxxx\[B \in \left( {{d_m}} \right)\].

+ Với xxxxxxx\[A\left( { - 1;\,1} \right) \in \left( {{d_m}} \right)\], ta có: xxx\[1 =  - \left( { - 1} \right) + m \Leftrightarrow m = 0\].

+ Với xxxx\[B\left( {2;\,4} \right) \in \left( {{d_m}} \right)\], ta có: xxx\[4 =  - 2 + m \Leftrightarrow m = 6\].

Vậy khi xxxx\[m = 0\] hoặc xxxx\[m = 6\]  thì xxxxxx\[\left( P \right)\] , xxx\[\left( d \right)\] và xxxxxxx\[\left( {{d_m}} \right)\] cùng đi qua một điểm.

1) Thay xxx\[m = 1\] vào phương trình đã cho ta được: xxxxx\[{x^2} - 2 = 0 \Leftrightarrow {x^2} = 2 \Leftrightarrow x =  \pm \sqrt 2 \].

Vậy khi xxx\[m = 1\], phương trình đã cho có hai nghiệm xxxx\[x = \sqrt 2 \] và xxx\[x =  - \sqrt 2 \].

2) Có xxxxxxx\[\Delta  = 4{\left( {m - 1} \right)^2} - 4.\left( { - 2m} \right) = 4{m^2} - 8m + 4 + 8m = 4{m^2} + 4 > 0\] với mọi xxx\[m\] nên phương trình đã cho luôn có 2 nghiệm phân biệt với mọi xx\[m\].

Vì xxx\[{x_1}\] và xxxx\[{x_2}\] là hai nghiệm của phương trình đã cho nên theo định lí Vi-et ta có:

 xxxx\[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 2m - 2\,\,\,\,\,\,\left( 1 \right)\\{x_1}.{x_2} = \frac{c}{a} =  - 2m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]

Theo bài ta có xxxx\[x_1^2 + {x_1} - {x_2} = 5 - 2m\] (3).

Từ (1) và (3) ta có hệ (I): xxxxxxxx\[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 2\\{x_1}^2 + {x_1} - {x_2} = 5 - 2m\end{array} \right.\]

xxxxx\[ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2m - 2 - {x_1}\\{x_1}^2 + {x_1} - \left( {2m - 2 - {x_1}} \right) = 5 - 2m\end{array} \right.\]

xxx\[ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2m - 2 - {x_1}\\{x_1}^2 + 2{x_1} = 3\end{array} \right.\]

Từ hệ (I) có PT : xxx\[x_1^2 + 2{x_1} - 3 = 0\]. Từ đó suy ra xxx\[\left[ \begin{array}{l}{x_1} = 1\\{x_1} =  - 3\end{array} \right.\]

+ Với xxxx\[{x_1} = 1\] thì xxx\[{x_2} = 2m - 2 - {x_1} = 2m - 2 - 1 = 2m - 3\].

Thay vào (2) ta được: xxxxxxxx\[1.\left( {2m - 3} \right) =  - 2m \Leftrightarrow 4m = 3 \Leftrightarrow m = \frac{3}{4}\].

+ Với xxxxxx\[{x_1} =  - 3\], tương tự như trên ta có xxx\[m =  - \frac{3}{4}\].

Vậy khi xxx\[m =  \pm \frac{3}{4}\] thì thỏa mãn yêu cầu bài toán.