Cho phương trình \[{x^2} - 2\left( {m - 1} \right)x - 2m = 0\], với \[m\] là tham số.
1) Giải phương trình khi \[m = 1\].
2) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi \[m\]. Gọi \[{x_1}\] và \[{x_2}\] là hai nghiệm của phương trình, tìm tất cả các giá trị của \[m\] sao cho \[x_1^2 + {x_1} - {x_2} = 5 - 2m\].
Cho phương trình \[{x^2} - 2\left( {m - 1} \right)x - 2m = 0\], với \[m\] là tham số.
1) Giải phương trình khi \[m = 1\].
2) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi \[m\]. Gọi \[{x_1}\] và \[{x_2}\] là hai nghiệm của phương trình, tìm tất cả các giá trị của \[m\] sao cho \[x_1^2 + {x_1} - {x_2} = 5 - 2m\].
Quảng cáo
Trả lời:
1) Thay xxx\[m = 1\] vào phương trình đã cho ta được: xxxxx\[{x^2} - 2 = 0 \Leftrightarrow {x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \].
Vậy khi xxx\[m = 1\], phương trình đã cho có hai nghiệm xxxx\[x = \sqrt 2 \] và xxx\[x = - \sqrt 2 \].
2) Có xxxxxxx\[\Delta = 4{\left( {m - 1} \right)^2} - 4.\left( { - 2m} \right) = 4{m^2} - 8m + 4 + 8m = 4{m^2} + 4 > 0\] với mọi xxx\[m\] nên phương trình đã cho luôn có 2 nghiệm phân biệt với mọi xx\[m\].
Vì xxx\[{x_1}\] và xxxx\[{x_2}\] là hai nghiệm của phương trình đã cho nên theo định lí Vi-et ta có:
xxxx\[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 2m - 2\,\,\,\,\,\,\left( 1 \right)\\{x_1}.{x_2} = \frac{c}{a} = - 2m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Theo bài ta có xxxx\[x_1^2 + {x_1} - {x_2} = 5 - 2m\] (3).
Từ (1) và (3) ta có hệ (I): xxxxxxxx\[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 2\\{x_1}^2 + {x_1} - {x_2} = 5 - 2m\end{array} \right.\]
xxxxx\[ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2m - 2 - {x_1}\\{x_1}^2 + {x_1} - \left( {2m - 2 - {x_1}} \right) = 5 - 2m\end{array} \right.\]
xxx\[ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2m - 2 - {x_1}\\{x_1}^2 + 2{x_1} = 3\end{array} \right.\]
Từ hệ (I) có PT : xxx\[x_1^2 + 2{x_1} - 3 = 0\]. Từ đó suy ra xxx\[\left[ \begin{array}{l}{x_1} = 1\\{x_1} = - 3\end{array} \right.\]
+ Với xxxx\[{x_1} = 1\] thì xxx\[{x_2} = 2m - 2 - {x_1} = 2m - 2 - 1 = 2m - 3\].
Thay vào (2) ta được: xxxxxxxx\[1.\left( {2m - 3} \right) = - 2m \Leftrightarrow 4m = 3 \Leftrightarrow m = \frac{3}{4}\].
+ Với xxxxxx\[{x_1} = - 3\], tương tự như trên ta có xxx\[m = - \frac{3}{4}\].
Vậy khi xxx\[m = \pm \frac{3}{4}\] thì thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Từ một điểm A nằm bên ngoài đường tròn ( O), kẻ các tiếp tuyến AB,AC với đường tròn (\[B,\,C\] là các tiếp điểm). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/blobid1-1761841295.png)
1) Ta có xxxxxx\[AB \bot OB\] (t/c tiếp tuyến) xxx\[ \Rightarrow \widehat {ABO} = 90^\circ \].
xxx\[AC \bot OC\](t/c tiếp tuyến) xxx\[ \Rightarrow \widehat {ACO} = 90^\circ \]
Xét tứ giác xxx\[ABOC\] có xxx\[\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ \] nên nội tiếp được trong đường tròn.
2) Vì xxxx\[AB\] và xxxx\[AC\] là hai tiếp tuyến của đường tròn xxx\[\left( O \right)\] nên xxxxxx\[AO\] là đường trung trực của xxxxxx\[BC\]. Gọi xxxx\[H\] là giao điểm của xxx\[AO\] và xxxx\[BC\], khi đó xx\[H\] là trung điểm của xxx\[BC\] nên ta cóxxxxxxx\[BC = 2BH\].
Lại có xxxxx\[\Delta ABO\] vuông tại xxxxxx\[B\] có xxx\[BH\] là đường cao nên xxxx\[O{B^2} = OH.OA\]
xxxxx\[ \Rightarrow OH = \frac{{O{B^2}}}{{OA}} = \frac{{{3^2}}}{5} = \frac{9}{5}\,\,\left( {{\rm{cm}}} \right)\].
Tam giác xxx\[OBH\] vuông tại xxxxxx\[H\] nên từ định lí Pytago ta suy ra
xxxx\[BH = \sqrt {O{B^2} - O{H^2}} = \sqrt {{3^2} - {{\left( {\frac{9}{5}} \right)}^2}} = \frac{{12}}{5}\,\,\left( {{\rm{cm}}} \right)\]
Vậy xxxx\[BC = 2BH = 2.\frac{{12}}{5} = \frac{{24}}{5}\,\,\left( {{\rm{cm}}} \right)\].
3) Gọi xxxxx\[E\] là giao điểm của xxx\[BM\] và xxxx\[AC\].
Xét xxx\[\Delta EMC\] và xxx\[\Delta ECB\] có:
xxxx\[\widehat {MEC} = \widehat {CEB}\] (Góc chung)
xxx\[\widehat {MCE} = \widehat {EBC}\] (Góc nội tiếp và góc tạo bởi tia tiếp tuyến xxxx\[CA\] cùng chắn cung xxxx\[MC\] của đường tròn xxxx\[\left( O \right)\])
Do đó, xx (g – g).
x\[ \Rightarrow \frac{{EM}}{{EC}} = \frac{{EC}}{{EB}} \Rightarrow E{C^2} = EM.EB\] (*)
Ta có xxxx\[\widehat {MAE} = \widehat {MCB}\] (Góc nội tiếp và góc tạo bởi tia tiếp tuyến xxxxxx\[CB\] cùng chắn cung xx\[MC\] của đường tròn xxx\[\left( K \right)\]).
Và xx\[\widehat {MCB} = \widehat {ABE}\] (Góc nội tiếp và góc tạo bởi tia tiếp tuyến xxxxxxx\[BA\] cùng chắn cung xxxxxx\[MB\] của đường tròn xxx\[\left( O \right)\]).
Do đó, xxx\[\widehat {MAE} = \widehat {ABE}\].
Xét xxx\[\Delta EMA\] và xxxx\[\Delta EAB\] có:
xxxx\[\widehat {MEA} = \widehat {AEB}\] (góc chung)
xxx\[\widehat {MAE} = \widehat {ABE}\] (cmt)
Do đó, xxx (g – g).
xxx\[ \Rightarrow \frac{{EM}}{{EA}} = \frac{{EA}}{{EB}} \Rightarrow E{A^2} = EM.EB\] (**)
Từ (*) và (**) xxxx\[ \Rightarrow E{C^2} = E{A^2} \Rightarrow EC = EA\].
Vậy đường thẳng xxxxx\[BM\] đi qua trung điểm xxx\[E\] của đoạn thẳng xxx\[AC\].
Lời giải
1) Lập bảng giá trị và vẽ đồ thị hàm số xxxx\[y = {x^2}\].
|
xxx\[x\] |
– 2 |
– 1 |
0 |
1 |
2 |
|
xxx\[y\] |
4 |
1 |
0 |
1 |
4 |
Đồ thị xxxxxxx\[\left( P \right)\] là đường cong đi qua các điểm xxx\[\left( { - 2;\,4} \right),\,\left( { - 1;\,1} \right),\,\left( {0;\,0} \right),\,\left( {1;\,1} \right),\,\left( {2;\,4} \right)\].
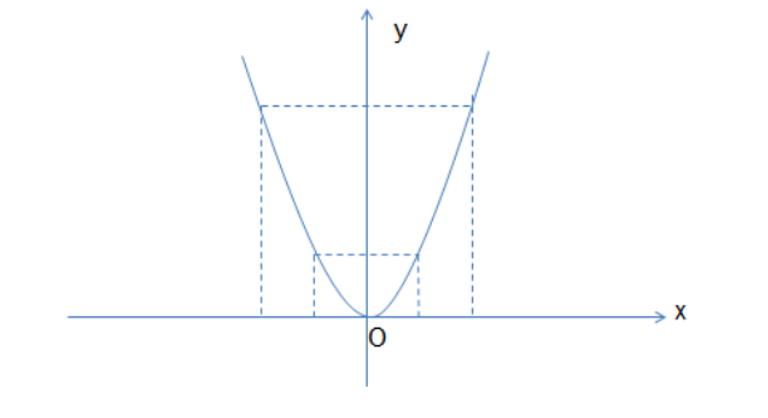
2) Phương trình hoành độ giao điểm của xxxxxx\[\left( P \right)\] và xxxxxxx\[\left( d \right)\] là: xxxxx\[{x^2} = x + 2\]
xxxxx\[ \Leftrightarrow {x^2} - x - 2 = 0\] (*)
Phương trình (*) có dạng xxxxxx\[a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\] nên có 2 nghiệm: xxxxxx\[\left\{ \begin{array}{l}{x_1} = - 1\\{x_2} = \frac{{ - c}}{a} = 2\end{array} \right.\].
Do đó, xxx\[\left( d \right)\] cắt xxxx\[\left( P \right)\] tại hai điểm xxxxxxx\[A\left( { - 1;\,1} \right)\] và xxxxxx\[B\left( {2;\,4} \right)\].
Để xxxxxxxxx\[\left( P \right)\], xxxxxxx\[\left( d \right)\] và xx\[\left( {{d_m}} \right)\] cùng đi qua một điểm thì hoặc xxxx\[A \in \left( {{d_m}} \right)\] hoặc xxxx\[B \in \left( {{d_m}} \right)\].
+ Với xxxxxxx\[A\left( { - 1;\,1} \right) \in \left( {{d_m}} \right)\], ta có: xxx\[1 = - \left( { - 1} \right) + m \Leftrightarrow m = 0\].
+ Với xxxx\[B\left( {2;\,4} \right) \in \left( {{d_m}} \right)\], ta có: xxx\[4 = - 2 + m \Leftrightarrow m = 6\].
Vậy khi xxxx\[m = 0\] hoặc xxxx\[m = 6\] thì xxxxxx\[\left( P \right)\] , xxx\[\left( d \right)\] và xxxxxxx\[\left( {{d_m}} \right)\] cùng đi qua một điểm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.