Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 1
166 người thi tuần này 4.6 471 lượt thi 11 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Đoạn văn 1
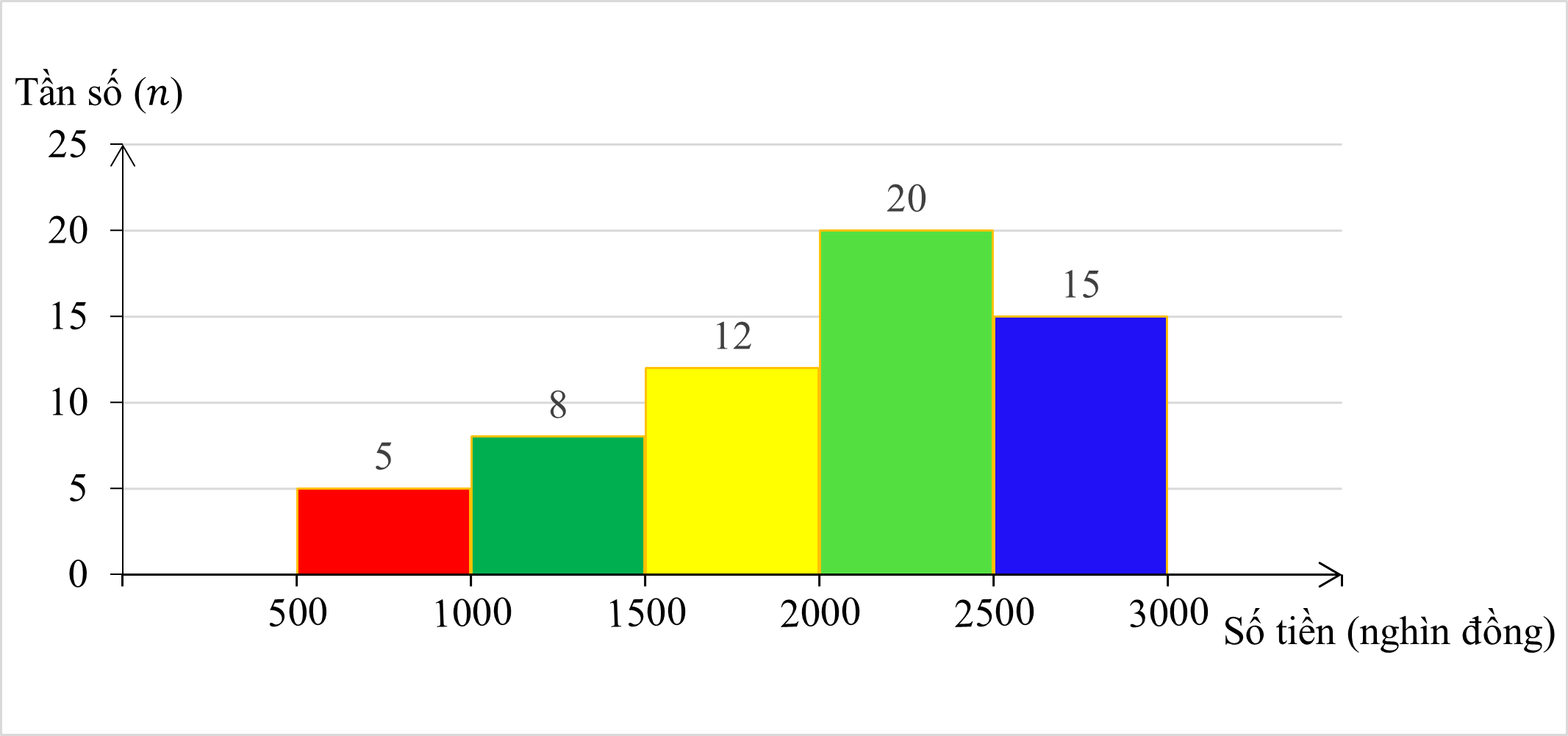
(1,5 điểm) Một cửa hàng tạp hóa thống kê số tiền lãi (đơn vị: nghìn đồng) trong \(60\) ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm sau:
Lời giải
Tần số tương đối của mỗi nhóm là:
\[{f_1} = \frac{{5.100}}{{60}}\% = 8,3\% \];\[{f_2} = \frac{{8.100}}{{60}}\% = 13,4\% \];\[{f_3} = \frac{{12.100}}{{60}}\% = 20\% \];\[{f_4} = \frac{{20.100}}{{60}}\% = 33,3\% \];\[{f_5} = \frac{{15.100}}{{60}}\% = 25\% \]
Lời giải
Bảng tần số tương đối ghép nhóm của mẫu số liệu đã cho là:
|
Số tiền (nghìn đồng) |
\(\left[ {500\,;\,\,1000} \right)\) |
\(\left[ {1000\,;\,\,1500} \right)\) |
\(\left[ {1500\,\,;\,\,2000} \right)\) |
\(\left[ {2000\,\,;\,\,2500} \right)\) |
\(\left[ {2500\,\,;\,\,3000} \right)\) |
|
Tần số tương đối |
\(8,3\% \) |
\(13,4\% \) |
\(20\% \) |
\(33,3\% \) |
\(25\% \) |
Đoạn văn 2
(1,5 điểm) Cho hai biểu thức: A = và B = - với x > 0, x > 4
Lời giải
Có \[A = \frac{{x - 3}}{{\sqrt x }}\] \[\left( {x > 0,x \ne 4} \right)\]
Thay \[x = 16\] (TMĐK) vào biểu thức \[A\] ta có:
\[A = \frac{{16 - 3}}{{\sqrt {16} }} = \frac{{13}}{4}\]
Vậy \[A = \frac{{13}}{4}\] khi \[x = 16\]
Lời giải
Rút gọn \[B\]:
\[B = \frac{{\sqrt x }}{{\sqrt x + 2}} - \frac{{4\sqrt x }}{{4 - x}}(x > 0,x \ne 4)\]
\[B = \frac{{\sqrt x }}{{\sqrt x + 2}} + \frac{{4\sqrt x }}{{(\sqrt x - 2)(\sqrt {x + 2} )}}\]
\[B = \frac{{\sqrt x (\sqrt x - 2)}}{{(\sqrt x - 2)(\sqrt {x + 2} )}} + \frac{{4\sqrt x }}{{(\sqrt x - 2)(\sqrt {x + 2} )}}\]
\[B = \frac{{x - 2\sqrt x + 4\sqrt x }}{{(\sqrt x - 2)(\sqrt {x + 2} )}}\]
\[B = \frac{{x + 2\sqrt x }}{{(\sqrt x - 2)(\sqrt {x + 2} )}}\]
\[B = \frac{{\sqrt x (\sqrt x + 2)}}{{(\sqrt x - 2)(\sqrt {x + 2} )}}\]
\[B = \frac{{\sqrt x }}{{\sqrt x - 2}}\]
Vậy \[B = \frac{{\sqrt x }}{{\sqrt x - 2}}\] với \[x > 0,x \ne 4\]
Lời giải
Có \[A = \frac{{x - 3}}{{\sqrt x }}\] và \[B = \frac{{\sqrt x }}{{\sqrt x - 2}}(x > 0,x \ne 4)\]
\[P = A.B\]
\[P = \frac{{x - 3}}{{\sqrt x }} \cdot \frac{{\sqrt x }}{{\sqrt x - 2}}\]
\[P = \frac{{x - 3}}{{\sqrt x - 2}}\]
Để \[P \le 6\] thì \[\frac{{x - 3}}{{\sqrt x - 2}} \le 6\]
\[\frac{{x - 3}}{{\sqrt x - 2}} - 6 \le 0\]
\[\frac{{x - 3 - 6(\sqrt x - 2)}}{{\sqrt x - 2}} \le 0\]
\[\frac{{x - 3 - 6\sqrt x + 12}}{{\sqrt x - 2}} \le 0\]
\[\frac{{x - 6\sqrt x + 9}}{{\sqrt x - 2}} \le 0\]
\[\frac{{{{\left( {\sqrt x - 3} \right)}^2}}}{{\sqrt x - 2}} \le 0\]
TH1: \[\frac{{{{\left( {\sqrt x - 3} \right)}^2}}}{{\sqrt x - 2}} = 0\]
\[{\left( {\sqrt x - 3} \right)^2} = 0\]
\[\sqrt x - 3 = 0\]
\[\sqrt x = 3\]
\[x = 9\] (TMĐK)
TH2: \[\frac{{{{\left( {\sqrt x - 3} \right)}^2}}}{{\sqrt x - 2}} < 0\]
Mà \[{\left( {\sqrt x - 3} \right)^2} \ge 0,\forall x\] TMĐKXĐ
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {\sqrt x - 3} \right)}^2} > 0}\\{\sqrt x - 2 < 0}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\sqrt x - 3 \ne 0}\\{\sqrt x < 2}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\sqrt x \ne 3}\\{x < 4}\end{array}} \right.\]
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 9}\\{x < 4}\end{array}} \right.\]
\[ \Rightarrow x < 4\] mà \[x > 0,x \ne 4\] và \[x\] là số nguyên \[ \Rightarrow x \in \{ 1;2;3\} \]
Vậy để \[P \le 6\] thì \[x \in \{ 1;2;3;9\} \]
Đoạn văn 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.