Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Bình Phước có đáp án
41 người thi tuần này 4.6 65 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1)Tính giá trị của các biểu thức sau:
\[A = \sqrt {16} + \sqrt 9 \] \[B = \sqrt 7 + \sqrt {{{\left( {4 - \sqrt 7 } \right)}^2}} .\]
\[A = 4 + 3 = 7\]
\[B = \sqrt 7 + 4 - \sqrt 7 = 4\]
2)Cho biểu thức \[P = \frac{{x - 9}}{{\sqrt x + 3}} + \sqrt x + 2\] với \[x \ge 0\].a) Rút gọn biểu thức \[P.\]
b) Tính giá trị của biểu thức \[P\] khi \[x = 4\].
\[P = \frac{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}{{\sqrt x + 3}} + \sqrt x + 2 = \sqrt x - 3 + \sqrt x + 2 = 2\sqrt x - 1\]
\[x = 4 \Rightarrow P = 2.\sqrt 4 - 1 = 3\]
Lời giải
|
1) aVẽ Parabol \[(P)\] và đường thẳng \[(d)\]trên cùng một hệ trục toạ độ \[Oxy.\] |
||||||||||||||||||
|
Bảng giá trị
|
||||||||||||||||||
|
Đồ thị 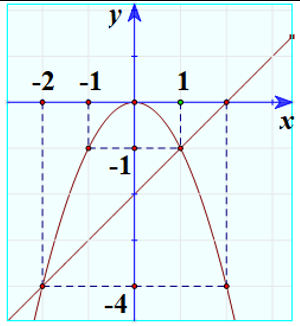 |
||||||||||||||||||
|
b)Tìm toạ độ giao điểm của Parabol \[(P)\] và đường thẳng \[(d)\] bằng phép tính. |
||||||||||||||||||
|
Phương trình hoành độ giao điểm của Parabol \[(P)\] và đường thẳng \[(d)\] là \[ - {x^2} = x - 2 \Leftrightarrow - {x^2} - x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = - 4\\x = 1 \Rightarrow y = - 1\end{array} \right.\]. Vậy \[(P)\] cắt \[(d)\] tại hai điểm có toạ độ lần lượt là \[( - 2; - 4)\] và \[(1; - 1).\] |
||||||||||||||||||
|
2.Không sử dụng máy tính, giải hệ phương trình: \[\left\{ \begin{array}{l}2x + y = 5\\x - 3y = - 1\end{array} \right.\]. |
||||||||||||||||||
|
Ta có \[\left\{ \begin{array}{l}2x + y = 5\\x - 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x + 3y = 15\\x - 3y = - 1\end{array} \right..\] |
||||||||||||||||||
|
\[ \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\x - 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - 3y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\] |
||||||||||||||||||
|
Vậy phương trình có nghiệm duy nhất \[\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\]. |
Lời giải
.1a)Giải phương trình khi \[m = 0.\]
.Khi \[m = 0\] ta có phương trình \[{x^2} - 2x - 3 = 0\]
\[\Delta = {\left( { - 2} \right)^2} + 12 = 16 \Rightarrow \sqrt \Delta = 4.\]
.Phương trình có hai nghiệm phân biệt
\[{x_1} = \frac{{2 + 4}}{2} = 3,\,\,{x_2} = \frac{{2 - 4}}{2} = - 1\]
.b)Tìm \[m\] để phương trình có hai nghiệm \[{x_1},\,\,{x_2}\] sao cho biểu thức \[P = x_1^2 + x_2^2 + {\left( {{x_1}{x_2}} \right)^2}\] đạt giá trị nhỏ nhất.
.Ta có \[\Delta = {\left( { - 2} \right)^2} - 4\left( {m - 3} \right) = - 4m + 16\]
Để phương trình có hai nghiệm thì
\[\Delta \ge 0 \Leftrightarrow - 4m + 16 \ge 0 \Leftrightarrow m \le 4.\]
.Theo hệ thức Viét ta có \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 3\end{array} \right.\].
Tacó
\[P = x_1^2 + x_2^2 + {\left( {{x_1}{x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2} = {2^2} - 2\left( {m - 3} \right) + {\left( {m - 3} \right)^2}\]
\[P = {m^2} - 8m + 19 = {\left( {m - 4} \right)^2} + 3 \ge 3.\]
.Dấu bằng xảy ra khi \[m = 4.\] Vậy giá trị nhỏ nhất của \[P\] là \[3\] khi \[m = 4.\]
.2.Một mảnh vườn hình chữ nhật có diện tích \[600\,{{\rm{m}}^2}\]. Biết rằng nếu tăng chiều dài \[10\,{\rm{m}}\] và giảm chiều rộng \[5\,{\rm{m}}\] thì diện tích không đổi. Tính chiều dài và chiều rộng của mảnh vườn.
.Gọi chiều rộng khu vườn hình chữ nhật là \[x\,\,\left( {\rm{m}} \right),\] \[x > 5.\]
Suy ra chiều dài khu vườn là \[\frac{{600}}{x}\,\,\left( {\rm{m}} \right).\]
.Chiều dài khu vườn sau khi tăng là \[\frac{{600}}{x} + 10\,\,\left( {\rm{m}} \right).\]
Chiều rộng khu vườn sau khi giảm là \[x - 5\,\left( {\rm{m}} \right).\]
.Diện tích khu vườn sau khi tăng chiều dài \[10\,{\rm{m}}\] và giảm chiều rộng \[5\,{\rm{m}}\] thì không đổi nên ta có phương trình
\[\left( {\frac{{600}}{x} + 10} \right)\left( {x - 5} \right) = 600.\]
.\[ \Leftrightarrow \left( {600 + 10x} \right)\left( {x - 5} \right) = 600x \Leftrightarrow 10{x^2} - 50x - 3000 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 20\\x = - 15\,\left( {\rm{L}} \right)\end{array} \right..\]
Vậy chiều dài mảnh vườn là \[30\,\,\left( {\rm{m}} \right),\] chiều rộng mảnh vườn là \[20\,\,\left( {\rm{m}} \right).\]
Lời giải
a.Tính \[\widehat B,\,\,AC,\,\,AH.\]
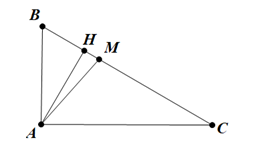
.Ta có \[\widehat B = {60^^\circ }\]
.Ta có \[\sin \widehat C = \frac{{AB}}{{BC}} \Rightarrow BC = \frac{{AB}}{{\sin \widehat C}} = \frac{3}{{\frac{1}{2}}} = 6\,\,\left( {{\rm{cm}}} \right).\]
Ta có \[AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{6^2} - {3^2}} = 3\sqrt 3 \,\,\left( {{\rm{cm}}} \right).\]
.\[AH \cdot BC = AB \cdot AC \Leftrightarrow AH = \frac{{AB \cdot AC}}{{BC}} = \frac{{3 \cdot 3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}\,\left( {{\rm{cm}}} \right).\]
b.Trên cạnh \[BC\]lấy điểm \[M\] sao cho \[MC = 2MB\], tính diện tích tam giác \[AMC.\]
.\[{S_{AMC}} = \frac{1}{2}AH \cdot MC = \frac{1}{2}AH \cdot \frac{2}{3}BC = \frac{1}{2} \cdot \frac{{3\sqrt 3 }}{2} \cdot \frac{2}{3} \cdot 6 = 3\sqrt 3 \,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\]
Lời giải
a.Chứng minh tứ giác \[BODK\] nội tiếp.
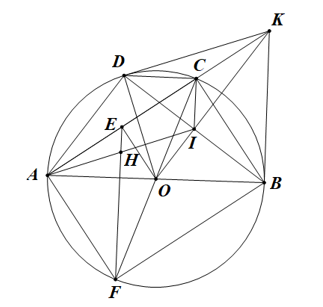
.Ta có \[\widehat {OBK} = \widehat {ODK} = {90^ \circ }.\]
.\[ \Rightarrow \widehat {OBK} + \widehat {ODK} = {180^ \circ }.\]
.Do đó tứ giác \[BODK\] nội tiếp.
b.Gọi \[I\] là giao điểm của \[OK\]và \[BD\]. Chứng minh rằng \[OI \bot BD\] và \[KC \cdot KA = KI \cdot KO.\]
.Ta có \[KB = KD\] (tính chất hai tiếp tuyến cắt nhau)
.Ta lại có \[OB = OD\] nên \[OK\] là đường trung trực của \[BD\]. Suy ra\[KO \bot BD \Rightarrow OI \bot BD.\]
.Xét tam giác \[ABK\] vuông tại \[B\] nên \[K{B^2} = KC.KA.\]
.Xét tam giác \[OBK\] vuông tại \[B\] nên \[K{B^2} = KI \cdot KO.\]
Suy ra \[KC.KA = KI.KO.\] (đpcm)
c.Gọi \[E\] là trung điểm của \[AC\], kẻ đường kính \[CF\] của đường tròn \[(O)\], \[FE\] cắt \[AI\] tại \[H\]. Chứng minh rằng \[H\] là trung điểm của \[AI\].
.Xét tam giác \[KCI\] và tam giác \[KOA\] ta có góc \[K\] chung, \[KC \cdot KA = KI \cdot KO \Leftrightarrow \frac{{KC}}{{KI}} = \frac{{KO}}{{KA}}\]. Suy ra tam giác \[KCI\] và tam giác \[KOA\] đồng dạng với nhau. Suy ra \[\widehat {KCI} = \widehat {KOA}\]. (*)
Xét tam giác \[ACF\] và \[BAK\] có \[\widehat {KBA} = \widehat {C{\rm{AF}}} = {90^^\circ }.\] (1)
Mà tam giác \[O{\rm{AC}}\] cân tại \[O\] nên \[\widehat {OAC} = \widehat {OCA}\] (2)
Từ (1) và (2) suy ra \[\Delta ACF\] đồng dạng với \[\Delta BAK\] suy ra \[\frac{{BA}}{{BK}} = \frac{{AC}}{{{\rm{AF}}}} \Leftrightarrow \frac{{2BO}}{{BK}} = \frac{{2AE}}{{{\rm{AF}}}} \Leftrightarrow \frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\].
.Xét tam giác \[AEF\] và \[BOK\] ta có \[\widehat {KBO} = \widehat {E{\rm{AF}}} = {90^^\circ }\] và \[\frac{{BK}}{{{\rm{AF}}}} = \frac{{BO}}{{AE}}\]
Nên \[\Delta AEF\] đồng dạng với \[\Delta BOK\] suy ra
\[\widehat {AEF} = \widehat {BOK} \Rightarrow \widehat {K{\rm{EF}}} = \widehat {KOA}\]( cùng bù với \[\widehat {AEF}\]) (**)
Từ (*) và (**) ta có \[\widehat {KCI} = \widehat {K{\rm{EF}}}\] suy ra \[{\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\].
Xét tam giác \[ACI\] có \[E\] là trung điểm của \[AC\] và \[{\rm{EF}}\,{\rm{//}}\,{\rm{CI}}\] nên \[H\] là trung điểm của \[AI\].