(0,5 điểm) Cho hình chóp tam giác đều S.ABC có các cạnh bên đều bằng \(6\,\,cm\), độ dài cạnh đáy là \(x\) \[\left( {cm} \right)\]. Tìm \(x\) để diện tích xung quanh của hình chóp đều đó là lớn nhất.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 44 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
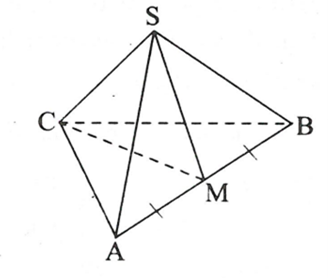
Gọi \[M\] là trung điểm của \[AB\].
Khi đó \[SM\] là trung đoạn của hình chóp.
Ta có \[AB = BC = AC = x\] thì:
\[S{M^2} = S{B^2} - {\left( {\frac{x}{2}} \right)^2} = {6^2} - \frac{{{x^2}}}{4}\]
\[SM = \frac{1}{2}\sqrt {4 \cdot {6^2} - {x^2}} = \frac{1}{2}\sqrt {144 - {x^2}} \]
Diện tích xung quanh của hình chóp là: \[{S_{xq}} = \frac{{3x}}{2}.\frac{1}{2}\sqrt {144 - {x^2}} = \frac{{3x}}{4}\sqrt {144 - {x^2}} \]
Vận dụng bất đẳng thức \[{a^2} + {b^2} \ge 2ab\]hay \[ab \le \frac{{{a^2} + {b^2}}}{2}\]ta được: \[x.\sqrt {144 - {x^2}} \le \frac{{{x^2} + 144 - {x^2}}}{2} = 72\].
Do đó \[{S_{xq}} \le \frac{3}{4}.72 = 54\].
Dấu "=" xảy ra khi\[x = \sqrt {144 - {x^2}} \Leftrightarrow {x^2} = 144 - {x^2} \Leftrightarrow {x^2} = 72 \Leftrightarrow x = 6\sqrt 2 \] .
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Phần ống nhựa cắm vào phân nửa viên kẹo là hình trụ có độ cao \(h = 0,8\,{\rm{cm}}\), bán kính \(r = 0,2\,{\rm{cm}}\)
Thể tích phần ống nhựa cắm vào phân nửa viên kẹo là:
\({V_1} = \pi {r^2}h = \pi \,\,.\,\,{0,2^2}\,\,.\,\,1,6 \approx 0,2\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của viên kẹo tính cả phần ống nhựa cắm vào là:
\({V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \,\,.\,\,{1,6^3} \approx 17,16\,\left( {{\kern 1pt} {\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích thực của viên kẹo sau khi trừ phần ống nhựa:
\(V = {V_{\rm{2}}} - {V_{\rm{1}}} \approx 17,16 - 0,2 = 16,96\,{\kern 1pt} \left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Lời giải
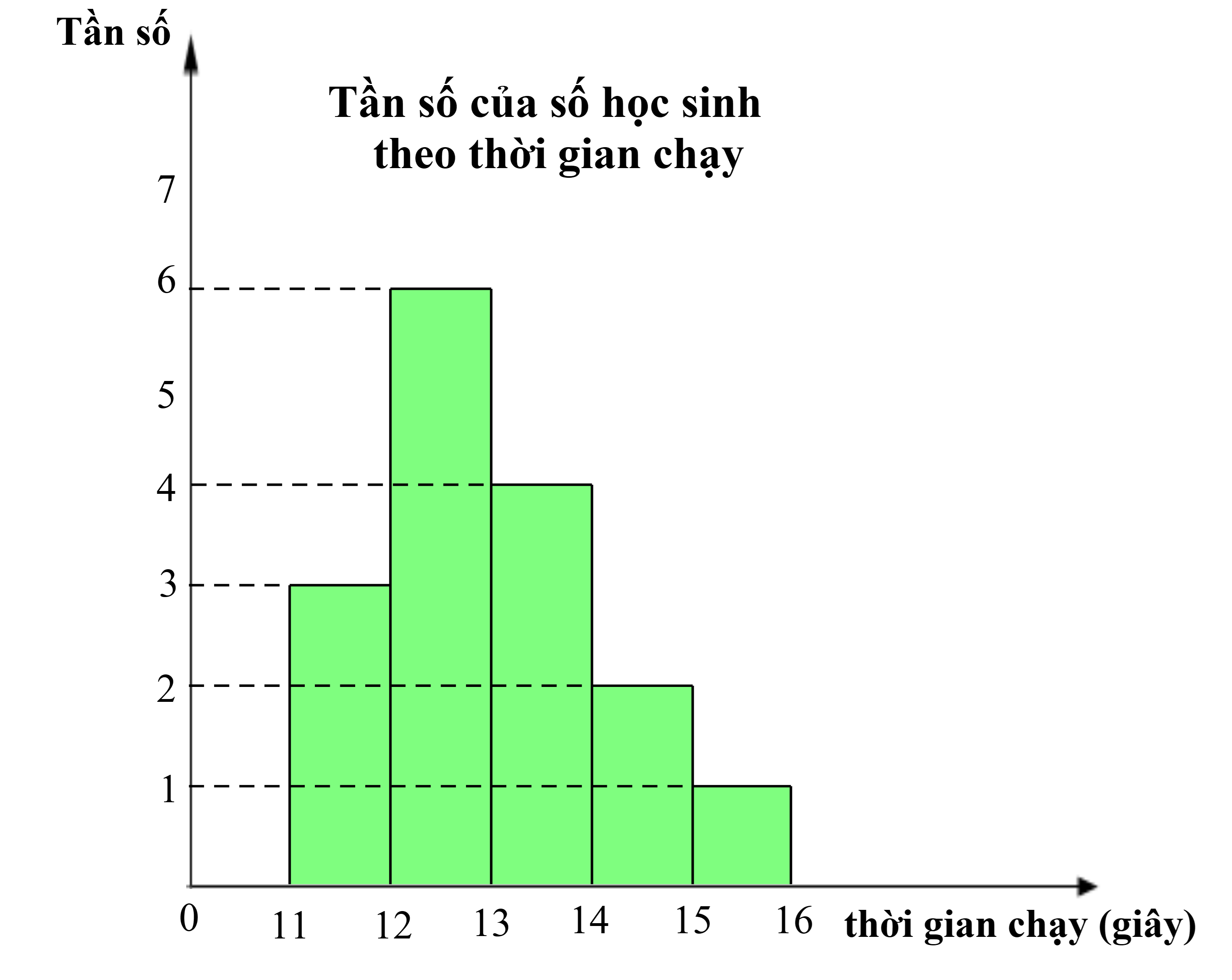
Có \[9\] học sinh chạy \[100\,{\rm{m}}\] hết ít hơn \[13\] giây.
Tần số tương đối ghép nhóm của nhóm \(\left[ {13;14} \right)\) là: \(\frac{4}{{3 + 6 + 4 + 2 + 1}} \cdot 100\% = 25\% \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập