Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
62 người thi tuần này 4.6 1.8 K lượt thi 16 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi khảo sát Toán 9 (chuyên) năm 2026 THPT Chuyên Lê Quý Đôn (TP.HCM) có đáp án
Đề thi thử vào lớp 10 môn Toán (không chuyên) năm 2026 THCS Hậu Giang (TP.HCM) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Nghĩa Mai (Nghệ An) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Lý Sơn (Hà Nội) có đáp án
Đề khảo sát Toán 9 năm 2026 Trường THCS Gia Quất (Hà Nội) Tháng 4/2026 có đáp án
Danh sách câu hỏi:
Câu 1/16
Lời giải
Đáp án đúng là: D
Giải bất phương trình:
\(2x - 10 \ge 0\)
\(2x \ge 10\)
\(x \ge 5.\)
Vậy bất phương trình đã cho có nghiệm là \(x \ge 5\) hay \(5 \le x.\)
Câu 2/16
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Giải phương trình:
\(\left( {2x + 6} \right)\left( {12 - 3x} \right) = 0\)
\(2x + 6 = 0\) hoặc \(12 - 3x = 0\)
\(2x = - 6\) hoặc \(3x = 12\)
\(x = - 3\) hoặc \(x = 4\)
Như vậy, phương trình đã cho có các nghiệm là \(x = - 3;\,\,x = 4.\)
Vậy tập hợp tất cả các nghiệm của phương trình đã cho là \(\left\{ { - 3;\,\,4} \right\}.\)
Câu 3/16
Lời giải
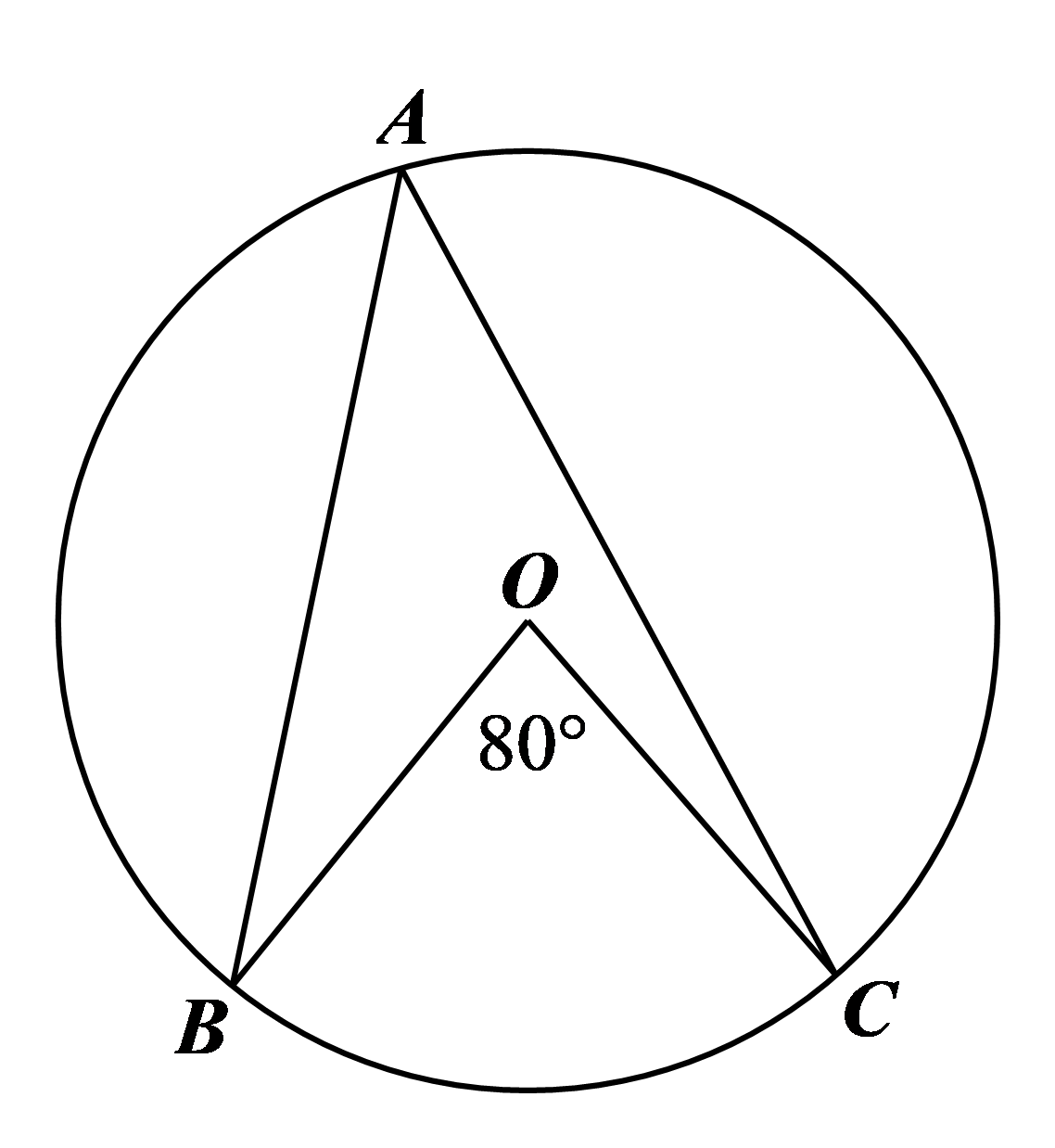
Đáp án đúng là: C
Xét đường tròn \(\left( O \right)\) có \(\widehat {BAC},\,\,\widehat {BOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung \(BC\).
Do đó \[\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2} \cdot 80^\circ = 40^\circ .\]Câu 4/16
Lời giải
Đáp án đúng là: A
Tổng các góc của hình lục giác đều \(ABCDEF\) bằng tổng các góc của hai tứ giác \(ABCD\) và \(ADEF,\) và bằng \(2 \cdot 360^\circ = 720^\circ .\)
Vì \(ABCDEF\) là lục giác đều nên sáu góc của lục giác đều này bằng nhau và bằng: \(\frac{{720^\circ }}{6} = 120^\circ .\)
Vậy \(\widehat {FAB} = 120^\circ .\)Lời giải
Đáp số: \(0,3.\)
Gọi \(A,\,\,B\) lần lượt là hai học sinh nam và \(C,\,\,D,\,\,E\) lần lượt là ba học sinh nữ.
Xét phép thử “chọn ngẫu nhiên 2 học sinh của câu lạc bộ”.
Kết quả của phép thử là cặp chữ \(\left( {X,\,\,Y} \right)\) trong đó \(X,\,\,Y\) lần lượt là tên hai học sinh được chọn.
Không gian mẫu của phép thử trên là:
\[\Omega = \left\{ {\left( {A,\,\,B} \right);\,\,\left( {A,\,\,C} \right);\,\,\left( {A,\,\,D} \right);\,\,\left( {A,\,\,E} \right);\,\,\left( {B,\,\,C} \right);\,\,\left( {B,\,\,D} \right);\,\,\left( {B,\,\,E} \right);\,\,\left( {C,\,\,D} \right);\,\,\left( {C,\,\,E} \right);\,\,\left( {D,\,\,E} \right)} \right\}.\]
Không gian mẫu có 10 phần tử.
Gọi \(M\) là biến cố “2 học sinh được chọn đều là học sinh nữ”.
Có 3 kết quả thuận lợi cho biến cố \(M\), đó là: \(\left( {C,\,\,D} \right),\,\,\left( {C,\,\,E} \right),\,\,\left( {D,\,\,E} \right).\)
Xác suất để cả 2 học sinh được chọn đều là học sinh nữ là: \(P\left( M \right) = \frac{3}{{10}} = 0,3.\)
Lời giải
Đáp số: \(362,9.\)
Thể tích của hộp sữa có dạng hình trụ là:
\(V = \pi {r^2}h \approx \pi \cdot 3,{8^2} \cdot 8 \approx 362,9{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Đoạn văn 1
II. PHẦN TỰ LUẬN (8,0 điểm, học sinh trình bày đầy đủ lời giải các bài từ bài 1 đến bài 4)
Câu 7-9. (1,5 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Câu 10-11. (2,0 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Câu 12-14. (2,5 điểm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Câu 15-16. (2,0 điểm) Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB,\,\,AC\) lần lượt tại \(B,C\) của \(\left( O \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 10/16 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập