Câu hỏi:
12/03/2025 308
Câu 12-14. (2,5 điểm)
1) Một thửa đất có dạng hình chữ nhật, chiều dài hơn chiều rộng 19 m và diện tích bằng \(150\,\,\;{{\rm{m}}^2}.\) Người ta dự định xây bức tường bao quanh thửa đất, xây theo chu vi của thửa đất, trừ 5 m của phần cổng. Biết giá tất cả các chi phí xây bức tường được tính với mỗi mét theo chu vi là 2 triệu đồng. Tính số tiền dự định xây bức tường đó.
Câu 12-14. (2,5 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x{\rm{\;(m)}}\) là chiều rộng của thửa đất hình chữ nhật \(\left( {x > 0} \right)\).
Chiều dài của thửa đất hình chữ nhật đó là \(x + 19{\rm{\;(m)}}{\rm{.}}\)
Diện tích của thửa đất hình chữ nhật đó là: \(x\left( {x + 19} \right){\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Theo bài, diện tích thửa đất bằng \(150\,\,\;{{\rm{m}}^2}\) nên ta có phương trình: \(x\left( {x + 19} \right) = 150\)
Giải phương trình:
\(x\left( {x + 19} \right) = 150\)
\({x^2} + 19x - 150 = 0\)
\({x^2} - 6x + 25x - 150 = 0\)
\(x\left( {x - 6} \right) + 25\left( {x - 6} \right) = 0\)
\(\left( {x - 6} \right)\left( {x + 25} \right) = 0\)
\(x - 6 = 0\) hoặc \(x + 25 = 0\)
\(x = 6\) (thỏa mãn) hoặc \(x = - 25\) (không thỏa mãn).
Như vậy, chiều rộng của thửa đất là \(6{\rm{\;m}}\) và chiều dài của thửa đất là \(6 + 19 = 25{\rm{\;(m)}}{\rm{.}}\)
Số mét tường cần xây là: \(2 \cdot \left( {6 + 25} \right) - 5 = 57{\rm{\;(m)}}{\rm{.}}\)
Số tiền dư định xây bức tường đó là: \(57 \cdot 2 = 114\) (triệu đồng).
Câu hỏi cùng đoạn
Câu 2:
2) Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{{\sqrt x }}{{\sqrt x + 1}} - \frac{2}{{x - 1}}\) (với \(0 \le x \ne 1).\)
Lời giải của GV VietJack
⦁ Với \(x \ge 0,\,\,x \ne 1,\) ta có:
\[P = \frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{{\sqrt x }}{{\sqrt x + 1}} - \frac{2}{{x - 1}}\]
\[ = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} - \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{x + \sqrt x - \left( {x - \sqrt x } \right) - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]\[ = \frac{{x + \sqrt x - x + \sqrt x - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{2\sqrt x - 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{2\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{2}{{\sqrt x + 1}}.\]
Như vậy, với \(x \ge 0,\,\,x \ne 1\) thì \[P = \frac{2}{{\sqrt x + 1}}.\]
⦁ Với \(x \ge 0,\,\,x \ne 1,\) ta có: \(\sqrt x + 1 > 0\) nên \(\frac{2}{{\sqrt x + 1}} > 0\) tức là \(P > 0.\)
Với \(x \ge 0,\,\,x \ne 1,\) ta cũng có \(\sqrt x + 1 \ge 1\) nên \(\frac{2}{{\sqrt x + 1}} \le 2\) tức là \(P \le 2.\)
Do đó, ta có \(0 < P \le 2.\)
Để \(P\) nhận giá trị nguyên thì \(P \in \left\{ {1;\,\,2} \right\}.\)
Với \(P = 1,\) ta có \[\frac{2}{{\sqrt x + 1}} = 1,\] suy ra \(\sqrt x + 1 = 2\) do đó \(\sqrt x = 1,\) nên \(x = 1\) (không thỏa mãn).
Với \(P = 2,\) ta có \[\frac{2}{{\sqrt x + 1}} = 2,\] suy ra \(\sqrt x + 1 = 1\) do đó \(\sqrt x = 0,\) nên \(x = 0\) (thỏa mãn).
Vậy \(x = 0\) thì \(P\) nhận giá trị nguyên.
Câu 3:
3) Tháp nghiêng ở thành phố Pisa, Italia nghiêng khoảng \(4^\circ \) so với phương thẳng đứng. Người ta gắn ở mặt ngoài của tháp hai thiết bị tại hai vị trí \(A,\,\,B\) và nối với nhau bởi dây truyền tín hiệu. Tính gần đúng độ dài nhỏ nhất của dây đó, biết \(HB\) gần bằng \(3,146\,\,\;{\rm{m,}}\) với \(H\) là hình chiếu vuông góc của \(A\) trên mặt đất (xem hình trên). Kết quả làm tròn đến hàng phần trăm.
Lời giải của GV VietJack
Độ dài dây \(AB\) nhỏ nhất khi \(A\) và \(B\) có vị trí như hình vẽ.
Xét \(\Delta ABH\) vuông tại \(H\), ta có: \[HB = AB \cdot \sin \widehat {BAH}\]
Suy ra \[AB = \frac{{HB}}{{\sin \widehat {BAH}}} \approx \frac{{3,146}}{{\sin 4^\circ }} \approx 45,10{\rm{\;(m)}}{\rm{.}}\]
Vậy độ dài dây \(AB\) nhỏ nhất khoảng \(45,10{\rm{\;m}}.\)
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
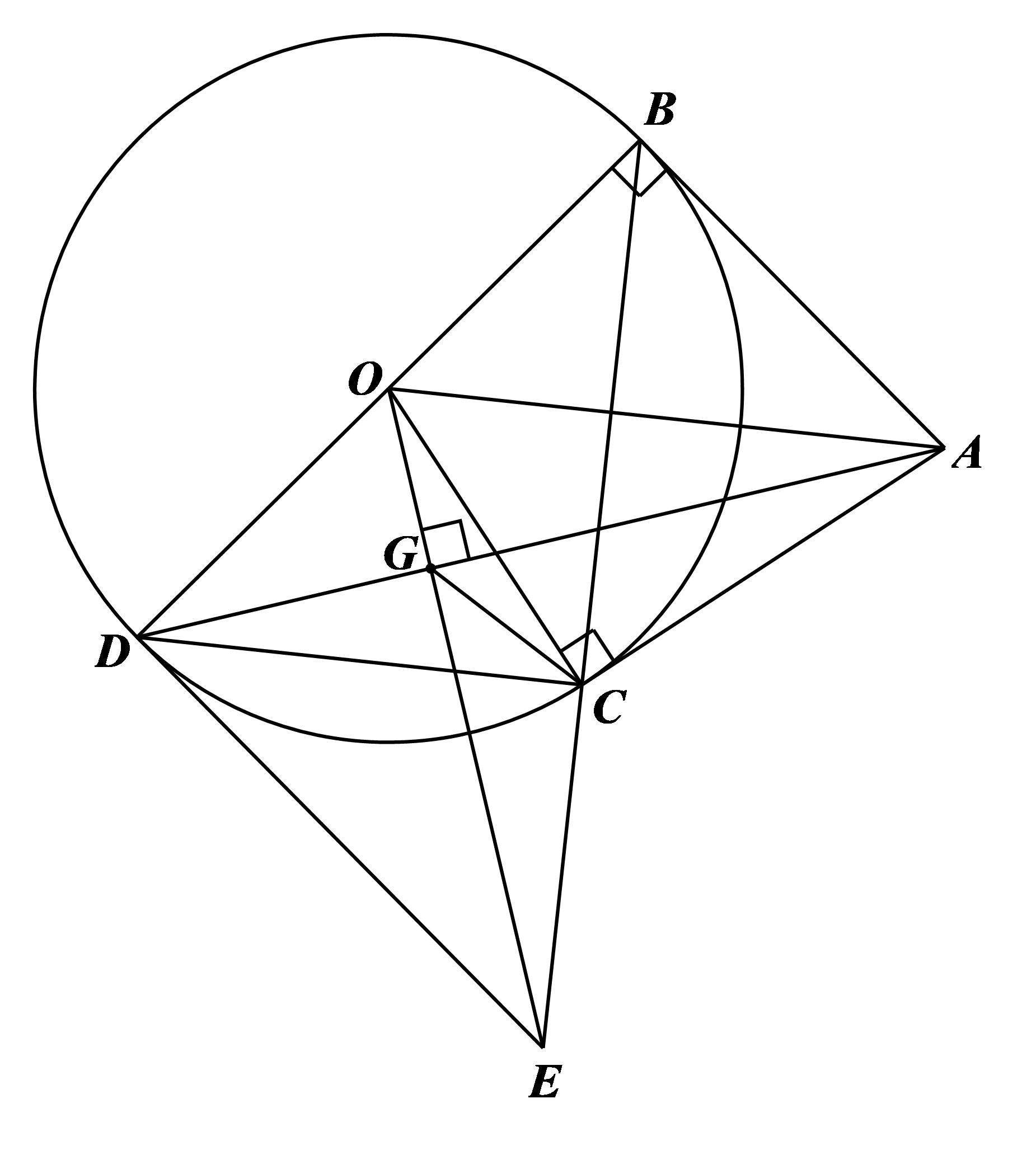
Vì \(AB,\,\,AC\) lần lượt là hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B,C\) nên \(AB \bot OB,\,\,AC \bot OC.\)
Do \(\Delta OAB\) vuông tại \(B\) nên đường tròn ngoại tiếp tam giác \(\Delta OAB\) có tâm là trung điểm của cạnh huyền \(OA.\) Tức là ba điểm \(O,\,\,A,\,\,B\) cùng thuộc đường tròn đường kính \(OA.\)
Chứng minh tương tự đối với \(\Delta OAC\) vuông tại \(C\) ta có ba điểm \(O,\,\,A,\,\,C\) cùng thuộc đường tròn đường kính \(OA.\)Vậy tứ giác \(ABOC\) nội tiếp đường tròn đường kính \(OA.\)
Lời giải
Tổng số chữ cái trong câu “Học hành vất vả kết quả ngọt bùi” là \(n = 35.\)
Số lần xuất hiện của các chữ cái \[b,\,\,n,\,\,o,\,\,t,\,\,v\] tương ứng là \[{m_1} = 1,\,\,{m_2} = 4,\,\,{m_3} = 3,\,\,\]\[{m_4} = 3,\,\,{m_5} = 3.\] Do đó các tần số tương đối cho các chữ cái \[b,\,\,n,\,\,o,\,\,t,\,\,v\] lần lượt là:
\[{f_1} = \frac{1}{{35}} \cdot 100\% \approx 2,86\% ,\,\,{f_1} = \frac{4}{{35}} \cdot 100\% \approx 11,43\% ,\,\,{f_3} = {f_4} = {f_5} = \frac{3}{{35}} \cdot 100\% \approx 8,57\% .\]
Ta có bảng tần số tương đối sau:
|
Chữ cái |
\[b\] |
\[n\] |
\[o\] |
\[t\] |
\[v\] |
|
Tần số tương đối |
\[2,86\% \] |
\[11,43\% \] |
\[8,57\% \] |
\[8,57\% \] |
\[8,57\% \] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận