1. Cho phương trình: \({x^2} - 8x + m - 1 = 0\) (m là tham số). Tìm giá trị của m để phương trình có hai nghiệm \({x_1},\,{x_2}\) sao cho biểu thức \[P = (x_1^2 - 1)(x_2^2 - 1) + 2087\] đạt giá trị nhỏ nhất.
2. Một đội xe dự định chở 120 tấn xi măng vào công trường. Khi chuẩn bị khởi hành thì đội xe được bổ sung thêm 5 chiếc xe nữa, nên cả đội đã chở thêm được 5 tấn và mỗi xe chở ít hơn so với dự định là 1 tấn xi măng. Hỏi theo dự định đội xe có bao nhiêu chiếc xe? Biết khối lượng xi măng mỗi xe chở là như nhau và mỗi xe chỉ chở đúng một chuyến.
1. Cho phương trình: \({x^2} - 8x + m - 1 = 0\) (m là tham số). Tìm giá trị của m để phương trình có hai nghiệm \({x_1},\,{x_2}\) sao cho biểu thức \[P = (x_1^2 - 1)(x_2^2 - 1) + 2087\] đạt giá trị nhỏ nhất.
2. Một đội xe dự định chở 120 tấn xi măng vào công trường. Khi chuẩn bị khởi hành thì đội xe được bổ sung thêm 5 chiếc xe nữa, nên cả đội đã chở thêm được 5 tấn và mỗi xe chở ít hơn so với dự định là 1 tấn xi măng. Hỏi theo dự định đội xe có bao nhiêu chiếc xe? Biết khối lượng xi măng mỗi xe chở là như nhau và mỗi xe chỉ chở đúng một chuyến.
Quảng cáo
Trả lời:
Giải bởi Vietjack
1)\({\Delta ^'} = 16 - (m - 1) = 17 - m\)
Phương trình đã cho có hai nghiệm khi và chỉ khi \({\Delta ^'} \ge 0 \Leftrightarrow m \le 17\)
Áp dụng hệ thức Viet, ta có: \({x_1} + {x_2} = 8;{\rm{ }}{x_1}{x_2} = m - 1\)
\[P = {({x_1}{x_2})^2} - {x_1}^2 - {x_2}^2 + 2088 = {({x_1}{x_2})^2} - {({x_1} + {x_2})^2} + 2{x_1}{x_2} + 2088\]
\[ = {(m - 1)^2} - {8^2} + 2(m - 1) + 2088 = {m^2} + 2023 \ge 2023\].
Dấu "=" xảy ra khi và chỉ khi \(m = 0\,\,(TM)\)
2)Gọi số chiếc xe ban đầu của đội xe là \[x\] (\(x \in {N^*}\))
½ Số tấn xi măng mỗi xe phải chở theo dự định là: \(\frac{{120}}{x}\) (tấn).
Lập được phương trình: \(\frac{{120}}{x} = \frac{{125}}{{x + 5}} + 1\)
Giải phương trình tìm được \({x_1} = 20\,\,(TM);{\rm{ }}{x_2} = - 30\,\,(KTM)\)
KL: …
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1.\(\sqrt {x - 2} \) có nghĩa khi \(x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
2.\(\sqrt {36} + \sqrt 9 = 6 + 3 = 9\)
3a. Tìm được \(x = 2\)
b)Tìm đúng 2 nghiệm \({x_1} = 1;\,{x_2} = - 3\)
4a)Xác định được 2 điểm thuộc đồ thị.
Vẽ đúng đồ thị:
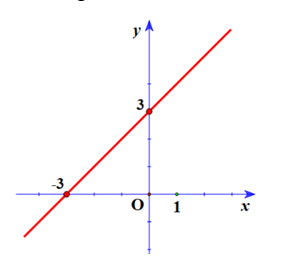
b)\[(d'):\,\,y = 2x + m - 1\] cắt đường thẳng \((d)\) tại một điểm trên trục tung
\( \Leftrightarrow m - 1 = 3 \Leftrightarrow m = 4\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập