Cho nửa đường tròn tâm \(O\), đường kính \(BC\). Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(A\) (\(A\) khác \(B\) và \(C)\), gọi \(H\) là hình chiếu của \(A\) trên \(BC\). Trên cung \(AC\) của nửa đường tròn \(\left( O \right)\) lấy điểm \(D\) (\(D\) khác \(A\) và \(C\)), gọi \(E\) là hình chiếu của \(A\) trên \(BD,\) \(I\)là giao điểm của hai đường thẳng \(AH\) và \(BD\).
a) Chứng minh tứ giác \(ABHE\) nội tiếp;
b) Chứng minh \(BI \cdot BD = BH \cdot BC\);
c) Chứng minh hai tam giác \(AHE\) và \(ACD\) đồng dạng;
d) Hai đường thẳng \(AE\) và \(DH\) cắt nhau tại \(F\). Chứng minh \(IF{\rm{//}}AD\).
Cho nửa đường tròn tâm \(O\), đường kính \(BC\). Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(A\) (\(A\) khác \(B\) và \(C)\), gọi \(H\) là hình chiếu của \(A\) trên \(BC\). Trên cung \(AC\) của nửa đường tròn \(\left( O \right)\) lấy điểm \(D\) (\(D\) khác \(A\) và \(C\)), gọi \(E\) là hình chiếu của \(A\) trên \(BD,\) \(I\)là giao điểm của hai đường thẳng \(AH\) và \(BD\).
a) Chứng minh tứ giác \(ABHE\) nội tiếp;
b) Chứng minh \(BI \cdot BD = BH \cdot BC\);
c) Chứng minh hai tam giác \(AHE\) và \(ACD\) đồng dạng;
d) Hai đường thẳng \(AE\) và \(DH\) cắt nhau tại \(F\). Chứng minh \(IF{\rm{//}}AD\).
Quảng cáo
Trả lời:
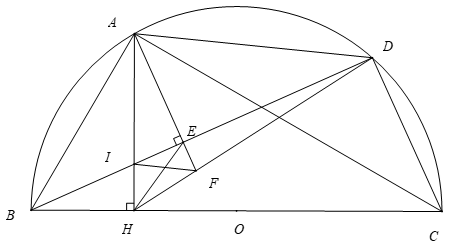
a) Do \[AH \bot BC\left( {gt} \right);AE \bot BD\left( {gt} \right) \Rightarrow \widehat {AHB} = \widehat {AEB} = 90^\circ \]
Mà \({\rm{E}},{\rm{H}}\) là hai đỉnh kề nhau, cùng nhìn \({\rm{AD}}\) dưới 2 góc bằng nhau nên \({\rm{A}},{\rm{E}},{\rm{H}},{\rm{B}}\) cùng thuộc một đường tròn.
Hay tứ giác \(ABHE\) nội tiếp (đpcm)
b) Ta có \(\widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BIH\) và \(\Delta BCD\) có:
\(\widehat {CBD}\) chung;
\[\widehat {BHI} = \widehat {BDC} = 90^\circ \]
\( \Rightarrow BI \cdot BD = BH \cdot BC\) (đpcm)
c) Do \(ABHE\) nội tiếp (cmt) nên \(\widehat {AHE} = \widehat {ABE}\) (hai góc nội tiếp cùng chắn cung \({\rm{AE}}\) )
Mà \(\widehat {ABE} = \widehat {ACD}\) (hai góc nội tiếp cùng chắn cung \({\rm{AD}}\) )
\( \Rightarrow \widehat {AHE} = \widehat {ACD}\).
Do \(ABHE\) nội tiếp (cmt) nên \(\widehat {HAE = }\widehat {HBE} = \widehat {CBD}\) (hai góc nội tiếp cùng chắn cung HE)
Lại có tứ giác \({\rm{ABCD}}\) nội tiếp \(\left( O \right) \Rightarrow \widehat {CBD} = \widehat {CAD}\) (hai góc nội tiếp cùng chắn cung \({\rm{CD}}\))
\( \Rightarrow \widehat {HAE} = \widehat {CAD}\)
Xét tam giác \({\rm{AHE}}\) và tam giác \({\rm{ACD}}\) có:
\[\widehat {AHE} = \widehat {ACD}\left( {{\rm{cmt}}} \right)\]
\[\widehat {HAE} = \widehat {CAD}\left( {{\rm{cmt}}} \right)\]
\[ \Rightarrow \Delta AEH \sim \Delta \Delta ADC\left( {g \cdot g} \right)\] \[\begin{array}{*{20}{r}}{}&{}\\{}&{}\\{}&\;\end{array}\]
d) Hai đường thẳng \(AE\) và \(DH\) cắt nhau tại \(F\). Chứng minh \(IF{\rm{//}}AD\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Khi \(m = 3\) phương trình trở thành: \({x^2} - 8x - 9 = 0\),
ta có: \({\rm{\Delta '}} = {( - 4)^2} - 1 \cdot \left( { - 9} \right) = 25 > 0\)
Suy ra phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{4 + \sqrt {25} }}{1} = 9;{x_2} = \frac{{4 - \sqrt {25} }}{1} = - 1\)
Vậy với \(m = 3\) phương trình có hai nghiệm phân biệt \({x_1} = 9;{x_2} = - 1\)
b) \(ac = 1.\left( { - 9} \right) < 0\) nên phương trình luôn có hai nghiệm phân biệt.
Phương trình có nghiệm \(x = 2\) nên thay \(x = 2\) vào phương trình ta có:
\(\begin{array}{l}{2^2} - 2\left( {m + 1} \right)2 - 9 = 0 \Leftrightarrow 4 - 4m - 4 - 9 = 0\\ \Leftrightarrow - 4m - 9 = 0\\ \Leftrightarrow m = - \frac{9}{4}\end{array}\)
Vậy để phương trình có nghiệm \(x = 2\) thì \(m = - \frac{9}{4}\).
c) Xét phương trình \({x^2} - 2\left( {m + 1} \right)x - 9 = 0\) có \(a \cdot c = - 9 < 0\) nên phương trình luôn có 2 nghiệm trái dấu \({x_1},{x_2}\)
Áp dụng hệ thức viet ta có \({x_1} + {x_2} = 2\left( {m + 1} \right)\)
Mà \({x_1} < {x_2} \Rightarrow {x_1} < 0 < {x_2}\)
\(\left| {{x_1}} \right| - \left| {{x_2}} \right| = - 6\)
\( - {x_1} - {x_2} = - 6\)
\( \Leftrightarrow \)\( - \left( {{x_1} + {x_2}} \right) = - 6\)
\( \Leftrightarrow m + 1 = 3\)
\( \Leftrightarrow {x_1} + {x_2} = 6\)
Lời giải
Gọi cạnh hình lập phương bằng \(x\left( {{\rm{dm}}} \right)\). ĐK:
Gọi chiều cao bằng chiều rộng là ĐK: .
Chiều dài hình hộp chữ nhật bằng .
Hình lập phương có 12 cạnh có độ dài bằng .
Hình hộp chữ nhật có 8 cạnh có độ dài bằng và 4 cạnh có độ dài .
Người thợ cắt vừa đủ một cây sắt dài nên ta có:
\({\rm{x}} > 0\)
Thể tích khối lập phương là \({V_1} = {x^3}\).
Thể tích khối hộp chữ nhật là \({V_2} = y \cdot y \cdot 6y = 6{y^3}\).
Tổng thể tích hai hình là: \(V = {V_1} + {V_2} = {x^3} + 6{y^3} = {\left( {\frac{{25 - 8y}}{3}} \right)^3} + 6{y^3}\).
\(12x + 8y + 4.6y = 100 \Leftrightarrow 12x + 32y = 100 \Leftrightarrow 3x + 8y = 25 \Leftrightarrow x = \frac{{25 - 8y}}{3}\)
Ta có: \({x^3} + {3^3} + {3^3} \ge 3\sqrt[3]{{{x^3} \cdot {3^3} \cdot {3^3}}} = 27x\)
\(6\left( {{y^3} + {2^3} + {2^3}} \right) \ge 6 \cdot 3 \cdot \sqrt[3]{{{y^3} \cdot {2^3} \cdot {2^3}}} = 72y\)
Cộng vế theo vế hai bất đẳng thức ta được:
\({x^3} + 6{y^3} + 150 \ge 27x + 72y\)
\( \Leftrightarrow V + 150 \ge 9\left( {3x + 8y} \right)\)
\( \Leftrightarrow V + 150 \ge 9.25\)
\( \Leftrightarrow V + 150 \ge 225\)
\( \Leftrightarrow V \ge 75\)
Dấu "=" xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 2}\end{array}} \right.\).
Vậy tổng thể tích của hai hình thu được nhỏ nhất bằng \(75{\rm{d}}{{\rm{m}}^3}\) khi độ dài cạnh hình lập phương bằng \(3{\rm{dm}}\), độ dài chiều rộng và chiều cao hình hộp chữ nhật bằng \(2{\rm{dm}}\), chiều dài hình hộp chữ nhật bằng \(12{\rm{dm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.