khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Ôn vào 10
  3. Toán

Câu hỏi:

12/03/2026 4,166 Lưu

(2,5 điểm)
Một người mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là \[850\] nghìn đồng. Khi trả tiền người đó được khuyến mại giảm \[20\% \] đối với giá tiền bàn là và \[10\% \] đối với giá tiền quạt điện với giá niêm yết. Vì vậy, người đó phải trả tổng cộng \[740\] nghìn đồng. Tính giá tiền của cái bàn là và cái quạt điện theo giá niêm yết

Xem lời giải

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 35 !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Gọi giá tiền của bàn là và quạt điện theo giá niêm yết lần lượt là: \(x;\,y\) (đơn vị: nghìn đồng; điều kiện \(0 < x;\,y < 850\)).

Do tổng số tiền mua bàn là và quạt điện theo giá niêm yết là \[850\] nghìn đồng nên ta có phương trình:  \(x + y = 850\)   (1).

Bàn là giảm giá 20% nên số tiền cần trả cho bàn là là: \(x - \frac{{20}}{{100}}x = \frac{4}{5}x\) (nghìn đồng).

Quạt điện giảm giá 10% nên số tiền trả cho quạt điện là: \(y - \frac{{10}}{{100}}y = \frac{9}{{10}}y\) (nghìn đồng).

Tổng số tiền phải trả theo giá khuyến mại là \[740\] nghìn nên ta có phương trình:

\(\frac{4}{5}x + \frac{9}{{10}}y = 740\)     (2)

        Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y = 850\,\,\,\,\,\,\,\,\,\,}\\{\frac{4}{5}x + \frac{9}{{10}}y = 740}\end{array}} \right.\)

        Giải hệ ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 250}\\{y = 500}\end{array}} \right.\) (thỏa mãn điều kiện)

        Vậy giá tiền của bàn là là \[250\] nghìn đồng, của quạt điện là \[600\] nghìn đồng.

Câu hỏi cùng đoạn

Câu 2:

Một người đi xe đạp từ địa điểm \[A\] đến địa điểm \[B\] với vận tốc không đổi, hai địa điểm cách nhau \(30\,km\). Khi đi từ \[B\] về \[A\], người đó chọn đường khác dễ hơn nhưng dài hơn con đường cũ \(6\,km\). Vì lúc về, người đó đi với vận tốc lớn hơn vận tốc lúc đi là \(3\,km/h\) nên thời gian về vẫn ít hơn thời gian đi là \(20\) phút. Tính vận tốc lúc đi của người đó.

Xem lời giải

verified Giải bởi Vietjack

Gọi vận tốc lúc đi là: \(x\,\)(km/h) \(\left( {x > 0} \right)\)

      Thời gian lúc đi là \(\frac{{30}}{x}\) (giờ)

      Quãng đường lúc về là : \(30 + 6 = 36\) (km)

      Vận tốc lúc về là : \(x + 3\) (km/h)

      Thời gian lúc về là : \(\frac{{36}}{{x + 3}}\) (giờ)

Theo đầu bài thời gian về ít hơn thời gian đi \(20\) phút = \(\frac{1}{3}\) giờ nên ta có phương trình:

\(\frac{{30}}{x} - \frac{{36}}{{x + 3}} = \frac{1}{3}\)

                                                   \(\frac{{90\left( {x + 3} \right)}}{{3x\left( {x + 3} \right)}} - \frac{{108x}}{{3x\left( {x + 3} \right)}} = \frac{{x\left( {x + 3} \right)}}{{3x\left( {x + 3} \right)}}\)

                                                           \(90\left( {x + 3} \right) - 108x = x\left( {x + 3} \right)\)

                                                              \({x^2} + 21x - 270 = 0\)

                                                             \(\left( {x + 30} \right)\left( {x - 9} \right) = 0\)

                                                         \(x =  - 30\) (loại) hoặc \(x = 9\) (thoả mãn)

            Vậy vận tốc lúc đi là \(9\) km/h.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta đặt một khối nón vào trong một khối lập phương cạnh \(1\,m\) chứa đầy nước. Biết rằng đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính thể tích lượng nước trong khối bị tràn ra ngoài. (Lấy \(\pi  \approx 3,14,\) kết quả làm tròn đến hai chữ số thập phân)

Media VietJack

Lời giải

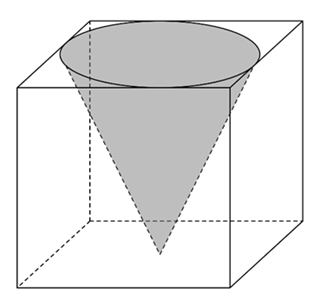
Thể tích lượng nước trong khối hộp bị tràn ra ngoài là thể tích của khối nón.

\(V = \frac{1}{3}\pi {R^2}h \approx \frac{1}{3} \cdot 3,14.{\left( {\frac{1}{2}} \right)^2} \cdot 1 \approx 0,26\,\,\,({m^2})\)

      Vậy lượng nước bị trào ra có thể tích \( \approx 0,26\,\,\,({m^2})\).

Câu 2

Biểu đồ bên biểu diễn tỉ lệ đại biểu tham dự hội nghị theo độ tuổi. Biết rằng có 54 đại biểu từ 25 tuổi đến 35 tuổi.

Media VietJack 

a) Có bao nhiêu đại biểu tham dự hội nghị?

b) Một người cho rằng có trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi. Nhận định đó đúng hay sai? Tại sao?

Lời giải

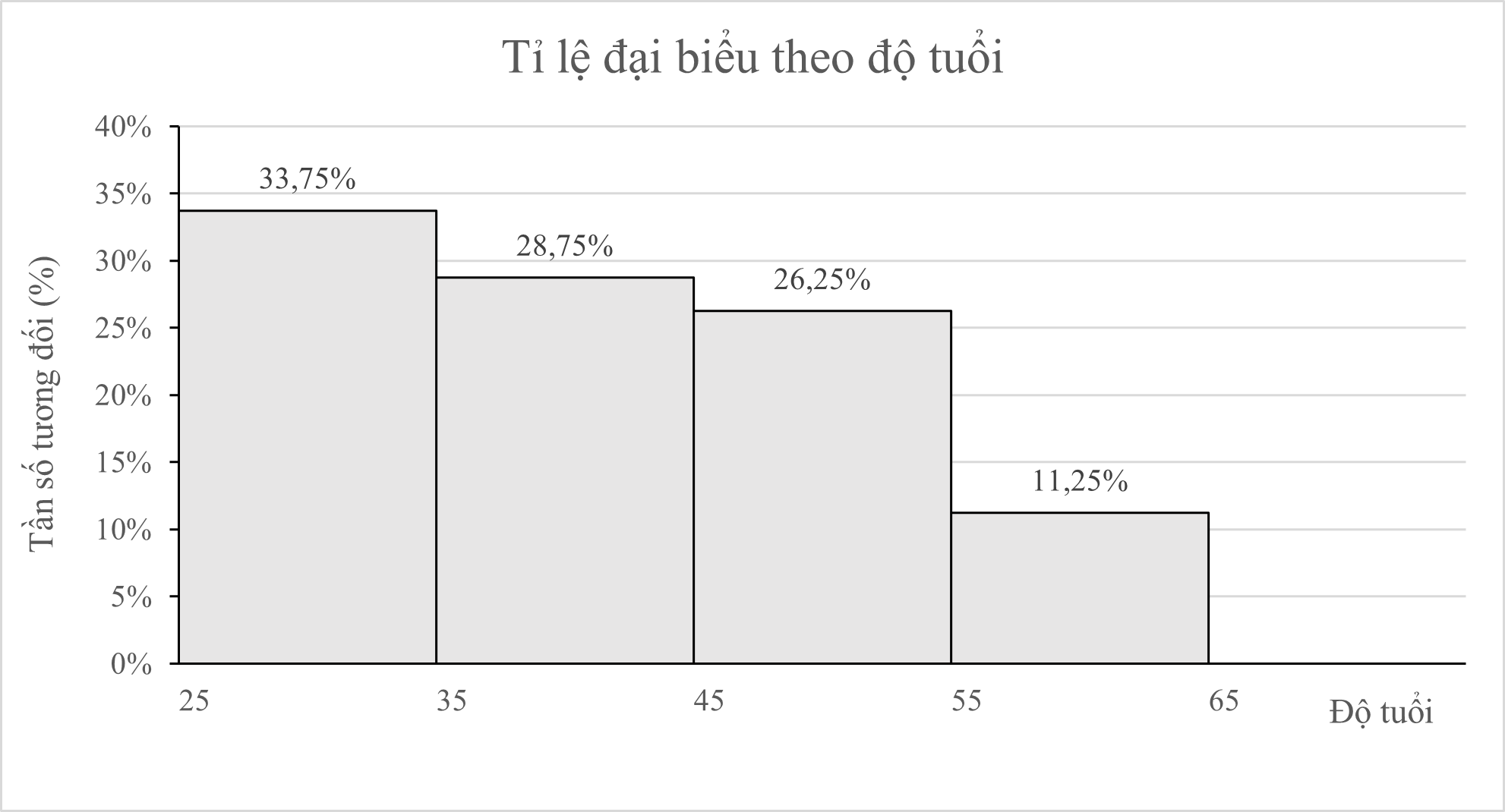
a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.

Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)

Vậy tổng số đại biểu tham dự hội nghị là 160 người.

b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:

\[33,75\%  + 28,75\%  = 62,5\%  > 50\% .\]

Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.

Câu 3

(0,5 điểm)   Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
Media VietJack

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

(1,5 điểm)  Cho hai biểu thức: \(A = \frac{{\sqrt x  + 1}}{{\sqrt x  + 3}}\) ; \(B = \frac{{2\sqrt x }}{{\sqrt x  + 1}} - \frac{{\sqrt x  + 2}}{{\sqrt x  - 1}} + \frac{{2\sqrt x  + 4}}{{x - 1}}\) với \(x \ge 0;x \ne 1\)

                        a) Tính giá trị của \[A\] khi \[x = 4.\]                       

                        b) Rút gọn \[B\]

                        c) Tìm \[x\] để \(A.B \le \frac{1}{2}\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia thành \(12\) phần bằng nhau và ghi các số \(1;2;3;...;12\). Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

 Media VietJack

Xét phép thử: “Quay đĩa tròn một lần” và biến cố \(P:\) “Chiếc kim chỉ vào hình quạt ghi số là số nguyên tố”. Tính xác suất của biến cố \(P\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một người đi xe đạp từ địa điểm \[A\] đến địa điểm \[B\] với vận tốc không đổi, hai địa điểm cách nhau \(30\,km\). Khi đi từ \[B\] về \[A\], người đó chọn đường khác dễ hơn nhưng dài hơn con đường cũ \(6\,km\). Vì lúc về, người đó đi với vận tốc lớn hơn vận tốc lúc đi là \(3\,km/h\) nên thời gian về vẫn ít hơn thời gian đi là \(20\) phút. Tính vận tốc lúc đi của người đó.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập