Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 6 !!
Quảng cáo
Trả lời:
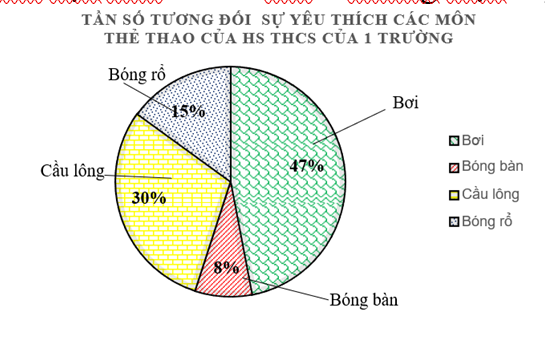
Bảng tần số tương đối của biểu đồ trên là:
|
Môn thể thao được yêu thích |
Bơi |
Bóng bàn |
Cầu lông |
Bóng rổ |
|
Tần số tương đối |
\(47\% \) |
\(8\% \) |
\(30\% \) |
\(15\% \) |
Môn thể thao nào được học sinh THCS của \(1\) trường yêu thích nhất là môn bơi vì môn bơi chiếm \(47\% \) các bạn yêu thích.
Câu hỏi cùng đoạn
Câu 2:
Hình vẽ dưới đây mô tả một đĩa tròn bằng bìa cứng được chia làm mười phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Xét phép thử “Quay đĩa tròn một lần” và biến cố A: “ Mũi tên chỉ vào hình quạt ghi số là số nguyên tố”. Tính xác suất của biến cố A.
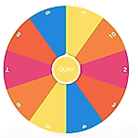

Không gian mẫu của phép thử là
\[\Omega = \left\{ {1;{\rm{ }}2;{\rm{ }}3;{\rm{ }}4;{\rm{ }}5; \ldots ..;{\rm{ 10}}} \right\}\].
Không gian mẫu có 10 phần tử.
Vì các phần của đĩa tròn giống nhau nên các kết quả của phép thử là đồng khả năng.
Có 4 kết quả thuận lợi cho biến cố A là \[2;\,3;\,5;\,7\]. Xác suất của biến cố A là \(P\left( A \right) = \frac{4}{{10}} = \frac{2}{5}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số tiền cô Linh đầu tư cho khoản thứ nhất và thứ hai lần lượt là \(x;y\) (triệu đồng, \(0 < x;y < 500\))
Theo đề bài ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 500\\5\% .x + 6\% .y = 28\end{array} \right.\)
Giải được \(\left\{ \begin{array}{l}x = 200\\y = 300\end{array} \right.\left( {tm} \right)\)
Vậy cô Linh đầu tư \(200\) triệu vào khoản thứ nhất và \(300\) triệu vào khoản thứ hai.
Lời giải
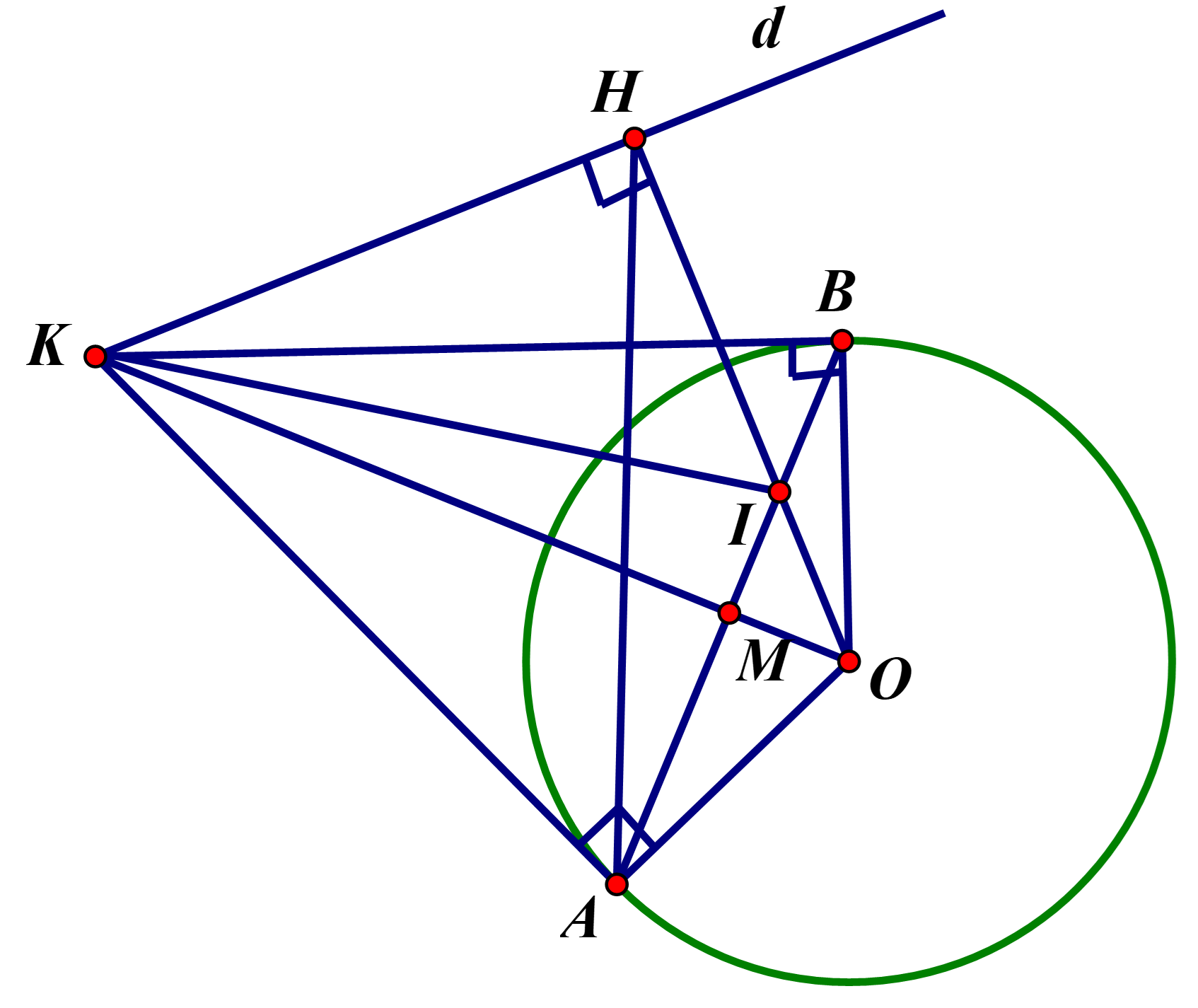
a) = 900( vì KA là tiếp tuyến của (O) (gt))
= 900( )
Suy ra tam giác KAO vuông tại A, tam giác KHO vuông tại H
Nên A, H thuộc đường tròn đường kính OK
Vậy tứ giác \(KAOH\) nội tiếp được trong đường tròn.
b) Các đỉnh \(H,B,A\) cùng nhìn cạnh \(OK\) dưới một góc vuông
nên năm điểm \(K,A,B,O,H\) cùng thuộc đường tròn đường kính \(OK\) suy ra \(\widehat {AHI} = \widehat {ABO}\) (hai góc nội tiếp cùng chắn cung \(AO\)).
Xét tam giác \(IAH\) và tam giác \(IOB\) có:
\(\widehat {HIA} = \widehat {BIO}\) (đối đỉnh)
và \(\widehat {AHI} = \widehat {ABO}\) ( cmt ).
Do đó .
c) Gọi \(M\) là giao điểm của OK và AB
Theo tính chất tiếp tuyến ta có KA=KB;
Lại có \(OA = OB = R\) nên OK là đường trung trực của AB, suy ra \(AB \bot OK\) tại \(M\) và \(MA = MB\).
Ta có: \(\Delta OMI \sim \Delta OHK\;(g.g)\) suy ra \(OI = \frac{{OK.OM}}{{OH}} = \frac{{O{A^2}}}{{OH}} = \frac{{{R^2}}}{{OH}} = \frac{{{R^2}}}{{R\sqrt 3 }} = \frac{R}{{\sqrt 3 }}\).
Xét \(\Delta OAK\) vuông tại \(A\), có \(O{A^2} = OM \cdot OK \Leftrightarrow OM = \frac{{O{A^2}}}{{OK}} = \frac{{{R^2}}}{{2R}} = \frac{R}{2}\)
Suy ra \(KM = OK - OM = 2R - \frac{R}{2} = \frac{{3R}}{2}\)
\(A{M^2} = OM \cdot KM = \frac{R}{2} \cdot \frac{{3R}}{2} = \frac{{3{R^2}}}{4} \Rightarrow AM = \frac{{R\sqrt 3 }}{2}\)
Xét \(\Delta OMI\) vuông tại \(M\), có \(MI = \sqrt {O{I^2} - O{M^2}} = \sqrt {{{\left( {\frac{R}{{\sqrt 3 }}} \right)}^2} - {{\left( {\frac{R}{2}} \right)}^2}} = \frac{{R\sqrt 3 }}{6}\)
Suy ra \(AI = AM + MI = \frac{{R\sqrt 3 }}{2} + \frac{{R\sqrt 3 }}{6} = \frac{{2R\sqrt 3 }}{3}\)
Diện tích \(\Delta AKI\) là \(S = \frac{1}{2}AI \cdot KM = \frac{1}{2} \cdot \frac{{3R}}{2} \cdot \frac{{2R\sqrt 3 }}{3} = \frac{{{R^2}\sqrt 3 }}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.