Cho biểu thức \(A = \left( {\frac{{x + 4\sqrt x + 4}}{{x + \sqrt x - 2}} + \frac{{x + \sqrt x }}{{1 - x}}} \right):\left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{1 - \sqrt x }}} \right)\) ( với \(x > 0;\,x \ne 1\))
a) Rút gọn biểu thức \(A\)
b) Có bao nhiêu giá trị nguyên của \(x\) để \(A \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }}\)
Cho biểu thức \(A = \left( {\frac{{x + 4\sqrt x + 4}}{{x + \sqrt x - 2}} + \frac{{x + \sqrt x }}{{1 - x}}} \right):\left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{1 - \sqrt x }}} \right)\) ( với \(x > 0;\,x \ne 1\))
a) Rút gọn biểu thức \(A\)
b) Có bao nhiêu giá trị nguyên của \(x\) để \(A \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }}\)
Quảng cáo
Trả lời:
a) \(A = \left( {\frac{{x + 4\sqrt x + 4}}{{x + \sqrt x - 2}} + \frac{{x + \sqrt x }}{{1 - x}}} \right):\left( {\frac{1}{{\sqrt x + 1}} - \frac{1}{{1 - \sqrt x }}} \right)\)
\(\)\( = \left[ {\frac{{{{\left( {\sqrt x + 2} \right)}^2}}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}} + \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}}} \right]:\frac{{\sqrt x - 1 + \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \left[ {\frac{{\sqrt x + 2}}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{1 - \sqrt x }}} \right]:\frac{{2\sqrt x }}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}}\)
\( = \frac{2}{{\sqrt x - 1}}.\frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}{{2\sqrt x }} = \frac{{\sqrt x + 1}}{{\sqrt x }}\)
Vậy \(A = \frac{{\sqrt x + 1}}{{\sqrt x }}\) với \(x > 0;\,x \ne 1\).
b) \(A \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \Leftrightarrow \frac{{\sqrt x + 1}}{{\sqrt x }} \ge \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \Leftrightarrow \frac{{\sqrt x + 1}}{{\sqrt x }} - \frac{{1 + \sqrt {2023} }}{{\sqrt {2023} }} \ge 0\)
\( \Leftrightarrow \frac{{\sqrt x \sqrt {2023} + \sqrt {2023} - \sqrt x - \sqrt x .\sqrt {2023} }}{{\sqrt x .\sqrt {2023} }} \ge 0 \Leftrightarrow \sqrt {2023} - \sqrt x \ge 0 \Leftrightarrow x \le 2023\)
Kết hợp điều kiện \(x > 0;\,x \ne 1\) ta có \(2022\) giá trị thỏa mãn điều kiện
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
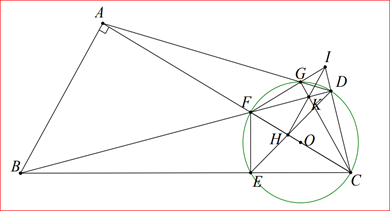
a) tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {BAC} = 90^\circ \) hay \(\widehat {BAF} = 90^\circ \)
ta có: \(FE \bot BC\) tại \(E\) nên \(\widehat {FEB} = \widehat {FEC} = 90^\circ \)
xét tứ giác \(ABEF\) có \(\widehat {BAF} + \widehat {FEB} = 180^\circ \) mà hai góc đối nhau nên \(ABEF\) là tứ giác nội tiếp
b) Xét đường tròn tâm \(\left( O \right)\) có \(\widehat {FDC} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn)
Hay \(\widehat {BDC} = 90^\circ \)
Xét tứ giác \(ABCD\) có \(\widehat {BAC} = \widehat {BDC} = 90^\circ \) mà hai đỉnh kề nên \(ABCD\) là tứ giác nội tiếp
Xét đường tròn ngoại tiếp tứ giác \(ABCD\) có \(\widehat {ABD} = \widehat {ACD}\) ( hai góc nội tiếp cùng chắn )
Hay \(\widehat {ABF} = \widehat {FCD}\) (1)
Xét đường tròn ngoại tiếp tứ giác \(ABEF\) có \[\widehat {ABF} = \widehat {AEF}\]( hai góc nội tiếp cùng chắn ) (2)
Xét đường tròn tâm \(\left( O \right)\) có \[\widehat {FCD} = \widehat {FED}\]( hai góc nội tiếp cùng chắn ) (3)
Từ (1); (2) và (3) ta có \[\widehat {FED} = \widehat {AEF}\] nên \(FE\) là tia phân giác của \(\widehat {AED}\)
Xét tam giác \(AEH\) có \[{\rm{EF;EC}}\] là đường phân giác trong và ngoài của tam giác nên \[\frac{{AF}}{{FH}} = \frac{{AE}}{{EH}};\frac{{AC}}{{CH}} = \frac{{AE}}{{EH}}\]
Suy ra \(\frac{{AF}}{{FH}} = \frac{{AC}}{{CH}} \Leftrightarrow AF.CH = FH.AC\)
c) Xét đường tròn \(\left( O \right)\) có \(\widehat {FGC} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn) suy ra \(CG \bot FI\)
Xét tam giác \[IFC\] có \(FD;CG\) là hai đường cao mà \(FD\) cắt \(CG\) tại \(K\) suy ra \(K\) là trực tâm
Suy ra \(IK \bot FC\)
Xét đường tròn \(\left( O \right)\) có \(\widehat {FDA} = \widehat {FCG}\) ( hai góc nội tiếp cùng chắn )
Mà \(\widehat {FDA} = \widehat {BCA}\) ( hai góc nội tiếp cùng chắn )
Do đó \(\widehat {BCA} = \widehat {FCG}\) hay \(\widehat {FCE} = \widehat {FCG}\)
Xét \(\Delta FEC\) và \(\Delta FGC\) có \(\widehat {FCE} = \widehat {FCG}\) và \(\widehat {FEC} = \widehat {FGC} = 90^\circ \)
Suy ra do đó
Xét đường tròn tâm \(\left( O \right)\) có
Suy ra \(\widehat {GFC} = \widehat {EDC}\) hay \(\widehat {IFH} = \widehat {HDC}\)
Xét tứ giác \(FHDI\) có \(\widehat {IFH} = \widehat {HDC}\) mà góc ngoài bằng góc trong đỉnh đối diện nên \(FHDI\) là tứ giác nội tiếp
Suy ra \(\widehat {FHI} = \widehat {FDI} = 90^\circ \Rightarrow IH \bot FC\)
Suy ra \(K;I;H\) thẳng hàng
Lời giải
Gọi d là đường thẳng trong \(2025\) đường thẳng thỏa mãn đề bài
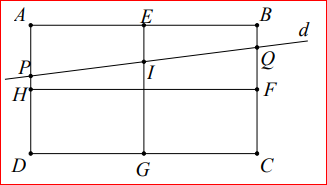
Giả sử d cắt \(AD;BC\) lần lượt tại \(P;Q\) và cắt \(EG\) tại \(I\)
\(E;F;G;H\) là trung điểm các cạnh như hình
Mà \({S_{DCQP}} = 2{S_{ABQP}} \Rightarrow \left( {DP + QC} \right) = 2\left( {AP + BQ} \right) \Leftrightarrow GI = 2IE \Leftrightarrow GI = \frac{2}{3}GE\) suy ra \(I\) cố định
Khi đó ta có \(2025 = 4.506 + 1\) các đường thẳng thỏa mãn đề bài phải đi qua 4 điểm cố định khi đó theo nguyên lý Dirichlet thì có \(506 + 1 = 507\) đường thẳng đi qua một điểm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.