Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Thư rủ nhau đi ăn kem ở một quán gần trường. Do quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem giảm 1 500 đồng so với giá ban đầu. Nhóm của Thư mua 9 ly kem với số tiền là 154 500 đồng. Hỏi giá của một ly kem ban đầu?
Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Thư rủ nhau đi ăn kem ở một quán gần trường. Do quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem giảm 1 500 đồng so với giá ban đầu. Nhóm của Thư mua 9 ly kem với số tiền là 154 500 đồng. Hỏi giá của một ly kem ban đầu?
Quảng cáo
Trả lời:
Gọi \[x\] (đồng) là giá ly kem ban đầu \[\left( {x > 0} \right)\].
Theo giả thiết ta có phương trình: \[4x + \left( {9 - 4} \right)\left( {x - 1\,500} \right) = 154\,500\]
\[ \Leftrightarrow 9x = 162\,000 \Leftrightarrow x = 18\,000\] (đồng).
Vậy giá tiền của một ly kem ban đầu là 18 000 đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
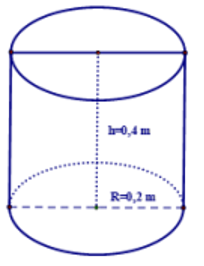
a) Thể tích 1 cái thùng hình trụ là
\[{V_{tru}} = \pi {R^2}h = \pi {.0,2^2}.0,4 \approx 0,05\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Lượng nước anh Minh đổ vào hồ trong mỗi lần gánh là
\[{V_g} = 2{V_{tru}}.90\% \approx 0,09\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Thể tích cái hồ là: \[V = 2.2.1 = 4\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có: \[4:0,09 \approx 44,44\]
Vậy anh Minh cần gánh ít nhất 45 lần để đầy hồ.
Lời giải

a)
Ta có:\[JM = JE\] (tính chất hai tiếp tuyến cắt nhau) và \[OM = OE\] (bán kính).
\[ \Rightarrow OJ\] là đường trung trực của \[ME\].
Từ đó suy ra \[\Delta OMJ = \Delta OEJ\] (c – c – c).
\[ \Rightarrow \widehat {MOF} = \widehat {EOF}\]
Từ đó suy ra \[\Delta OMF = \Delta OEF\] (c – g – c).
\[ \Rightarrow \widehat {OMF} = \widehat {OEF}\].
b)
Ta có \[\widehat {OMI} = \widehat {ODI} = 90^\circ \] (định nghĩa tiếp tuyến tại điểm).
Suy ra tứ giác \[ODIM\] nội tiếp (1).
Xét tam giác \[\Delta OED\] có \[\widehat {OED} = \widehat {ODE}\] (do \[OD = OE = R\])
Theo ý a) ta có \[\widehat {OMF} = \widehat {OEF}\] nên ta có \[\widehat {ODE} = \widehat {ODF} = \widehat {OMF}\]
Suy ra tứ giác \[ODMF\] nội tiếp (do cùng chắn cung \[OF\]) (2).
Từ (1) và (2) suy ra 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn.
c)
+) Ta có tứ giác\[IDOF\]nội tiếp (do 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn).
\[ \Rightarrow \widehat {DIO} = \widehat {DFO}\] (cùng chắn cung DO )
\[ \Rightarrow \widehat {AIO} = \widehat {EFO}\] (2 góc kề bù tương ứng) (3)
Ta lại có tứ giác \[ADOE\] nội tiếp (do \[\widehat {ADO} = \widehat {AEO} = 90^\circ \])
\[ \Rightarrow \widehat {DAO} = \widehat {DEO}\] (4)
Từ (3) và (4) suy ra (g – g).
\[ \Rightarrow \widehat {IOA} = \widehat {EOF}\]
Mà \[\widehat {EOF} = \widehat {JOM}\]
Nên \[\widehat {IOA} = \widehat {JOM}\].
+) Ta có \[\sin \widehat {IOA} = \sin \widehat {JOM} = \frac{{MJ}}{{OJ}}\] (5).
Mặt khác \[JMFO\] nội tiếp (do ý b) nên ta có \[\widehat {JMF} = \widehat {JOI}\].
Suy ra (g – g) \[ \Rightarrow \frac{{MJ}}{{JO}} = \frac{{MF}}{{OI}}\](6)
Từ (5) và (6) suy ra \[\sin \widehat {IOA} = \frac{{MF}}{{IO}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.