Theo quy định của cửa hàng xe máy, đề hoàn thành chỉ tiêu trong một tháng, mỗi nhân viên phải bán được trung bình một chiếc xe máy trong một ngày. Nhân viên nào hoàn thành chỉ tiêu trong một tháng thì nhận lương cơ bản là 8 000 000 đồng.
Nếu trong một tháng nhân viên nào vượt chỉ tiêu thì được thưởng thêm 8% tiền lời của số xe được bán vượt chỉ tiêu đó. Trong tháng 5 (có 31 ngày), anh Thành nhận được số tiền là 9 800 000 đồng (bao gồm cả lương cơ bản và tiền thưởng thêm tháng đó). Hỏi anh Thành đã bán được bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe máy bán ra thì cửa hàng thu lời được 2 500 000 đồng.
Theo quy định của cửa hàng xe máy, đề hoàn thành chỉ tiêu trong một tháng, mỗi nhân viên phải bán được trung bình một chiếc xe máy trong một ngày. Nhân viên nào hoàn thành chỉ tiêu trong một tháng thì nhận lương cơ bản là 8 000 000 đồng.
Nếu trong một tháng nhân viên nào vượt chỉ tiêu thì được thưởng thêm 8% tiền lời của số xe được bán vượt chỉ tiêu đó. Trong tháng 5 (có 31 ngày), anh Thành nhận được số tiền là 9 800 000 đồng (bao gồm cả lương cơ bản và tiền thưởng thêm tháng đó). Hỏi anh Thành đã bán được bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe máy bán ra thì cửa hàng thu lời được 2 500 000 đồng.
Quảng cáo
Trả lời:
Gọi \[x\] là số xe mà anh Thành bán được trong tháng 5.
Theo đề ta có phương trình
\[8\,000\,000 + \left( {x - 31} \right).8\% .2\,500\,000 = \,9800\,000\]
Giải phương trình trên ta được \[x = 40\].
Vậy anh Thành bán được 40 chiếc xe máy trong tháng 5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
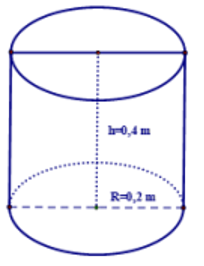
a) Thể tích 1 cái thùng hình trụ là
\[{V_{tru}} = \pi {R^2}h = \pi {.0,2^2}.0,4 \approx 0,05\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Lượng nước anh Minh đổ vào hồ trong mỗi lần gánh là
\[{V_g} = 2{V_{tru}}.90\% \approx 0,09\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Thể tích cái hồ là: \[V = 2.2.1 = 4\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có: \[4:0,09 \approx 44,44\]
Vậy anh Minh cần gánh ít nhất 45 lần để đầy hồ.
Lời giải

a)
Ta có:\[JM = JE\] (tính chất hai tiếp tuyến cắt nhau) và \[OM = OE\] (bán kính).
\[ \Rightarrow OJ\] là đường trung trực của \[ME\].
Từ đó suy ra \[\Delta OMJ = \Delta OEJ\] (c – c – c).
\[ \Rightarrow \widehat {MOF} = \widehat {EOF}\]
Từ đó suy ra \[\Delta OMF = \Delta OEF\] (c – g – c).
\[ \Rightarrow \widehat {OMF} = \widehat {OEF}\].
b)
Ta có \[\widehat {OMI} = \widehat {ODI} = 90^\circ \] (định nghĩa tiếp tuyến tại điểm).
Suy ra tứ giác \[ODIM\] nội tiếp (1).
Xét tam giác \[\Delta OED\] có \[\widehat {OED} = \widehat {ODE}\] (do \[OD = OE = R\])
Theo ý a) ta có \[\widehat {OMF} = \widehat {OEF}\] nên ta có \[\widehat {ODE} = \widehat {ODF} = \widehat {OMF}\]
Suy ra tứ giác \[ODMF\] nội tiếp (do cùng chắn cung \[OF\]) (2).
Từ (1) và (2) suy ra 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn.
c)
+) Ta có tứ giác\[IDOF\]nội tiếp (do 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn).
\[ \Rightarrow \widehat {DIO} = \widehat {DFO}\] (cùng chắn cung DO )
\[ \Rightarrow \widehat {AIO} = \widehat {EFO}\] (2 góc kề bù tương ứng) (3)
Ta lại có tứ giác \[ADOE\] nội tiếp (do \[\widehat {ADO} = \widehat {AEO} = 90^\circ \])
\[ \Rightarrow \widehat {DAO} = \widehat {DEO}\] (4)
Từ (3) và (4) suy ra (g – g).
\[ \Rightarrow \widehat {IOA} = \widehat {EOF}\]
Mà \[\widehat {EOF} = \widehat {JOM}\]
Nên \[\widehat {IOA} = \widehat {JOM}\].
+) Ta có \[\sin \widehat {IOA} = \sin \widehat {JOM} = \frac{{MJ}}{{OJ}}\] (5).
Mặt khác \[JMFO\] nội tiếp (do ý b) nên ta có \[\widehat {JMF} = \widehat {JOI}\].
Suy ra (g – g) \[ \Rightarrow \frac{{MJ}}{{JO}} = \frac{{MF}}{{OI}}\](6)
Từ (5) và (6) suy ra \[\sin \widehat {IOA} = \frac{{MF}}{{IO}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.