Quy tắc sau đây cho ta biết CAN, CHI của năm \[X\] nào đó.
Để xác định CAN, ta tìm số dư \[r\] trong phép chia \[X\] cho 10 và tra vào bảng 1.
Để xác định CHI, ta tìm số dư \[s\] trong phép chia \[X\] cho 12 và tra vào bảng 2.
Ví dụ: năm 2020 có CAN là Canh, CHI là Tí.
Bảng 1
\[r\]
0
1
2
3
4
5
6
7
8
9
CAN
Canh
Tân
Nhâm
Quý
Giáp
Ất
Bính
Đinh
Mậu
Kỷ
Bảng 2
\[s\]
0
1
2
3
4
5
6
7
8
9
10
11
CHI
Thân
Dậu
Tuất
Hợi
Tí
Sửu
Dần
Mẹo
Thìn
Tỵ
Ngọ
Mùi
a) Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm 2005?
b) Bạn Hằng nhớ rằng Nguyễn Huệ lên ngôi hoàng đế, hiệu là Quang Trung vào năm Mậu Thân nhưng không nhớ rõ đó là năm bao nhiêu mà chỉ nhớ là sự kiện trên xảy ra vào cuối thế kỉ 18. Em hãy giúp Hằng xác định chính xác năm đó là năm bao nhiêu?
Quy tắc sau đây cho ta biết CAN, CHI của năm \[X\] nào đó.
Để xác định CAN, ta tìm số dư \[r\] trong phép chia \[X\] cho 10 và tra vào bảng 1.
Để xác định CHI, ta tìm số dư \[s\] trong phép chia \[X\] cho 12 và tra vào bảng 2.
Ví dụ: năm 2020 có CAN là Canh, CHI là Tí.
Bảng 1
|
\[r\] |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
CAN |
Canh |
Tân |
Nhâm |
Quý |
Giáp |
Ất |
Bính |
Đinh |
Mậu |
Kỷ |
Bảng 2
|
\[s\] |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
CHI |
Thân |
Dậu |
Tuất |
Hợi |
Tí |
Sửu |
Dần |
Mẹo |
Thìn |
Tỵ |
Ngọ |
Mùi |
a) Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm 2005?
b) Bạn Hằng nhớ rằng Nguyễn Huệ lên ngôi hoàng đế, hiệu là Quang Trung vào năm Mậu Thân nhưng không nhớ rõ đó là năm bao nhiêu mà chỉ nhớ là sự kiện trên xảy ra vào cuối thế kỉ 18. Em hãy giúp Hằng xác định chính xác năm đó là năm bao nhiêu?
Quảng cáo
Trả lời:
a) Ta có:
2005 : 10 = 200 dư 5 Þ CAN = “ẤT”.
2005 : 12 = 167 dư 1 Þ CHI = “DẬU”.
Vậy năm 2005 có CAN là “Ất”, CHI là “Dậu”.
b) Gọi \[x\] là năm Nguyễn Huệ lên ngôi hoàng đế \[\left( {x \in \mathbb{N}} \right)\].
Do \[x\] thuộc cuối thế kỉ 18 nên \[1750 \le x \le 1799\].
Do CAN của \[x\] là Mậu nên \[x\] : 10 dư 8.
Suy ra hàng đơn vị của \[x\] là số 8.
Suy ra \[x\] là một trong các năm 1758, 1768, 1778, 1788, 1798.
Do CHI của \[x\] là “Thân” nên \[x\] chia hết cho 12.
Vậy chỉ có năm 1788 thỏa mãn.
Vậy Nguyễn Huệ lên ngôi hoàng đế năm 1788.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
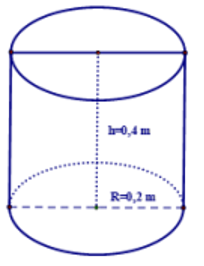
a) Thể tích 1 cái thùng hình trụ là
\[{V_{tru}} = \pi {R^2}h = \pi {.0,2^2}.0,4 \approx 0,05\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Lượng nước anh Minh đổ vào hồ trong mỗi lần gánh là
\[{V_g} = 2{V_{tru}}.90\% \approx 0,09\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Thể tích cái hồ là: \[V = 2.2.1 = 4\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\]
Ta có: \[4:0,09 \approx 44,44\]
Vậy anh Minh cần gánh ít nhất 45 lần để đầy hồ.
Lời giải

a)
Ta có:\[JM = JE\] (tính chất hai tiếp tuyến cắt nhau) và \[OM = OE\] (bán kính).
\[ \Rightarrow OJ\] là đường trung trực của \[ME\].
Từ đó suy ra \[\Delta OMJ = \Delta OEJ\] (c – c – c).
\[ \Rightarrow \widehat {MOF} = \widehat {EOF}\]
Từ đó suy ra \[\Delta OMF = \Delta OEF\] (c – g – c).
\[ \Rightarrow \widehat {OMF} = \widehat {OEF}\].
b)
Ta có \[\widehat {OMI} = \widehat {ODI} = 90^\circ \] (định nghĩa tiếp tuyến tại điểm).
Suy ra tứ giác \[ODIM\] nội tiếp (1).
Xét tam giác \[\Delta OED\] có \[\widehat {OED} = \widehat {ODE}\] (do \[OD = OE = R\])
Theo ý a) ta có \[\widehat {OMF} = \widehat {OEF}\] nên ta có \[\widehat {ODE} = \widehat {ODF} = \widehat {OMF}\]
Suy ra tứ giác \[ODMF\] nội tiếp (do cùng chắn cung \[OF\]) (2).
Từ (1) và (2) suy ra 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn.
c)
+) Ta có tứ giác\[IDOF\]nội tiếp (do 5 điểm \[I;\,D;\,O;\,F;\,M\]cùng nằm trên một đường tròn).
\[ \Rightarrow \widehat {DIO} = \widehat {DFO}\] (cùng chắn cung DO )
\[ \Rightarrow \widehat {AIO} = \widehat {EFO}\] (2 góc kề bù tương ứng) (3)
Ta lại có tứ giác \[ADOE\] nội tiếp (do \[\widehat {ADO} = \widehat {AEO} = 90^\circ \])
\[ \Rightarrow \widehat {DAO} = \widehat {DEO}\] (4)
Từ (3) và (4) suy ra (g – g).
\[ \Rightarrow \widehat {IOA} = \widehat {EOF}\]
Mà \[\widehat {EOF} = \widehat {JOM}\]
Nên \[\widehat {IOA} = \widehat {JOM}\].
+) Ta có \[\sin \widehat {IOA} = \sin \widehat {JOM} = \frac{{MJ}}{{OJ}}\] (5).
Mặt khác \[JMFO\] nội tiếp (do ý b) nên ta có \[\widehat {JMF} = \widehat {JOI}\].
Suy ra (g – g) \[ \Rightarrow \frac{{MJ}}{{JO}} = \frac{{MF}}{{OI}}\](6)
Từ (5) và (6) suy ra \[\sin \widehat {IOA} = \frac{{MF}}{{IO}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.